垂直抗力
正常な力とは、地面（またはあらゆる面）が押し返す力のことです。正常な力がなかったら、ゆっくりと地面に染み込んでいることになります。
物体にかかる法線力は、物体が乗っている面に対して常に垂直（直角）になっています。
平らな面上では 物体の法線力は
物体の重さ、つまり質量に重力を掛けたもの）。
傾斜面上では、角度によって法線力が減少し、法線力は
.
平らな面では θ {\displaystyle \theta
} は０になるので、θ {\displaystyle coshe\ta
} は１になる。２つの式は等しくなる。
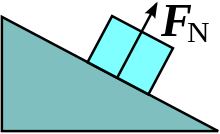
FNは 法線力を 表します。
質問と回答
Q:法線力とは何ですか?
A: 法線力とは、地面（または任意の表面）が押し返す力のことです。
Q: もし法線力がなかったらどうなるのでしょうか?
A: 法線力がなかったら、あなたはゆっくりと地面にしみこんでいくでしょう。
Q: 物体にかかる法線力は、その重量とどのように関係しているのでしょうか?
A: 平らな面では、物体の法線力はその重量（物体の質量に重力の力を掛けたもの）に等しくなります。
Q: 傾斜面は法線力にどのような影響を与えるのでしょうか?
A: 傾斜面では、法線力は角度によって減少し、m g c o s θ で計算することができます。
Q: この式でθは何を表しているのか?
A: θはこの式の傾斜角度を表しています。
Q: cosθが1になるのはどんなときか?
A: cosθが1になるのは、θ（角度）が0のときで、これは平らな面で起こります。
Q: この2つの方程式は、互いにどのように比較されるのか?A: 平面上では2つの方程式は等しくなります。
