スネルの法則
スネルの屈折の法則とは、光や他の波の屈折に関する科学的な法則です。光学では、スネルの法則は、異なる媒体での光の速度についてです。この法則では、光が異なる物質（例えば空気からガラスへ）を通過しても、入射角（入射角）と屈折角（出射角）のサインの比は変わらないとされています。
sin θ 1 sin θ 2 = v 1 v 2 = n 2 n 1 {\display style {\ style {Votha _{1}}{\sin \theta _{2}}}={V_{1}}{V_{2}}}={V_{1}}{V_{2}}}={V_{1}}}} 
θを境界の法線からの角度、
vを媒質中の光の速度（SI単位はm/s）とし、
nを媒質の屈折率とする。 
真空の屈折率を１、真空中の光の速度をｃ {\displaystyle c
} 。屈折率がnの物質を波が通過するとき、波の速度はc n {\displaystyle {frac {c}{n}}}になる。
.
スネルの法則はフェルマーの原理で証明できる。フェルマーの原理は 光は最も時間のかからない経路に沿って移動すると述べています
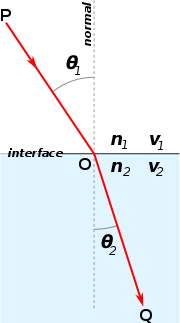
屈折率の異なる2つの媒体の界面での光の屈折率、n2 > n1
光線がガラスのプリズムに当たって屈折する
歴史
この考え方には長い歴史があります。この問題はアレクサンドリアの英雄、プトレマイオス、イブン・サール、ホイヘンスの注目を集めていました。イブン・サールは実際に屈折の法則を発見しました。ホイヘンスは、1678年の『Traité de la Lumiere』の中で、スネルのサインの法則が光の波動性によって説明できることを示しました。
質問と回答
Q: スネルの屈折法則とは何ですか?
A: スネルの屈折法則とは、光やその他の波の屈折に関する科学的法則のことです。光学の分野では、光が異なる物質を通過するとき、入射角と屈折角の正弦の比が変化しないことを述べています。
Q: スネルの法則はどのように証明できるのですか?
A: スネルの法則は、「光は最も時間のかからない経路を通る」というフェルマーの原理によって証明することができます。
Q: フェルマーの原理とは何ですか?
A:フェルマーの原理とは、「光は最も時間のかからない経路を通る」というものです。
Q: スネルの法則のnとvは何ですか?
A: nは媒質の屈折率、vは媒質中の光の速度（単位はメートル毎秒）です。
Q: スネルの法則でcは何を表しているのか?
A: cは、屈折率が1に等しい真空中の光速を表します。
Q: 波が屈折率nの物質を通過するときの速度はどのように計算するのですか?
A: 波が屈折率nの物質を通過するとき、速度はc/nになります。
