Theorema Egregium（ガウスの注目すべき定理）—曲面のガウス曲率と不変性
ガウスのTheorema Egregium（ラテン語で「注目すべき定理」の意）は、カール・フリードリヒ・ガウスが証明した微分幾何学の主要な結果である。この定理は、曲面の曲率に関するものです。この定理では、曲率は表面上の角度、距離、その割合を測定するだけで決定できるとしている。曲面が周囲の3次元ユークリッド空間にどのように埋め込まれているかについては、特に語る必要はない。つまり、曲面を伸ばさずに曲げても、ガウス曲率は変わらないのである。
ガウスは、この定理をこのように提示した（ラテン語からの翻訳）。
このような理由から、前の記事の公式は、それ自体で驚くべき定理を導く。ある曲面を他のどんな曲面の上に展開しても、各点における曲率の測定値は変わらない。
この定理が「注目に値する」のは、ガウス曲率の出発点となる定義が、空間における曲面の位置を直接利用しているからである。そのため、曲げやねじりの変形を受けたにもかかわらず、その結果が埋め込みに依存しないことは非常に驚くべきことです。
定義と直感
ガウス曲率（Gaussian curvature）は、点における曲面の局所的な「曲がり方」を表す量です。直感的には、その点での法線方向周りに顔を回したときに曲面がどのように曲がるかを示します。正の曲率は球面のようにあらゆる方向で同じ向きに曲がることを、負の曲率は鞍型のように異なる方向で反対向きに曲がることを意味します。曲率がゼロであれば、その点は平面的（例：円柱の側面の局所部分）とみなせます。
重要な点は、ガウスの定理によってガウス曲率は「内在的（intrinsic）」な量であると示されたことです。つまり、曲面上で長さや角度（第一基本形式）だけを使って測ることができ、曲面が3次元空間にどう埋め込まれているか（外在的な形）には依存しません。したがって、紙を伸ばさずに曲げる（巻く、ねじる）ような変形ではガウス曲率は変わりません。
数式的な表示（概略）
曲面の局所座標での第一基本形式の係数を E, F, G、第二基本形式の係数を L, M, N とすると、外面（埋め込み）から直接計算される式として
K = (L N − M^2) / (E G − F^2)
という式が知られています。ここでの L, M, N は法線方向の変化を表すため、一見すると曲面の埋め込みに依存するように見えます。しかしガウスは、実際にはこの K を第一基本形式 E, F, G とその導関数だけを用いて表現できることを示しました。つまり、E, F, G（すなわち曲面上の長さ・角度の情報）から K を完全に復元でき、埋め込みに関する情報は不要であるということです。
別の言い方をすると、ガウスは曲率が計量（metric）からのみ決まることを示したのです。計量は曲面上での長さや角度の情報を与えるもので、リーマン幾何学でいうところの内在的構造に相当します。
具体例と直観的な結果
- 平面：K = 0（全体として曲率がゼロ）。
- 円柱：局所的には平面と同じ計量を持つため K = 0（平面を曲げて作れる）。これが「紙を巻く」ことで曲率が変わらないことの典型例です。
- 球（半径 R）：K = 1 / R^2。球面は正の曲率を持ち、平面とは局所的にも大域的にも等しくできません（等距離・等角を保つ埋め込みは存在しない）。
これらの例からわかるように、平面と円柱は局所的に等しい（isometric）だが、球面と平面は等しくないという区別が生じます。地図投影の問題（球面を平面に等距離で写すことが不可能である）もこの性質の直接の帰結です。
応用と歴史的意義
Theorema Egregium は微分幾何学における根本的な転換点でした。古典的な視点（曲面の形は周囲の空間での埋め込みで決まる）に対し、ガウスは曲面自身の内在的性質だけで重要な幾何量が決まることを示しました。この考え方は後のリーマン幾何学や一般相対性理論（重力の記述に計量テンソルを用いる）などに大きな影響を与えました。
また、ガウスの仕事はその後の重要な定理群とも結びつきます。例えば、ガウス・ボネの定理（Gauss–Bonnet theorem）は曲面の全曲率と位相不変量（オイラー標数）を結びつけ、局所的な曲率情報が大域的なトポロジーに影響を与えることを示します。さらに、ボネやベルヌーイらによる曲面の剛性・存在定理（例：全曲率が与えられたときの埋め込み可能性に関する結果）もTheorema Egregium を基盤に発展しました。
まとめ（要点）
- Theorema Egregium はガウス曲率が曲面の内在的量であり、埋め込みに依存しないことを示した。
- 曲率は第一基本形式（計量）だけから計算でき、紙を伸ばさずに曲げる操作では不変である。
- この定理は地図作成、曲面の等長写像の可能性、リーマン幾何学といった広範な分野に重要な示唆を与えた。
参考までに、定理の直訳を示した先の一節はガウス自身の言葉の趣旨をよく伝えています。Theorema Egregium はまさにその名の通り、「注目すべき定理」として広く知られ続けています。
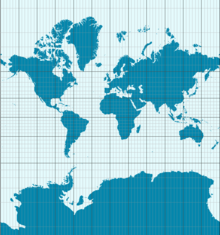
Theorema Egregiumの結果として、地球は歪まずに地図上に表示することができません。ここで紹介するメルカトル図法は、角度はそのままに面積を変えたものです。例えば、南極大陸は実際よりもずっと大きく表示されます。
質問と回答
Q: ガウスの『エグレギウム神学』とは何ですか?
A: ガウスの永遠性の定理は、カール・フリードリッヒ・ガウスによって証明された、曲面の曲率に関する微分幾何学の主要な結果です。
Q: どのようにして曲率が決まるのですか?
A: ガウスの永遠定理によれば、曲率は曲面上の角度、距離、およびそれらの割合を測定することによってのみ決定することができます。
Q: 曲率を決定するために、曲面が周囲の3次元ユークリッド空間にどのように埋め込まれるかについて話す必要がありますか?
A: いいえ、ガウスの永遠定理に従って曲率を決定するために、曲面が周囲の3次元ユークリッド空間に埋め込まれる特定の方法について話す必要はありません。
Q: 曲面を伸ばさないで曲げると、曲面のガウス曲率は変わるのですか?
A: いいえ、ガウスの永遠定理によれば、曲面を伸ばさないで曲げても曲面のガウス曲率は変わりません。
Q: 誰がこのような定理を示したのですか?
A: ガウスがこのような定理を示しました。
Q: この定理は何に注目すべきですか?
A: この定理が「注目に値する」のは、ガウスの曲率の定義が、空間における曲面の位置を直接利用しているからです。ですから、あらゆる曲げ変形やねじれ変形を受けたにもかかわらず、その結果が埋め込みに依存しないことは非常に驚くべきことなのです。
Q: ガウスはどのような方法で定理を提示したのですか?
A: ガウスは、曲面が他の曲面上に展開される場合、各点の曲率の尺度が変化しないような方法で定理を提示しました。
