計算化学
計算化学は、化学の一分野であり、化学的な問題を解決するためにコンピュータ科学を使用します。これらのプログラムは、分子や固体の構造や性質を計算します。計算化学は通常、化学実験で得られた情報を補完するものです。これは、まだ観測されていない化学現象を予測することができます。新薬や材料の設計に広く利用されています。
計算化学は、構造（分子の原子の予想される位置）、絶対・相対（相互作用）エネルギー、電子電荷分布、双極子や高次多極子モーメント、振動周波数、反応性や他の分光学的量、他の粒子との衝突のための断面積などを予測することができます。
計算化学は、静的なシステムと動的なシステムの両方を対象としています。いずれの場合も、研究対象となるシステムのサイズが大きくなると、コンピュータの時間やその他のリソース（メモリやディスクスペースなど）の使用量も大きくなります。このシステムは、単一の分子、分子群、固体のいずれであっても構いません。計算化学の手法には、高精度なものから非常に近似的なものまで様々なものがあります。高精度な方法は、通常、小さなシステムでのみ実現可能です。
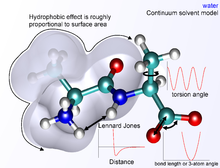
分子力学の潜在的なエネルギー関数で、Folding@Homeなどのプログラムで分子がどのように動き、どのように振る舞うかをシミュレートするために使用されます。
関連ページ
- バイオインフォマティクス
- 統計力学
質問と回答
Q:計算化学とは何ですか?
A: 計算化学は、化学的な問題を解決するためにコンピュータサイエンスを使用する化学の一分野です。分子や固体の構造や性質を計算し、まだ観測されていない化学現象を予測したり、新しい薬や材料を設計したりするのに利用されます。
Q:計算化学では、どのような系を見ているのですか?
A: 計算化学は、静的な系と動的な系の両方を対象としています。システムは、単一の分子、分子のグループ、または固体のいずれでもかまいません。
Q:計算化学はどのような情報を提供するのですか?
A: 計算化学は、構造（原子の位置）、絶対および相対エネルギー、電子電荷分布、双極子および高次多極子モーメント、振動数、反応性またはその他の分光学的量、および他の粒子との衝突の断面積といった情報を提供することができます。
Q:計算化学で使われる手法の精度はどのくらいですか?
A: 計算化学で使用される手法の精度は、高精度なものから非常に近似的なものまで様々です。高精度の手法は、一般的に小さな系でのみ実現可能です。
Q: 計算化学は、実験データをどのように補完するのですか?
A: 通常、計算化学は化学実験によって得られた情報を補完するものです。まだ実験的に観測されていない結果を予測するために使用することができます。
Q: 研究対象のシステムの大きさは、必要なコンピュータ時間に影響しますか?
A: はい。研究対象のシステムのサイズが大きくなればなるほど、解析に必要なコンピュータの時間や、保存に必要なメモリやディスクスペースなどの資源も大きくなります。
