相関とは(統計学)定義・正負の種類・測定法・因果関係との違い
相関の基本から種類・測定法、因果関係との違いまで図解でわかりやすく解説。正負の見分け方や実務で使えるポイントも。
統計学や確率論において、相関とは2つのデータセットがどれだけ密接に関係しているかを意味する。
相関関係は、必ずしも一方が他方を引き起こすことを意味するものではありません。第三の要因が絡んでいる可能性は大いにあります。
相関は通常、2つの方向のどちらかです。正または負である。正であれば、2つのセットは一緒に上昇する。負の場合は、一方が上昇し、他方が下降する。
相関関係については、さまざまな状況に応じて多くの異なる測定方法が用いられます。例えば、散布図では、相関の方向を示すために最良適合の線を描きます。
定義と基本的な性質
相関は「2変数間の結びつきの強さと向き」を示します。数値的には「相関係数(correlation coefficient)」で表され、多くの場合はピアソンの積率相関係数 r が使われます。r の値は -1 から +1 の範囲を取り、
- r = +1:完全な正の線形関係
- r = -1:完全な負の線形関係
- r = 0:線形相関がない(非線形な関係はあり得る)
ピアソンの相関係数は、共分散を各変数の標準偏差で割った値として定義されます(r = cov(X,Y) / (σ_X σ_Y))。
相関の種類(向きと強さ)
- 正の相関:片方が増えるともう片方も増える傾向。
- 負の相関:片方が増えるともう片方が減る傾向。
- 無相関:線形な結びつきが見られない(ただし非線形関係は存在するかもしれない)。
相関の強さは r の大きさで判断します。目安としては Cohen の基準がよく引用され、|r| ≈ 0.1(小)、≈ 0.3(中)、≈ 0.5(大)ですが、分野や目的に応じて実用的な解釈は異なります。
主な測定法と可視化
- ピアソン相関係数:線形関係を測る最も一般的な方法。連続変数・正規分布を仮定する場面でよく使われる。
- スピアマン順位相関(Spearman rho):順位に基づく相関。単調(monotonic)だが非線形な関係や外れ値に対して頑健。
- ケンドールの順位相関(Kendall's tau):順位の一致・不一致を使う別の順位相関係数で、小サンプルでも安定しやすい。
- 相関行列・ヒートマップ:多変量データで変数間の相関を一覧するのに便利。
- 散布図(scatter plot):まず視覚的に関係の有無・形状・外れ値を確認するのが重要。最良適合線(回帰直線)を描くと線形性の確認に役立つ。
統計的検定と信頼性
相関係数の有意性は検定によって評価できます。ピアソンの r の場合、帰無仮説「真の相関がゼロ」に対して t 検定を用いることが多く、標本サイズ n が小さいと推定の不確かさが大きくなります。信頼区間や p 値を併せて報告すると解釈が明確になります。
注意すべき前提:ピアソン相関の推論には通常、線形性・等分散性(等分散)・正規性(特に小標本での検定)などの仮定が関わります。これらが満たされない場合はスピアマンなどの順位法やデータ変換を検討してください。
相関と因果関係の違い(よくある誤解)
重要:相関は因果関係を示さない。相関が見られても、次のいずれかの可能性があるだけです。
- X が Y を引き起こす(因果)
- Y が X を引き起こす(逆因果)
- 第三の変数 Z が X と Y の両方に影響している(交絡)
- 偶然や測定誤差・サンプリングバイアスによる見かけの相関(偽相関)
有名な例として「アイスクリーム消費量と溺死者数に正の相関がある」ことがありますが、これは暑さ(共通の原因)が両方を増加させるための偽相関です。また、シンプソンのパラドックスのように、集計方法次第で相関の方向が変わることもあります。
因果推論に向けた手法(相関から一歩進む)
- ランダム化比較試験(RCT):因果を確立する最も強い方法。
- 操作変数法(Instrumental Variables):交絡がある場合に有効な手法。
- 回帰による調整・部分相関:既知の交絡因子を統制して残差同士の相関を見る。
- 時系列データでは Granger 因果性検定:予測情報の観点から因果の可能性を評価。
- 因果推論フレームワーク(潜在変数モデル、差分の差分、傾向スコア法など)
実務的なアドバイス
- まずは散布図でデータを可視化し、外れ値や非線形性を確認する。
- 目的に応じて適切な相関指標を選ぶ(ピアソン vs スピアマン vs ケンドール)。
- 相関の強さだけで結論を出さず、統計的有意性(p 値・信頼区間)と実務上の意味を両方考慮する。
- 因果関係を主張するには追加の設計(RCT や適切な観察データ分析)や理論的根拠が必要。
- 複数の変数を扱う場合は相関行列や回帰分析、部分相関分析で交絡の可能性を検討する。
まとめ
相関は変数間の「結びつき」を量的に表す重要な指標ですが、因果関係とは別概念です。測定法(ピアソン・スピアマン・ケンドール)や可視化を使って関係の性質を正しく把握し、必要なら因果推論の手法を用いて慎重に解釈してください。
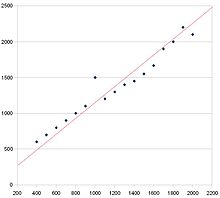
この散布図には正の相関があります。トレンドが右肩上がりなのでわかります。赤い線は最良適合線です。
相関関係を説明する
強いとか弱いとかいうのは、相関関係を表す言葉です。強い相関がある場合は、ポイントがすべて接近しています。相関が弱い場合は、ポイントがばらばらになっています。相関の強さを数値で表す方法があります。これらの測定値は相関係数と呼ばれます。最もよく知られているのは、ピアソン積率相関係数です。データを計算式に入れると、数値が出ます。その数値が1または-1であれば、強い相関があることになります。もし答えが0なら、相関はありません。相関係数のもう一つの種類は、スピアマンの順位相関係数です。
相関関係 vs 因果関係
相関関係は、あることが他のことを引き起こすとは限らない(因果関係)。なぜなら、何か他のことが両方の原因になっているかもしれないからだ。例えば、暑い日に人々はアイスクリームを買い、また、人々はビーチに行き、そこでサメに食べられる人もいます。アイスクリームの売り上げとサメの攻撃には相関関係があります(この場合、気温が上がると両方が上がります)。しかし、アイスクリームの売り上げが上がったからといって、アイスクリームの売り上げが原因で(因果関係)サメの襲撃が増えるわけでもなく、その逆もまた然りである。
相関関係は因果関係を意味しないので、科学者や経済学者などは、1つの要因だけを変化させる隔離された環境を作って(それが可能な場合)、自分たちの理論を検証する。しかし、政治家、セールスマン、報道関係者などは、しばしば特定の相関関係が因果関係を示唆するようなことを言います。これは、無知であったり、説得したいがためであったりする。例えば、ある商品をより多く消費している人は、ある健康問題を抱えていると報道することで、注目を集め、実際には他の要因によるものかもしれない因果関係を暗に示すことがある。
関連ページ
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003).行動科学のための応用重回帰分析/相関分析.(第3版) Hillsdale, NJ: Lawrence Erlbaum Associates.
質問と回答
Q: 相関とは何ですか?
A: 相関とは、2つのデータセットがどれだけ密接に関連しているかを示す方法です。
Q: 相関とは、一方のデータが他方のデータを引き起こすということですか?
A: いいえ、相関は常に一方のデータが他方のデータを引き起こすことを意味するわけではありません。実際には、第三の要因が関与していることが多い。
Q: 相関の2つの方向とは何ですか?
A: 相関の2つの方向は正と負です。
Q: 正の相関とはどういう意味ですか?
A: 正相関とは、2つのデータセットが共に上昇することを意味する。
Q: 負の相関とはどういう意味ですか?
A: 負の相関とは、一方のデータが上昇し、他方のデータが下降することを意味します。
Q: 相関にはさまざまな測定方法がありますか?
A: はい、さまざまな状況に応じて、さまざまな相関の測定が行われています。
Q: 散布図では相関の方向をどのように表すことが多いですか?
A: 散布図に相関の方向を示すために,最良適合線を引くことがよくある.
百科事典を検索する