オイラー・ベルヌーイの梁理論とは？定義・式・応用例をわかりやすく解説

オイラー・ベルヌーイ梁理論の定義・基本式・実践的応用を図解でわかりやすく解説。初心者から実務者まで設計・解析に役立つ入門ガイド。

オイラー・ベルヌーイの梁理論（エンジニアの梁理論、古典的な梁理論とも呼ばれる）は、荷重をかけたときの梁の曲げを計算する簡単な方法である。これは、せん断変形の影響を考慮することなく、梁の小さなたわみ（何かがどれだけ動くか）に適用される。そのため、ティモシェンコの梁理論の特殊なケースともいえる。最初に紹介されたのは1750年頃。1750年頃に登場し、19世紀末のエッフェル塔や観覧車の開発で注目を集めた。その後、機械工学や土木工学など多くの工学分野で用いられてきた。他の先進的な手法も開発されているが、オイラー・ベルヌーイの梁理論は、そのシンプルさゆえに今でも広く使われている。 

定義と基本的な仮定

オイラー・ベルヌーイ梁理論は、以下のような仮定に基づく古典的な線形弾性理論です。

• 小変形仮定：たわみが小さく、幾何学的非線形性を無視できる。
• 断面は平面のまま：梁の任意断面は曲げ後も平面を保ち、曲げ中心に対して常に直交する（断面がねじれない）。
• せん断変形を無視：せん断による変形は無視され、曲げによる曲率のみでたわみが支配される。
• 材料は線形弾性で等方的：フックの法則が成り立ち、ヤング率 E や断面二次モーメント I は既知。

基本式（支配方程式と曲げ-曲率関係）

代表的な支配方程式は分布荷重 q(x) が作用する場合の4階常微分方程式です：

EI d^4w/dx^4 = q(x)

ここで w(x) は梁の垂直たわみ、E はヤング率、I は断面二次モーメントです。

曲げモーメント M(x) とたわみの二階微分（曲率に比例）の関係は：

M(x) = - E I d^2w/dx^2

（符号規約は文献により異なりますが、符号よりも関係式の意味 ─ 曲げモーメントが曲率を生む ─ を重視します。）

境界条件と解法の流れ

支配方程式は4次なので、境界条件が4つ必要です。典型的な境界条件の種類：

• 支持点でのたわみ w = 0（例：単純支持、固定支持）
• 勾配（回転） dw/dx = 0（例：固定端の回転拘束）
• せん断力 V = dM/dx の指定
• 曲げモーメント M の指定

解法の流れは、作用荷重（集中荷重や分布荷重）を与えて、静力学的平衡でせん断力・曲げモーメントの分布を求め、そこから上の関係式を用いてたわみ方程式を積分していきます。必要に応じ定数は境界条件で決定します。

代表的な解（よく使われる公式）

いくつかの標準ケースの最大たわみ（線形理論による）を示します。以下はよく使われる簡潔な公式です。

• 片持ち梁（自由端に集中荷重 P、根元に固定、梁長 L）：自由端のたわみ δ = P L^3 / (3 E I)
• 単純支持梁（一点集中荷重 P が中央に、支点間距離 L）：中央最大たわみ δ = P L^3 / (48 E I)
• 単純支持梁（等分布荷重 q_0）：最大たわみ δ_max = 5 q_0 L^4 / (384 E I)

（これらは符号や荷重位置により異なるので、設計では問題設定を正確に確認してください。）

応用例

• 橋梁や建築物の梁・桁のたわみ計算
• クレーンブームや船舶のマストなどの曲げ評価
• 機械部品（シャフト、アーム）の変形と応力評価
• 構造の初期設計段階での概算（早期の手計算や教科書的参照）

利点と限界（いつ使えるか／使えないか）

利点：理論が単純で解析解が得やすく、設計・教育・概算に非常に有用です。

限界：

• せん断変形が無視されるので、厚い（短い）梁や高せん断の問題では誤差が大きくなる（その場合はティモシェンコ梁理論を使う）。
• 大変形（幾何学的非線形）や材料の非線形（塑性、複合材料など）には適用できない。
• ねじりや複雑な断面効果、断面の非均質性が重要な場合は拡張モデルや有限要素法が必要。

実務上の注意点

• 設計では、安全率や許容たわみの基準（例えば建築基準や使用上の許容値）を確認する。
• 実験や有限要素解析（FEA）と組み合わせて、オイラー・ベルヌーイ理論の適用範囲内であることを確認する。
• 動的問題（振動、衝撃）では回転慣性やせん断変形が影響することがあり、より厳密なモデルが必要。

まとめ

オイラー・ベルヌーイの梁理論は、簡潔で扱いやすい古典理論として、たわみや曲げ応力の初期評価に広く使われています。基本仮定を理解し、適用範囲（小ひずみ・せん断が無視できる場合）を守れば、設計や解析に役立つ有力な手法です。より精密な解析が必要な場合は、ティモシェンコ理論や有限要素法などの手法を併用してください。

沿革

1750年にレオンハルト・オイラーとダニエル・ベルヌーイが初めて理論をまとめました。当時は、科学や工学に対する考え方が今とは違っていました。オイラー・ベルヌーイの梁理論のような数学的理論は、実用的な工学としては信用されていなかったのである。橋や建物の設計は、19世紀後半まで同じ方法で行われていた。エッフェル塔や観覧車が、理論の有効性をより大きなスケールで示したのはこの時です。

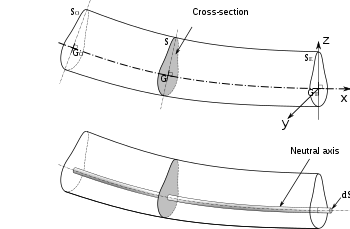
中立軸を示す屈曲したビームの断面図

静的ビーム方程式

梁のたわみと荷重の関係を表すオイラー・ベルヌーイ方程式は次のようになります。

d 2 d x 2 ( E I d 2 w d x 2 ) = q {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}^{2}}{\\{d} x^{2}}}left(EI{\\\{d} ^{2}w}{\\{d} x^{2}}}right)=q\,}。

ここで、w ( x ) {\displaystyle w(x)}は、ある位置x {\displaystyle x}でのz {\displaystyle z}方向の梁のたわみを表す。 q {\displaystyle q}は、分布荷重、つまり単位長さあたりの力（圧力が面積あたりの力であるのと似ている）であり、x {\displaystyle x} 、w {\displaystyle w} 、または他の変数の関数であり得る。その他の変数の関数である。

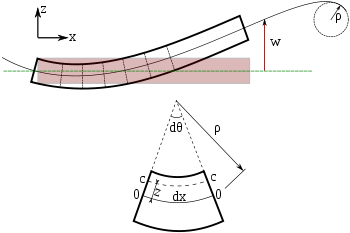
オイラー・ベルヌーイビームの曲げ加工。梁の各断面は中立軸に対して90度である。

質問と回答

Q: オイラー・ベルヌーイビーム理論とは何ですか?

Q: オイラー・ベルヌーイ梁理論はいつから導入されたのですか?

Q:エッフェル塔や観覧車の開発にはオイラーベルヌーイ梁理論が使われたのでしょうか?

Q:オイラー・ベルヌーイ梁理論が使われている工学分野にはどのようなものがありますか?

Q:オイラーベルヌーイ梁理論は現在も広く使われているのでしょうか?

Q: オイラー・ベルヌーイ梁理論は、どのような梁のたわみに適用されるのですか?

Q: オイラーベルヌーイ梁理論は、せん断変形の影響を考慮するのでしょうか?

文字で検索