不等式の定義と記号解説：<, >, ≤, ≥ の意味と使い方

不等式(<, >, ≤, ≥)の意味と使い方を図解と例でわかりやすく解説。記号の読み方・等号との違い・応用問題つきで数学初心者や復習に最適。

著者: Leandro Alegsa

31-01-2026 18:44

不等号の基本と読み方

不等号（ふとうごう）は、二つの数や式の大小関係を表す記号です。主に次の4つが使われます。読み方と意味をわかりやすく説明します。

<（小なり）：a < b は「a は b より小さい」を意味します。例：2 < 5 は「2 は 5 より小さい」。 $\ a<b$
>（大なり）：a > b は「a は b より大きい」を意味します。例：7 > 3 は「7 は 3 より大きい」。 $\ a>b$
≥（以上）：a ≥ b は「a は b より小さくない」、すなわち「a は b と等しいか、または b より大きい」を意味します。例：5 ≥ 3 は真、3 ≥ 3 も真です。 $a\geq b$ （a は b より小さくない、つまり a は b と等しいか大きい） equal
≤（以下）：a ≤ b は「a は b より大きくない」、すなわち「a は b と等しいか、または b より小さい」を意味します。例：2 ≤ 4 は真、4 ≤ 4 も真です。 $a\leq b$

不等式の性質と使い方（基礎）

推移性（transitive）：もし a < b かつ b < c ならば a < c。非厳密でも、a ≤ b かつ b ≤ c なら a ≤ c です。
同じ数を足したり引いたりする：任意の数 c に対して、a < b なら a + c < b + c（等号付きも同様）。大小関係は変わりません。
正の数で掛ける：c > 0 のとき、a < b なら ac < bc（等号付きは ≤ に置換可）。
負の数で掛ける（向きが逆になる）：c < 0 のときは不等号の向きが反転します。つまり a < b なら ac > bc となります。これは多くの誤りの原因になるので注意してください。
両辺を0で割ることはできない：0 で割ることは定義されていないため、代わりに不等式を変形する際は掛け算・割り算の符号に注意してください。

不等式の表し方（区間）と読み方の例

a < x < b：x は a と b の間にあり、両端は含まない（開区間 (a, b)）。
a ≤ x ≤ b：x は a と b の間にあり、両端を含む（閉区間 [a, b]）。
例：-1 < x ≤ 2 は「x は -1 より大きく、かつ 2 以下」。

よくある注意点と間違いやすい点

不等号を反転させる条件：両辺に負の数を掛ける（または負の数で割る）ときは不等号が逆向きになります。例えば -2x < 6 を x について解くとき、両辺を -2 で割ると x > -3 になります（向きが変わる）。
等号と不等号の違い：a < b は a と b が等しくないことを意味しますが、a ≤ b は a = b の可能性も含みます。
文字式の扱い：不等式を変形するときは常に掛け算・除算で符号が変わらないか確認してください。平方や二乗根を含む場合も注意が必要です。

不等式は、「一方の式や数が他方より小さい・大きい・小さくない・大きくない」といった関係を簡潔に表すために使われます。基本ルールと注意点をおさえれば、方程式と同様に扱って解くことができます。

不平等との協働

数学の不等式とは、2つの解や答えが比較されるときに、より大きいかより小さいかで比較されることです。それは、比較されている2つまたはまだ多くのソリューションが等しい量ではないときです。不等式を解くことは、その解を見つけることを意味します。変数に数値を代入して、その文が真であれば、それは解です。数を変数に代入して、その文が真でない場合、その数はその文の解ではありません。

不等式とは、与えられた変数の解を見つけることです。これは、集合の相対的な順序を見つけることです。不等式には多くの解がありますが、実数の解を見つける必要があります。不等式は実数を解くことです。不等式の正しい読み方は、他の方程式と同じように左から右へと読みますが、唯一の違いは、方程式ごとに異なるルールを持っていることです。

例えば、x+4>12、ここでxは実数である。まず、人はxを求めて、それが解であるかどうかを知る必要があります。答えはx>8となり、真の式となります。この式は、実数の集合内でのxの位置についての式です。他のすべての実数との相対的な位置関係を示す方法として、数直線があります。図の不等式1を参照してください。

不等式1 これは、x+4>12の方程式の解です。

異なる種類の不平等

不等号の種類は5種類。

1つ目は線形不等式で、式を小さいか等しくないか、小さいか等しくないか、大きいか等しくないか、大きいか等しくないかのどちらかで微分する不等式です。これを等式関係の不等式に置き換えると、結果は一次方程式になるというものです。
2つ目は、不等式を満たすための不等式の組み合わせで、不等式を満たす数が2つの解セットの交点の値になるように、解セットに数を持っている必要があります。
3つ目は、絶対値を含む不等式で、絶対値を含む不等式の組み合わせとして言い換えることができます。
4番目のものは多項式不等式と呼ばれ、それが連続的であることを意味し、それは彼らのグラフがジャンプや休憩を持っていないことを意味します。
最後に、有理不等式、つまり、多項式を多項式で割ったものを一つの形にしたものです。つまり、有理関数グラフには改行はなく、分母のゼロ点で表すこともありません。

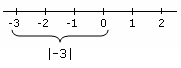
絶対値絶対値を示す例

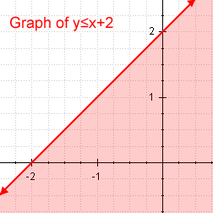
線形不等式線形不等式の例

不等式を解く4つの方法

二次方程式の解き方は4つあります。

ルールその１は、両面で同じ数を足したり引いたりしなければならないということです。
ルールその2は、サイドをずらして不等号の位置を変えることです。
3番のルールは掛け算をすることだ
ルール4番は、同じ正負の数を両辺で割ることです。ただし、これは簡単な不等式の問題にしか使えません。

さらに、不等式を解くには2つのステップを踏むことになります。1つ目は、足し算や引き算の逆数を使って単純化すること。2つ目は、掛け算や割り算の逆数を使ってさらに単純化することです。不等式を負の数で掛けたり割ったりするときは、不等式の記号を回すことを忘れないようにしましょう。

不等式の掛け算の例

不等式を足した例。

不等式の解き方の例

不等式とは、2つの値が等しくないことを説明する数学的な記述です。不等式はどんな式でも同じですが、唯一の違いは、不等式は等号を使わない代わりに記号を使うことです。不等式のb>aは、bがaより大きいことを表しています。

不等式を解くとき、人は真の文を持つ必要があります。負の数で不等式を割ったり掛けたりするとき、その文は偽です。数字が正の数の場合は、記号を逆にする必要はありません。不等式とは、真の文を作ることです。

例えば、-6y<-12という真の文から始めます。この文では、y>2が正解となるように、記号を逆にする必要があります。数列（図2の不等式参照）の中で、閉じた斜線の円は、解の集合に含まれていることを示しています。開いた円は、解の集合に含まれないことを示しています。

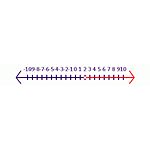
不等式 2 方程式の解 -6y<-12

質問と回答

Q:「a＜b」とはどういう意味ですか?

A:aがbより小さいという意味です。

Q:「a＞b」とはどういう意味ですか?

A:aがbより大きいという意味です。

Q:「a≧b」とはどういう意味ですか?

A:「aはbより小さくない、つまり、bより大きいか等しい」という意味。

Q:「a≦b」とはどういう意味ですか?

A:「aはbより大きくない、またはbより小さいか等しい」という意味です。

Q:不等式は数学でどのように使われるのですか?

A:不等式は、ある式が他の式より小さい、大きい、小さくない、大きくないという命名に使うことができます。

百科事典を検索する