光時計とは|相対性理論で示す時間拡張の原理と数学的導出
光時計で理解する相対性理論の時間拡張。直感的な例と代数・ピタゴラスの定理による数学的導出を図解で丁寧に解説。
光時計は、特殊相対性理論における「時間の遅れ(時間拡張)」を直感的かつ数学的に示す代表的な思考実験です。光時計は、ポールの下端で光を発し、上端に置かれた鏡で反射して戻ってくる光の往復を「1ティック」と数えるように作られています。光の往復回数をカウントすることで時間を測るこの単純な装置を、地上にいる観測者が上空を高速で通過する宇宙船内に持っていると仮定すると、地上の観測者は宇宙船内の時計がゆっくり刻むように見える(時間が伸びる)ことがわかります。これが時間拡張の基本的な説明です(専門用語では「動いている時計は遅れる」)。
まずは直感的な例:ドリブルするバスケットボール
比較のために、飛行機の中で選手がバスケットボールをドリブルしている光景を考えます。機内の乗客にとってはボールは上下に1回バウンドするごとに約1秒の周期で動きますが、地上から見ると飛行機ごと移動しているためバウンド間にボールは前方へ移動しています。この運動の違いが見かけ上の挙動を変えるのと同様に、光時計でも「光の経路が斜めになる」ことが時間に違いを生みます。
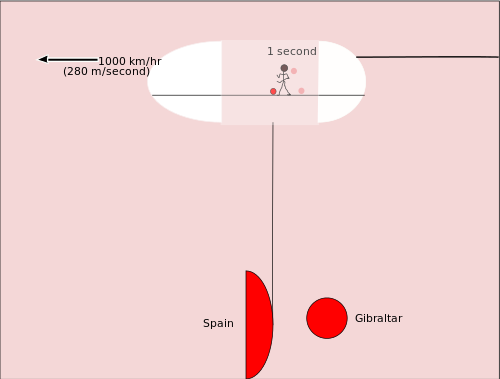
光時計の幾何学的モデルと変数の定義
ここで、光の速さを c、宇宙船(光時計)が地球に対して移動する速さを r(=v と同義と考えてください)、ポールの長さ(鏡と発光点の垂直距離)を a、地上の観測者が見る「一回の往復(1ティック)に要する時間」を t'、光時計自身(時計が静止している系)で測る往復時間(固有周期)を t とします。
光時計が静止している系(時計の固有系)では、光は垂直に上がって下がるだけなので、往復に要する時間(固有時間)は
t = 2a / c
です。これがいわゆる「固有時間(proper time)」で、時計に貼りついた観測者が直接測る時間です。
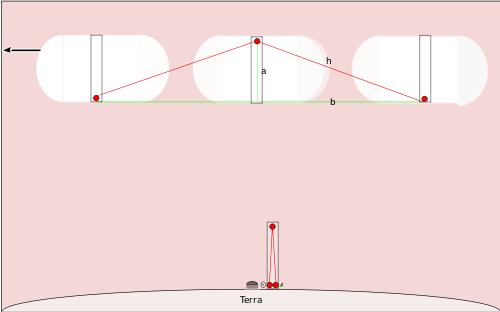
地上の観測者から見た光の経路(斜めの経路)
地上の観測者から見ると、光束は鏡に向かって斜め上に進み、鏡から戻るときは斜め下に進みます。往復のうち上向き半分(片道)を考えると、光が片道に移動する間に宇宙船は距離 (r t' / 2) だけ進みます。このとき光の片道の経路の長さ h はピタゴラスの定理から
h = √( a² + (r t' / 2)² )
往復(上向き+下向き)で光が進む距離は d = 2h となり、光速は常に c なので地上の観測者が測る往復時間 t' に対して次が成り立ちます:
c t' = 2 √( a² + (r t' / 2)² )
方程式の解法(時間拡張の導出)
上式を t' について解きます。以下は主要な代数操作の流れです(簡潔に):
- 両辺を二乗して、(c t')² = 4 ( a² + (r t' / 2)² )
- 右辺を展開すると (c t')² = 4 a² + r² t'²
- 両辺から r² t'² を移項して整理すると (c² − r²) t'² = 4 a²
- よって t'² = 4 a² / (c² − r²) = (4 a² / c²) · 1/(1 − r²/c²)
- 正の平方根を取って、t' = (2 a / c) · 1/√(1 − r²/c²)
ここで 2a/c は固有時間 t に等しいので、
t' = t / √(1 − r²/c²)
と書けます。右辺の係数 1/√(1 − r²/c²) はローレンツ因子 γ(ガンマ)で表され、γ = 1/√(1 − v²/c²) です。したがって、動いている時計の「1ティックに要する時間」は静止している時計での時間に γ を掛けたものになり、動いている時計は遅れて見える(時間が拡張される)ことが示されます。
物理的解釈と補足
- 正確な意味:t は光時計自身が測る「固有時間(時計に貼りついた観測者が測る時間)」、t' は地上の観測者が観測するその同じティックの時間です。t' ≥ t であり、速度 r が大きくなるほど差は大きくなります。
- 低速極限:r ≪ c のとき、√(1 − r²/c²) ≈ 1 − ½(r²/c²) なので時間の差は非常に小さく、ニュートン力学で問題にならない範囲です。
- 実験的証拠:ミュー粒子の寿命延長や、原子時計を載せた航空機の実験、GPS衛星の時刻補正など、時間拡張は実際に観測・利用されています。
数値例
例えば、もし光時計の固有周期が t = 1.0 秒で、宇宙船が r = 0.5 c(光速の半分)で移動しているとすると、ローレンツ因子は
γ = 1 / √(1 − 0.5²) = 1 / √0.75 ≈ 1.1547
よって地上の観測者が見る1ティックの時間は t' = γ t ≈ 1.1547 秒となり、船内の時計は地上から見ると約15.5%遅れているように見えます。
まとめ
光時計の簡単な幾何学的解析から、特殊相対性理論における時間拡張(moving clocks run slow)の式が導けます。鍵となるのは「光速一定」の原理とピタゴラスの定理を用いた経路長の計算であり、結果として観測される時間はローレンツ因子 γ で拡大されることが示されます。
さらに詳しい数値実験や可視化は次のページで試せます:
http://www.1728.org/reltivty.htm
質問と回答
Q:ライトベルとは何ですか?
A:光時計は、特殊相対性理論の基本的な性質を実証するために作られた装置です。遠くの鏡にフラッシュを反射させ、その反射光で次のフラッシュを発生させ、その間に何回フラッシュが発生したかをカウントする仕組みになっています。
Q:時間拡張とは何ですか?
A:宇宙船が飛ぶのを地球上の人が光時計で見たときに起こる現象が「時間差」です。相対性理論の影響を受けて、比較的ゆっくりと時を刻んでいるように見えるのだ。
Q:宇宙船の中でどれだけ時間が遅くなるかを計算するにはどうしたらいいのでしょうか?
A:代数学とピタゴラスの定理を使って、宇宙船の中でどれだけ時間が遅くなるかを計算することができます。d = rt(距離は速さに時間をかけたものに等しい)という方程式を適用し、光速cを一定にすることを2つの問題で使う必要があるのです。
Q:光時計の仕組みは?
A: 光時計は、上部に鏡がある長い棒の下部に光源があり、下部に電子検出器がある構造です。スイッチを入れると、下から上へ一条の閃光が通り、下部の検出器で検出されると下方に反射し、付属のカウンターに1つ加算され、再び上方へ閃光を発する。この処理は、停止またはリセットされるまで継続されます。
Q:この計算にはどんな方程式が必要ですか?
A: t' = 2a/(c√(1-r2/c2)) が必要で、ここで t' (北極の時計の刻む間隔) は 2a/c を √(1-r2/c2) で割ったものに相当します。t = 1秒、光速の半分の速度で移動する場合、t' = 1.1547秒となります。
Q. この計算とピタゴラスの定理はどのように関係しているのでしょうか?
A:ピタゴラスの定理でh(斜辺)を求めますが、このhは1刻みが何秒続くかを計算する式(d=ct)の一部となります。hがわかれば、t'が求まり、北極から見ている地球上の人々と、その上を高速で通過している船内の人々によると、それぞれの縫い目がどのくらい続くかがわかるのである。
百科事典を検索する