右手の法則（定義と手順）—ベクトルのクロス積で方向を示す方法
右手の法則は、ベクトルの数学でよく使われる慣例で、二つのベクトルのクロス積（外積）で生じる方向を覚えるための方法です。クロス積の結果は両方のベクトルに対して垂直な方向を持ち、その向きは右手の向きに対応します。
手順
- まず右手を自然に開き、親指・人差し指・中指が互いに直角になるようにします。
- 次に、銃のサインのように形を作るか、または親指・人差し指・中指をそれぞれ直角に伸ばします。このとき、親指を第一ベクトル（A）の方向に向け、人差し指を第二ベクトル（B）の方向に向けると、中指が A × B（AとBのクロス積）の方向を示します。
- 向きを確かめるコツとしては、手首を回しても構いません。重要なのは親指→人差し指→中指が右手系の向き（互いに直交し、親指→人差し指の回転が中指の向きと一致する向き）になっていることです。
性質と具体例
- 向き：クロス積 A × B は A と B の両方に垂直な方向を持ち、右手の法則で決まります。
- 大きさ：|A × B| = |A||B| sin θ（θ は A と B のなす角）で、二つのベクトルが平行または反平行なら 0 になります。
- 反可換性：順序を入れ替えると符号が反転します。つまり A × B = −(B × A) です。
- 座標軸の例：標準的な直交座標系では i × j = k、j × k = i、k × i = j となり、逆順では符号が逆になります（j × i = −k など）。
- 物理での利用例：力のモーメント（トルク）τ = r × F、磁場中の荷電粒子に働く力 F = q v × B など、方向が重要な場面で使われます。
実際に二つのベクトルの順序を間違えると向きが逆になります。したがって、親指（第一ベクトル）×人差し指（第二ベクトル）＝中指（積の方向）という順序を常に意識してください。
ねじ山で生成される運動の右手の法則
左が左利きの向き、右が右利きの向きを示しています。
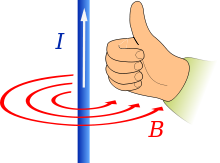
親指の方向に電流Ｉが流れた場合の場の方向予測（Ｂ）について
バリエーション
他にも、磁場や回転するものに使われる「右握りルール（またはコルク抜きルール）」と呼ばれるルールがあります。
1. 右手を平らにして、他の指と直角になるように親指をまっすぐに出すことから始めます。
2. 今、拳にあなたの指をカールし、あなたの親指を（サムズアップのように）外に保つ。
3. 指の巻き方を、何かの動きに合わせます。親指が指している方向は、私たちが話をするときに使うベクトルの方向です。
親指をベクトルの方向に向けてスタートさせ、指がどのように丸まっているかを見て回転方向を見ることで、逆のことができます。親指を針金の電流の方向に向けると、針金の周りに上がってくる磁場は、指が丸まっている方向になります。
質問と回答
Q:右手の法則とは何ですか?
A: 右手の法則とは、ベクトル数学の慣例で、ベクトルが掛け合わされたときに方向を覚えるのに役立ちます。
Q: 右手の法則を使用して、どのようにクロスプロダクトの方向を把握するのですか?
A: クロスプロダクトの方向を知るには、右手を閉じて、ポインターフィンガーを出します。親指は、銃のサインを作るようにまっすぐ上に突き出す。銃」をまっすぐ前に向け、中指を左に向け、すべての指が直角になるように突き出す。親指を1つ目のベクトルの方向に向け、ポインターを2つ目のベクトルの方向に向けます。中指はクロスプロダクトの方向を指すことになる。
Q: ベクトルが掛け合わされるときに順番を変えるとどうなるのでしょうか?
A: ベクトルを掛け合わせる際に順番を変えると、結果が逆になってしまいます。従って、親指×ポインタ＝真ん中の順番になるようにすることが重要です。
Q: この式は何を意味するのか?{Displaystyle {vec {thumb}}times {vec {pointer}}={vec {middle}} .
A: この式は、2つのベクトルを掛け合わせると（親指×ポインタ）、3番目のベクトル（真ん中）になることを意味します。
