ベクトルとは？初心者向け定義・性質・図解でわかる大きさと方向

A vector

ベクトルとは、大きさ（マグニチュード）と方向を持つ数学的な物体のことです。

例えば、何かが動いたときの距離や方向を示すのがベクトルです。道を尋ねたときに、人が「北に向かって1キロ歩いてください」と言えば、それはベクトルです。方向を示さずに「Walk one kilometer」と言われたら、それはスカラーになります。

ベクトルは通常、矢印で描きます。矢印の長さは、ベクトルの大きさに比例します。また、矢印が指す方向がベクトルの方向です。

基本的な表記と成分表示

ベクトルは太字の文字や上に矢印を付けて表すことが多いです（例：a、vや矢印付きで v→）。座標平面では成分で表します。2次元なら v = (v_x, v_y)、3次元なら v = (v_x, v_y, v_z) のように書きます。

大きさ（長さ）と単位ベクトル

ベクトル v = (v_x, v_y) の大きさ（長さ、ノルム）は次の式で求められます。

|v| = √(v_x² + v_y²)

例：v = (3, 4) のとき |v| = √(3² + 4²) = 5 です。大きさが1のベクトルを単位ベクトルと呼び、方向だけを示したいときに使います。

ベクトルの演算（初心者向け）

ベクトルは次のような基本演算ができます。

加法：同じ次元のベクトルどうしは成分ごとに足せます。例えば a = (a_x, a_y)、b = (b_x, b_y) のとき a + b = (a_x + b_x, a_y + b_y)。図では平行四辺形の法則や端点をつなぐ方法で表現できます。
減法：a − b = a + (−b)。負のベクトル (−b) は向きが逆のベクトルです。
スカラー倍（実数倍）：実数 k とベクトル v に対し k·v = (k v_x, k v_y)。k が負なら向きが反転します。

内積（ドット積）と角度

2つのベクトル a = (a_x, a_y)、b = (b_x, b_y) の内積は

a · b = a_xb_x + a_yb_y

また内積は大きさと角度を使って次のようにも表せます。

a · b = |a| |b| cosθ（θ は a と b のなす角）

この式から、内積が0なら2つのベクトルは直交（垂直）していることがわかります。

外積（クロス積：3次元）

3次元ベクトルに対しては外積（クロス積）を定義できます。a × b は a と b に垂直なベクトルで、その大きさは

|a × b| = |a| |b| sinθ

方向は右ねじの法則（右手の法則）で決まります。外積は面積やトルクの計算に使われます。

重要な性質（まとめ）

ベクトルの和は可換：a + b = b + a。
分配法則：k(a + b) = ka + kb。
内積はスカラーを返し、外積はベクトルを返す（3次元）。
零ベクトル（0）は大きさ0で向きが定義されない特殊なベクトルです。
ベクトルが平行（または反平行）であれば一方はもう一方のスカラー倍で表せます（共線/共平面性）。

図でのイメージ

矢印の始点→終点をイメージしてください。加法は「矢印をつなげる」ことで合成され、スカラー倍は矢印の長さを伸縮させます。内積は矢印の向きが近いほど大きく、外積は二つの矢印で作られる平行四辺形の面積に相当します。

具体例と応用

物理学：速度、加速度、力などはベクトルで表されます（方向と大きさが重要）。
地図・ナビゲーション：方向と距離の指示はベクトル的な情報です。
コンピュータグラフィックス：位置や法線、光の方向などをベクトルで計算します。
データ解析・機械学習：特徴量をベクトルとして扱い、内積やノルムで類似度や大きさを測ります。

学ぶときのポイント

まずは2次元の成分表示と図による直感（矢印の長さと向き）を理解し、その後に内積・外積や応用例に進むと学びやすいです。簡単な計算（例：(3,4) の長さを求める、(1,2) と (3,4) の和を求める）を手でやってみると理解が深まります。

以上がベクトルの基本的な定義、性質、図での考え方と主な応用です。さらに詳しく学びたい場合は、座標変換、基底と次元、線形独立といった線形代数学の概念に進むと理解が広がります。

ベクトルの例

ジョンは北へ20メートル歩きます。北」という方向と「20メートル」という距離を合わせたものがベクトルです。
リンゴが秒速10メートルで下に落ちます。下」という方向と「秒速10メートル」という速度を合わせたものがベクトルです。このようなベクトルは速度とも呼ばれます。

スカラーの例

2つの場所の間の距離は10kmです。この距離は、方向を含んでいないので、ベクトルではありません。
箱に入っている果物の数は、ベクトルではありません。
人が指差すことは、方向だけがあるので、ベクトルではありません。大きさ（例えば、人の指から建物までの距離）もありません。
オブジェクトの長さです。
車は時速100kmで走っています。これは、大きさがあるだけで方向がないため、ベクトルを表すものではありません。

ベクトルのその他の例

変位とはベクトルのことです。変位とは、何かがある方向に移動する距離のことです。距離だけの尺度はスカラーです。
方向性を含んだ力をベクトルといいます。
速度は、ある方向への速さなので、ベクトルです。
加速度とは、速度の変化率のことです。物体が速度を変えたり、方向を変えたりしている場合、その物体は加速していることになります。

ベクトルの付け方

ヘッド・トゥ・テール法による紙面上でのベクトルの付加

Head to Tail法は、2つのベクトルを加算した結果を紙の上で推定するのに便利です。その方法とは

それぞれのベクトルは、後ろに長さのある矢印として描かれており、紙の上の長さの各単位は、ベクトルのある大きさを表しています。
2番目のベクトルのテール（端）が1番目のベクトルのヘッド（前）になるように、次のベクトルを描きます。
これをさらにすべてのベクターについて繰り返します。次のベクトルのテールを前のベクトルのヘッドに描く。
最初のベクトルの末尾から最後のベクトルの先頭まで線を引くと、それがすべてのベクトルの結果（和）になります。

これは、前のベクトルの頭が次のベクトルの尻尾につながることから、「ヘッド・トゥ・テール」方式と呼ばれています。

コンポーネントフォームの使用

^{[d]が説明必要です。}

2つのベクトルの足し算に成分形式を使うと、文字通り、ベクトルの成分を足して新しいベクトルを作ることになります。例えば，aとbを2次元のベクトルとします。これらのベクトルは、その成分で書くことができます。

a = ( a x , a y ) {\\bf {a} =(a_{x},a_{y})}。 $\mathbf {a} =(a_{x},a_{y})$

b = ( b x , b y ) {\\bf {b} =(b_{x},b_{y})}。 $\mathbf {b} =(b_{x},b_{y})$

これにより、c = ( a x + b x , a y + b y ) {displaystyle ˶‾᷄ -̫ ‾᷅˵ {c} =(a_{x}+b_{x},a_{y}+b_{y})} $\mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})$ となる。

ここでは、2つのベクトルの成分形を使った加算の例を紹介します。

a = ( , - ) {\\31bf {a} =(3,-1)}。 $\mathbf {a} =(3,-1)$

b = ( , ) {\\22bf {b} =(2,2)}。 $\mathbf {b} =(2,2)$

c = a + b {\\\\\\\\\\\\\\⁾⁾⁾⁾⁾⁾⁾⁾⁾⁾⁾⁾。} $\mathbf {c} =\mathbf {a} +\mathbf {b}$

= ( a x + b x , a y + b y ) {\displaystyle =(a_{x}+b_{x},a_{y}+b_{y})}。 $=(a_{x}+b_{x},a_{y}+b_{y})$

32= ( + , - + ) { {12displaystyle =(3+2,-1+2)}。 $=(3+2,-1+2)$

= ( , ) { {51displaystyle =(5,1)}。 $=(5,1)$

この方法は、2次元のものだけでなく、すべてのベクトルに対応しています。

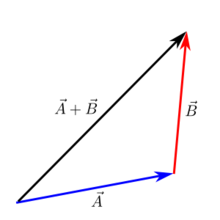
ヘッド・トゥ・テールの追加

ベクトルの掛け算の方法

ドットプロダクトの使用

ベクトルを乗算する方法の一つとして、ドットプロダクトがあります。スカラーを生成します。コンポーネント形式を使用します。

a 2= ( , ) 3b 1= ( , ) 4a ⋅ b = ( , 2)3 ⋅ ( , 1) 4213421214= ( ⋅ ) + ( ⋅ ) = + = {\displaystyle {\begin{aligned}\mathbf {a} =(2,3）\\\\\\\\\\\\\\\\\\\\\\\\\\\\\⁾⁾。 ${\begin{aligned}\mathbf {a} =(2,3)\\\mathbf {b} =(1,4)\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\=(2\cdot 1)+(3\cdot 4)\\=2+12=14\end{aligned}}$

クロスプロダクトの使用

交差積は、ベクトルを乗算するもう一つの方法です。別のベクトルを生成します。成分形を使って

a × b = | a | b | sin ( θ ) n {\displaystyle ˶‾᷄ -̫ ‾᷅˵} =||mathbf {a} =||mathbf {b} =||mathbf {a} =||mathbf| |mathbf {b}}|sin(in theta )・\\mathbf {n}。} $\mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n}$

ここで、a｜{\\mathbf {a}}は、長さを意味する。|の長さを $|\mathbf {a} |$ 意味する。の長さを意味し $\mathbf {a}$ ，nは{\\}の長さを意味する．はaとbに直角な単位ベクトルで $\mathbf {n}$ ある。 $\mathbf {a}$ とbに直角な単位ベクトルである。} $\mathbf {b}$ .

スカラーの乗算

ベクトルとスカラー（通常の数値）を掛け合わせるには、ベクトルの各成分に数値を掛け合わせます。

c x = ( c x ,1 c x , ... ,2 c x n ) {˶‾᷄ -̫ ‾᷅˵} {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})}。 $c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})$

その一例として

c = x 53= ( , )4 c x 55= ( ⋅ , ⋅ ) = ( , ) {\\{341520begin{aligned}c=5\\\\{x} =(3,4)୨୧{x} =(5cdot 3,5\cdot 4)୨୧{end{aligned}}}。 ${\begin{aligned}c=5\\\mathbf {x} =(3,4)\\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\=(15,20)\end{aligned}}$

質問と回答

Q:ベクトルとは何ですか?

A:ベクトルとは、大きさ（マグニチュード）と方向（ディレクション）を持つ数学的なオブジェクトです。太字で表現されたり、ある点から別の点への線分として表現されることが多いです。

Q:通常、ベクトルはどのように描かれるのですか?

A:私たちは通常、ベクトルを矢印で描きます。矢印の長さはベクトルの大きさに比例し、矢印が指す方向がベクトルの方向となります。

Q:道を聞かれるとはどういうことですか?

A:道を尋ねるとき、「北に向かって1キロ歩いてください」と言えばベクトルになりますが、方向を示さずに「1キロ歩いてください」と言えばスカラーになります。

Q:ベクトルはどのように使われるのですか?

A:ベクトルは、何かが動いた距離と方向を示すために使うことができます。また、道を尋ねるときや、ある場所を移動するときにも使うことができます。

Q:数学的にベクトルはどのように表現されますか?

A:ベクトルは、太字（u、v、wなど）や、ある点から別の点への線分（A→Bのように）で表現されることが多いです。

Q:スカラーとはどういう意味ですか?

A:スカラーと呼ばれるものは、方向性を持たず、距離や速度などの数値のみで表現されることを意味します。