ヤング・ラプラスの式
物理学では、ヤングラプラス方程式(/ləˈplɑːs/)は、水と空気などの2つの静的流体の界面を横切る毛細管圧差を記述する非線形偏微分方程式である。この差は、表面張力または壁張力という現象によるものです。壁張力は、非常に薄い壁にしか使用できません。ヤング・ラプラス方程式は、圧力差を表面または壁の形状に関連づけます。静的な毛細管表面の研究では非常に重要です。
生理学ではラプラスの法則として知られています。中空の臓器内の圧力を説明するために使用されます。
この方程式は、1805年に表面張力の質的理論を開発したトーマス・ヤングと、翌年に数学的記述を完成させたピエール＝シモン・ラプラスにちなんで名付けられました。また、ヤング-ラプラス-ガウス方程式と呼ばれています。カールフリードリヒガウスは、1830年にヤングとラプラスの仕事を統一した。ガウスは、微分方程式と境界条件の両方をヨハンベルヌーイの仮想作業原理を使用して導出した。
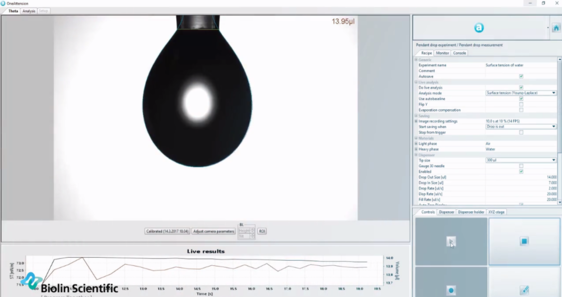
光学式テンシオメーターは、ヤングラプラス式を用いて、ペンダント液滴の形状から液面張力を自動判定します。
質問と回答
Q:ヤング・ラプラス方程式とは何ですか?
A: ヤング・ラプラス方程式は、水と空気など2つの静止流体の界面における毛管圧差を記述する非線形偏微分方程式である。
Q: 何が関係しているのですか?
A: 圧力差と表面や壁の形状を関係づけています。
Q: この理論は誰が開発したのですか?
A: 1805年にトーマス・ヤングによって開発され、翌年にはピエール＝シモン・ラプラスによって数学的に記述されました。その後、1830年にカール・フリードリヒ・ガウスによって統一されました。
Q:生理学ではどのように使われているのですか?
A: 生理学では、ラプラスの法則と呼ばれ、中空臓器内の圧力を説明するために使用されます。
Q: どのような現象を説明するのですか?
A: ヤング・ラプラスの式は、表面張力や壁張力という現象を説明します。
Q: 壁張力は厚い壁にも適用できるのですか?A:いいえ、壁張力は非常に薄い壁に対してのみ使用できます。
