表面張力とは|定義・原理・日常例と材料科学での応用
表面張力の定義・原理を図解でわかりやすく解説。日常例から表面エネルギー・材料科学での応用まで実例で学べる入門ガイド。
表面張力とは、液体の表面が収縮して平らになろうとする性質で、表面を「薄い膜」のように強く振る舞わせる現象です。表面付近の分子は内部の分子と比べて周囲の結合相手が少ないため、より高いエネルギー状態にあり、その結果として表面積を減らそうとする力が働きます。この力により水滴は球状になり、小さな物体でも本来は沈まないような場合に水面に浮くことがあります。たとえば、昆虫(アメンボなど)は足の上の水をはじく性質と表面張力を利用して水面を歩くことができます。表面張力は、液体中の分子同士が引き合う凝集性によって生じ、液体の挙動の多くを支配しています。
定義と原理
表面張力には次の2つの見方があります。ひとつは「単位長さあたりの力」(N/m)としての表面張力、もうひとつは「単位面積あたりのエネルギー」(J/m²)としての表面エネルギーです。これらは数値的に等価であり、液体表面に新しい面積を作るために必要な仕事として理解できます。なお、単位面積当たりのエネルギーという観点からは、液体だけでなく固体にも適用されるため、より一般的な用語として表面エネルギーという言葉が使われます.
単位と代表的な式
表面張力は通常ギリシャ文字のγ(ガンマ)で表され、単位はN/m(ニュートン毎メートル)またはJ/m²(ジュール毎平方メートル)です。曲面を持つ液滴内部の圧力差はヤング–ラプラスの式で表されます:ΔP = γ(1/R1 + 1/R2)、ここでR1、R2は主曲率半径です。また、固体に液滴が接するときの濡れ性は接触角θで記述され、ヤングの式 γ_SV − γ_SL = γ_LV cosθ(γ_SV:固体-蒸気表面エネルギー、γ_SL:固体-液体界面エネルギー、γ_LV:液体-蒸気表面張力)で関係づけられます。
身近な例と現象
- 水滴が丸くなる:表面張力は表面積を最小にする形(球)を作る力です。
- アメンボや水に浮く針:表面張力が働くことで物体が沈まず表面に乗ることができる。
- 毛細管現象:細い管内で液体が上昇(または下降)するのは表面張力と接触角による力のつり合いから生じます。
- 石鹸や洗剤の効果:界面活性剤(サーファクタント)は表面張力を低下させ、汚れや油を水に混ざりやすくします。
- マランゴニ(Marangoni)効果:表面張力の空間差により液体内部で流れが生じる現象。温度差や濃度差で起こります。
測定方法
表面張力や表面エネルギーの測定にはいくつかの代表的な手法があります。代表的なものに、デュ・ヌイ(du Noüy)リング法、ウィルヘルミー(Wilhelmy)プレート法、毛細管上昇法、滴下法(滴の形状からγを導く方法)などがあります。実験条件(温度、清浄度、気体の種類)によって値が変わるため、適切な前処理と校正が重要です。
影響因子
表面張力は以下の因子で変化します:
- 温度:一般に温度が上がると表面張力は低下します。
- 不純物や界面活性剤:表面に吸着する物質は表面張力を大きく変える(通常は低下)ことがあります。
- 溶質の種類と濃度:電解質や有機溶媒の混合比などによっても影響されます。
材料科学での応用
材料科学の分野では、表面張力(より一般には表面エネルギー)は表面処理、薄膜形成、接着、濡れ性制御、自己組織化やナノ粒子の安定化など多岐にわたって重要です。表面エネルギーを制御することで塗料や接着剤の広がり方を調整したり、マイクロ流体デバイスで液体の移動を制御したり、薄膜の成長モードを決めることができます。また、固体の表面応力と表面自由エネルギー(表面張力に対応する概念)は、微小構造の変形や応力発生にも関係します。設計上は、表面処理で親水化・疎水化を行ったり、界面活性剤を用いて薄膜の均一化を図るなどの応用が典型的です。
まとめ
表面張力は、分子間の凝集力に由来する液体表面の性質で、エネルギーや力として定量化されます。日常の現象(滴の形、昆虫の水上移動、洗剤の働き)から高機能材料の設計(濡れ性制御、薄膜形成、ナノ材料の安定化)まで、幅広く関係する基本的かつ実用的な物理量です。
コーズ
液体の分子間の凝集力が表面張力の原因となる。液体の大部分では、各分子は隣り合う液体分子によってあらゆる方向に均等に引っ張られ、正味の力はゼロとなる。表面の分子は、四方に他の分子がないため、内側に引っ張られる。これにより、ある程度の内圧が発生し、液体の表面は最小限の面積まで収縮することになる。
液滴の形は表面張力によって決まる。水滴は変形しやすいが、表面層の凝集力によって球形に引き寄せられる傾向がある。重力などの他の力がなければ、ほとんどすべての液体の液滴は完全な球形になる。球状になることで、ラプラスの法則に基づく表面層の「壁の張力」が最小限に抑えられる。
別の見方をすれば、エネルギーの観点から見ることができます。隣人と接触している分子は、単独の場合(隣人と接触していない場合)よりもエネルギーが低い状態にあります。内部の分子は隣人をできるだけ多く持っていますが、境界分子は(内部の分子に比べて)隣人がいない状態です。つまり、境界分子の方がエネルギーが高いのです。液体のエネルギー状態を最小にするためには、エネルギーの高い境界分子の数を最小にしなければなりません。境界分子の数が最小になると、表面積が最小になります。
表面積を最小にするために、表面はできる限り滑らかな形状になります。表面の形状が湾曲していると、面積が大きくなり、エネルギーも大きくなります。そのため、坂道を上っていくボールが、重力による位置エネルギーを最小にするために押し戻されるのと同じように、表面は曲率に対して押し戻されます。
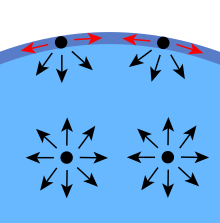
液体中の分子に働く力の図

表面張力により、ペーパークリップが沈まない。
日常生活における効果
水
水を調べると、表面張力の影響がいくつか見られます。
A.雨水は、葉っぱなどのワックス状の表面に数珠状になって付着します。水はワックスには弱く、自分自身には強く付着するので、水滴として集まります。球体は表面積と体積の比率が最も小さいため、表面張力によって球形に近い形になる。
B.液滴の形成は、液体の塊が引き伸ばされたときに起こります。このアニメーションでは、蛇口に付着した水が質量を増し、表面張力によって蛇口に縛り付けられなくなるところまで引き伸ばされます。そして、水滴は分離し、表面張力によって球状になります。もし蛇口から水が流れていたら、その流れは落下中に水滴に分解されます。重力が水流を伸ばし、表面張力が水流を球状にします。
C.水よりも密度の高い物体でも、物体が濡れておらず、その重量が表面張力によって負担できるほど小さい場合には浮く。例えば、アメンボは表面張力を利用して池の水面を歩きます。水面は弾性のあるフィルムのようなもので、虫の足が水面にくぼみを作り、表面積を増やしているのだ。
D.油と水(ここでは水と液体ワックス)の分離は、異種の液体間の表面の張力によって起こります。この種の表面張力は「界面張力」と呼ばれていますが、その物理的性質は同じです。
E.ワインの涙」とは、アルコール飲料の入ったグラスの側面に、水滴や小水ができることである。その原因は、水とエタノールの表面張力の違いによる複雑な相互作用である。エタノールによって水の表面張力が変化することと、エタノールが水よりも速く蒸発することが重なって生じる。
· 
A.葉っぱの上の水のビーディング
· 
B.蛇口から滴る水
· 
C.アメンボは表面張力によって液体の上に留まる
· 
D.水と液体ワックスという異種の液体の相互作用を利用した溶岩ランプ
· 
E.ワインの涙 "現象を示す写真。
界面活性剤
表面張力は他の一般的な現象でも目にすることができ、特に界面活性剤を使用して表面張力を低下させる場合には、その効果が顕著に現れます。
- シャボン玉は表面積が非常に大きく、質量はほとんどありません。純水の中のシャボン玉は不安定です。しかし、界面活性剤を添加すると、シャボン玉を安定させる効果があります(マランゴニ効果参照)。なお、界面活性剤は水の表面張力を3倍以上に低下させます。
- エマルションとは、表面張力が関与する溶液の一種である。純水に浮かんだオイルの小さな断片は、自然に集まって大きな塊になる。しかし、界面活性剤が存在すると表面張力が低下し、水の中にある微小な油滴を安定させることができる(またはその逆)。
基礎物理学
2つの定義
表面張力はγという記号で表され、単位長さの線に沿って、表面に平行で線に垂直な方向に働く力と定義される。これをイメージするには、平らな石けん膜の片側に長さLの糸が張ってある状態を想像すればよい。糸はγ2に等しい力で膜の内側に向かって引っ張られる。
これに相当する定義として、熱力学では「単位面積当たりの仕事量」が挙げられる。そのため、ある質量の液体の表面積をδAという量だけ増加させるためには、γ{\\gamma}という量の仕事が必要になります。
単位面積当たりのエネルギーと単位長さ当たりの力の測定の同等性は、寸法分析によって証明することができます。
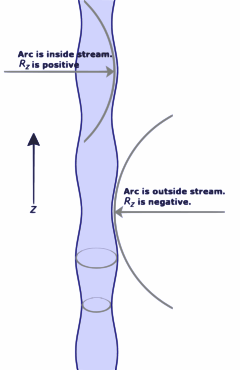
表面の曲率と圧力
張られた表面の法線方向に力が働かなければ、表面は平らなままでなければなりません。しかし、表面の一方の側の圧力と他方の側の圧力が異なる場合、圧力差に表面積を乗じたものが法線方向の力となります。表面張力の力が圧力による力を打ち消すためには、表面を曲げる必要があります。図は、小さな表面のパッチが曲がっていると、パッチの中心に対して垂直方向に働く表面張力の正味の成分が生じる様子を示しています。すべての力が相殺されると、ヤング・ラプラス方程式と呼ばれる式が得られます。
Δ p = γ ( R 1x + R1 y ) {\\\\\\\\\\\\\\\\\⁾⁾。
のところです。
· Δpは圧力差。
· γ{displaystyle ″scriptstyle ″gamma ″}は表面張力で
· RxとRyは曲面に平行な各軸の曲率半径。
右辺の( )内の量は、実際には(正規化によって)表面の平均曲率の(2倍)です。
この方程式の解によって、水滴、水たまり、メニシキ、シャボン玉など、表面張力で決まるすべての形状が決まります。(また、アメンボの足が池の表面に作る印象の形なども、この方程式に基づいて決定されます。)
下の表は、水滴の半径が小さくなるにつれて、水滴の内圧が大きくなることを示しています。小さくない水滴ではその効果はわずかですが、水滴の大きさが分子の大きさに近づくと、圧力差が大きくなります。(分子1個の限界では、この概念は意味をなさない)
| STPにおける様々な半径の水滴のΔp | ||||
| 液滴の半径 | 1mm | 0.1mm | 1μm | 10nm |
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
液面
任意の形をした枠に囲まれた極小面の形を、数学だけで見つけるのは難しい。しかし、針金で作った枠を石けん液に浸すと、数秒で石けん膜の中に局所的な最小面が現れる。
その理由は、ヤング・ラプラス方程式に見られるように、流体界面の圧力差は平均曲率に比例するからである。開放された石鹸膜の場合、圧力差はゼロであるため、平均曲率はゼロとなり、極小表面は平均曲率ゼロの特性を持つことになる。
接触角
液体の表面は、その液体と他の媒体との境界である。例えば、池の上面は、池の水と空気との界面です。つまり、表面張力は、液体単体の性質ではなく、液体と他の媒体との界面の性質なのです。液体が容器に入っている場合、その上面の液体と空気の界面のほかに、液体と容器の壁の界面があります。液体と空気の間の表面張力は、通常、容器の壁との間の表面張力とは異なる(大きい)。2つの表面が出会うところでは、幾何学的にすべての力が均衡します。
2つの表面が出会うところでは、接触角θが形成される。


γ l a > γ l s - γ s a > {\\\\\\\\\\\\\\\\0⁾⁾。♪♪♪♪♪♪♪~♪♪~}\ >\ 0}
この図では、垂直方向の力と水平方向の力の両方が接触点で正確に相殺されなければならず、これを平衡状態といいます。水平方向の力であるf l aは、接着力であるf Aによって打ち消される。の水平方向の成分

f A = f l a sin θ {displaystyle f_{\mathrm {A}}}\♪♪♪♪♪~sin ♪♪♪♪♪♪♪}
しかし、より重要な力のバランスは、垂直方向にある。f l a の垂直成分は、f l s の力を正確にキャンセルしなければならない。の垂直成分は、f l s {\\\}の力を正確にキャンセルし

f l s - f s a = - f l a cos θ {displaystyle f_{\mathrm {ls}}-f_{\mathrm {sa}}。}-f_{\\{sa}.Ms.cos Θ}
| 液体 | ソリッド | 接触角 | |||
| 0° | ||||
| ジエチルエーテル | |||||
| 四塩化炭素 | |||||
| グリセロール | |||||
| 酢酸 | |||||
| パラフィンワックス | 107° | ||||
| 銀 | 90° | ||||
| ヨウ化メチル | ソーダライムグラス | 29° | |||
| 鉛ガラス | 30° | ||||
| フューズドクオーツ | 33° | ||||
| ソーダライムグラス | 140° | ||||
| いくつかの液体-固体接触角 | |||||
この力は、それぞれの表面張力に比例するので、次のようにもなります。
γ l s - γ s a = - γ l a cos θ {˶ˆ꒳ˆ˵ )-gamma _{\mathrm {sa}}-gamma _{\mathrm {sa}}。♪♪♪♪♪♪♪~cos\\\\}
どこで
· γ l s {\displaystyle \scriptstyle \gamma _{\mathrm {ls}}}
· γ l a {displaystyle scriptstyle ˶‾᷄ -̫ ‾᷅˵ }}は液体-空気間の表面張力である。}}
· γ s a {\\\\\\\\ }}は固体空気の表面張力である。}}は固体空気表面張力
· θ {displaystyle ″scriptstyle ″theta″
これは、液体-固体間と固体-空気間の表面張力の差、γ l s - γ s a があるものの}-gamma _{\\{sa}}。}}


これと同じ関係が右の図にもあります。しかし、この場合、接触角が90°以下であるため、液体-固体-空気の表面張力差は負でなければならないことがわかります。
γ l a 0> > γ l s - γ s a {\\\\\\\\\\\\\\\\\\\\\\\\\\\\⁾⁾。0%\\\\です。♪♪~}}
特殊な接触角
水と銀の界面で接触角が90°という特殊なケースでは、液体と固体、空気と固体の表面張力の差が正確にゼロになることに注目してください。
もう一つの特殊なケースは、接触角がちょうど180°になる場合です。特別に用意されたテフロンを使った水がこれに近づく。接触角が180°になるのは、液体-固体間の表面張力と液体-空気間の表面張力がちょうど一致する場合です。
γ l a = γ l s - γ s a >0 θ 180= ∘ {displaystyle ˶‾᷄ -̫ ‾᷅˵ }\\♪♪♪♪♪~♪♪~0\\\\\\\\\\\\\\\\\\\\\\\
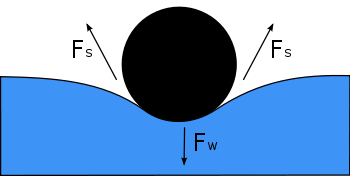
図は、水面に浮かぶ針を断面で表したもの。針の重さFwは水面を押し下げ、針と接する位置で水面に平行に働く左右の表面張力Fsと釣り合っています。2本のFsの矢印の水平成分は反対方向を向いているので打ち消し合うが、垂直成分は同じ方向を向いているので、足し合わせるとFwが釣り合うことに気づく。
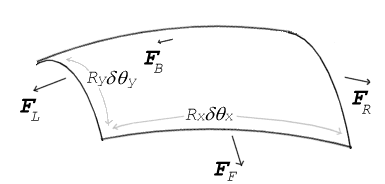
小さな(差分)パッチの表面に働く表面張力の力。δθx、δθはパッチの寸法以上の曲げ量をy示す。引張力と圧力のバランスをとると、ヤングラプラス方程式が導かれる

最小限の表面
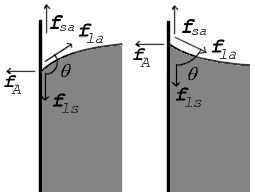
接触角が90°より大きい場合(左)と90°より小さい場合(右)の接触点における力を示す。
測定方法
表面張力にはさまざまな効果があるため、その測定方法もさまざまです。どの方法が最適かは、測定する液体の性質、張力を測定する条件、変形したときの表面の安定性などによって異なります。
- Du Noüy Ring法。表面張力や界面張力の測定に用いられる伝統的な方法。表面や界面の湿潤性はこの測定法にほとんど影響しない。表面からリングにかかる最大の力を測定する。
- デュ・ヌーイ-パドデイ法。Du Noüy法を最小化したもので,リングの代わりに小径の金属針を用い,高感度マイクロバランスと組み合わせて最大吸引力を記録する。この方法の利点は,非常に少量の試料(数十マイクロリットルまで)を,浮力を補正することなく(適切な形状の針または棒の場合),非常に高い精度で測定できることです。さらに、測定は非常に迅速に行うことができ、最短で約20秒で完了します。この原理に基づいて、初の商用マルチチャンネル・テンシオメーター[CMCeeker]が最近作られた。
- ウィルヘルミー・プレート法。普遍的な方法で,特に長時間にわたる表面張力の測定に適している。周囲が既知の垂直な板を天秤に取り付け、濡れたときの力を測定する。
- スピニングドロップ法。この手法は、低い界面張力の測定に最適です。重相内の液滴の直径を、両者を回転させながら測定する。
- ペンダントドロップ法。高温高圧下でも、表面張力や界面張力を測定できる手法。液滴の形状を光学的に解析します。詳しくはドロップをご覧ください。
- 気泡圧法(イェーガー法)。短い表面年齢で表面張力を測定するための測定手法。各バブルの最大圧力を測定する。
- ドロップボリューム法。界面張力を界面年齢の関数として測定する方法。ある密度の液体を、異なる密度の第二の液体に注入し、滴ができるまでの時間を測定する。
- キャピラリーライズ法。毛細管の先端を溶液に浸します。溶液が毛細管内に到達する高さは、下記の式で表面張力と関係します。
- スタラグム測定法。液体の一滴を重くして読み取る方法。
- 滴下法。基板上に液滴を置き、接触角を測定することで表面張力や密度を測定する方法(Sessile drop technique参照)。
- 浮遊する滴の振動数超流動4Heの表面張力は、磁力で空中に浮かせた液滴の振動の固有振動数を調べることで測定されている。この値は、T=0°Kで0.375dyn/cmと推定される。

表面張力は、ゴニオメーターを用いたペンダントドロップ法で測定できます。
エフェクト
垂直管内の液体
旧式の水銀気圧計は、直径1cmほどの縦長のガラス管の一部に水銀を充填し、充填されていない部分を真空(トリチェリの真空と呼ばれる)にしたものです(右図参照)。管の中央部の水銀レベルが端部よりも高く、水銀の上面がドーム状になっていることに注目してください。水銀の上面が管の断面全体に渡って平らであれば、水銀柱全体の質量中心はわずかに低くなります。しかし、水銀の上面がドーム状になっていると、水銀の全質量に対する表面積がわずかに小さくなります。この場合も、2つの効果が組み合わさって、全体の位置エネルギーが最小になります。このような表面形状を凸型メニスカスといいます。
水銀はガラスに全く付着しないので、ガラスと接触している部分を含めた水銀の質量全体の表面積を考えます。つまり、水銀の表面張力は、ガラスと接している部分を含めた表面積全体に作用するのです。もし、ガラスではなく、銅でできたチューブだったら、状況は大きく変わります。水銀は銅に積極的に付着します。そのため、銅管では、中央部の水銀のレベルが端部よりも低くなります(つまり、凹状のメニスカスになります)。液体が容器の壁に付着している状況では、液体の表面積のうち、容器と接触している部分は負の表面張力を持っていると考えます。すると、液体は接触面積を最大にしようと働きます。つまり、この場合、容器との接触面積を増やすと、位置エネルギーが増加するのではなく、減少します。この減少は、容器の壁の近くで流体を持ち上げることに伴う位置エネルギーの増加を補うのに十分です。
チューブの幅が十分に狭く、その壁への液体の付着が十分に強い場合、表面張力によって毛細管現象と呼ばれる現象でチューブ内に液体を引き上げることができる。このとき、カラムが持ち上がる高さは次のようになります。
h = γ 2l a cos θ ρ g r {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\⁾⁾。{cos eldest }{\\ gr}}。
どこで
· hは、液体を持ち上げる高さ
· γ l a {displaystyle scriptstyle ˶‾᷄ -̫ ‾᷅˵ }}は液体-空気間の表面張力である。}}
· ρは、液体の密度
· r
· gは、重力による加速度
· θは上述の接触角で

路面上の水たまり
水平に置かれた平板ガラスに水銀を注ぐと、厚さが感じられる水たまりができます。この水たまりは、0.5cm弱の厚さになるところまでしか広がらず、それ以上は広がらない。これもまた、水銀の強い表面張力の働きによるものです。液体の塊が平らになるのは、水銀の量をできるだけ少なくするためですが、同時に表面張力が作用して総表面積を小さくしています。その結果、ほぼ一定の厚さの水たまりという妥協点が生まれるのです。
水でも石灰水でも、あるいは生理食塩水でも、同じように表面張力のデモンストレーションを行うことができますが、それは液体が平らな表面素材に付着していない場合に限られます。ワックスはそのような物質です。滑らかで平らで水平なワックスの表面、例えばワックスを塗ったガラス板に注がれた水は、ガラスに注がれた水銀と同じような挙動を示します。
接触角が180°の表面上の液体の水たまりの厚さは次式で与えられる。
h = γ2 gρ {displaystyle h\\ = 2{˶ˆ꒳ˆ˵} 2{sqrt {˶ˆ꒳ˆ˵} {g\rho }}}}
どこで
| hは、水たまりの深さをセンチメートルまたはメートルで表したもの |
| γ{displaystyle ″scriptstyle ″gamma ″} |
| gは、重力加速度 |
| ρは、液体の密度(グラム/立方センチメートル、キログラム/立方メートル) |
実際には、どの液体に対しても180°の接触角を持つ表面はほとんどないため、水たまりの厚さは上の式で予測される値よりもわずかに小さくなります。接触角が180°未満の場合、厚さは次式で与えられます。
h = γ2 l a 1( - cos θ ) g ρ .{h=γ l ( - cos θ ) gρ.left(1-cos Θ\\ right)}{g\rho }}。}
ガラス上の水銀では、γHg=487dyn/cm、ρHg=13.5g3/cm、θ=140°で、hHg=0.36cmとなる。また、25℃のパラフィン上の水の場合、γ=72dyn/cm、ρ=1.0g3/cm、θ=107°で、hH2O=0.44cmとなります。
また、この式では、接触角が0°のとき、液体は表面上に微小な薄い層を形成して広がると予測しています。このような表面は、液体によって完全に濡れていると言われています。
流れを水滴に分解する
日常生活の中で、蛇口から出る水流がどんなにスムーズであっても、水滴に分解されてしまうことがあります。これは、表面張力の影響による「プラトー・レイリー不安定性」と呼ばれる現象によるものである。
この不安定性を説明するには、まず、流れの中に微小な摂動が存在することから始まる。これは、どんなに滑らかな流れであっても必ず存在します。摂動を正弦波の成分に分解すると、時間とともに成長する成分と、時間とともに減衰する成分があることがわかります。時間とともに成長する成分の中には、他の成分よりも成長速度が速いものがあります。ある成分が減衰するか成長するか、そしてその成長の速さは、波数(1cmあたりの山と谷の数)と、元の円筒形の流れの半径の関数で決まります。
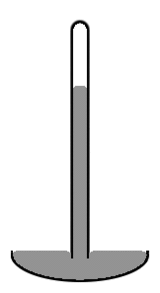
水銀気圧計の図
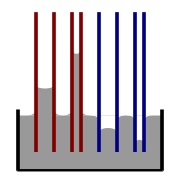
毛細血管の上昇と下降のイラスト。赤=接触角が90°未満、青=接触角が90°以上
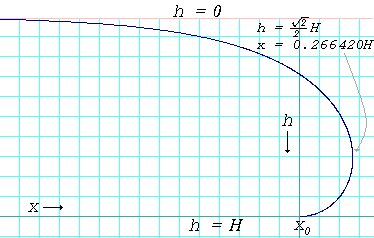
接触角が180°の場合の水たまりの縁のプロファイル曲線。曲線は次の式で与えられる。x-x =0 H12 cosh 1- ( H h ) - H 1- h H2H{sqrt {1-{\\{h^{2}}{H^{2}}}}}} 

滑らかで清潔な表面上の小さな水たまりは、その厚さが感じられます。
接触角が小さいと水たまりの深さが浅くなることを示す図
データテーブル
| 空気に対する各種液体の表面張力(単位:dyn/cm) | ||
| 液体 | 温度 ℃ | 表面張力、γ |
| 酢酸 | 20 | 27.6 |
| 酢酸(40.1%)+水 | 30 | 40.68 |
| 酢酸(10.0%)+水 | 30 | 54.56 |
| アセトン | 20 | 23.7 |
| ジエチルエーテル | 20 | 17.0 |
| エタノール | 20 | 22.27 |
| エタノール(40%)+水 | 25 | 29.63 |
| エタノール(11.1%)+水 | 25 | 46.03 |
| グリセロール | 20 | 63 |
| n-ヘキサン | 20 | 18.4 |
| 塩酸17.7M水溶液 | 20 | 65.95 |
| イソプロパノール | 20 | 21.7 |
| 液体窒素 | -196 | 8.85 |
| 15 | 487 | |
| メタノール | 20 | 22.6 |
| n-オクタン | 20 | 21.8 |
| 塩化ナトリウム6.0M水溶液 | 20 | 82.55 |
| スクロース(55%)+水 | 20 | 76.45 |
| 水 | 0 | 75.64 |
| 水 | 25 | 71.97 |
| 水 | 50 | 67.91 |
| 水 | 100 | 58.85 |
効果のギャラリー
· 
スプーンで跳ね返された動く水のシートのブレイクアップ。
· 
手に付着した水の流れの写真。表面張力により、流れと手の間に水のシートができる。
· 
シャボン玉は、表面張力と内部の空気圧のバランスをとっている。
· 
表面張力はコインが沈むのを防ぎます。コインは水よりも明らかに密度が高いので、浮力が質量と釣り合うためには、自分の体積よりも大きな体積を移動させなければなりません。
· 
ヒナギクのこと。花の全体は、(邪魔されていない)自由表面のレベルより下にあります。水はその縁を滑らかに上昇します。表面張力により、水が花びらの間の空気を満たし、花が水没する可能性がない。
· 
金属製のペーパークリップは水に浮きます。通常、水があふれないように慎重に数個を追加することができます。
· .jpg)
アルミニウムのコインは、10℃の水の表面に浮かんでいます。余分な重さがかかると、コインは底に落ちてしまいます。
質問と回答
Q:表面張力とは何ですか?
A:表面張力とは、液体の表面が強く、重さを支えることができる効果のことです。通常では浮かない小さなものが浮いたり、アメンボなどの昆虫が水面を走ったりすることができるのも表面張力の効果です。
Q:表面張力の原因は何ですか?
A:表面張力は、液体中の分子が互いに引き合う(凝集力)ことによって生じます。
Q:表面張力はどのような次元のものですか?
A:表面張力は、単位長さあたりの力、あるいは単位面積あたりのエネルギーという次元を持ちます。この2つは等価ですが、単位面積あたりのエネルギーに言及する場合、表面エネルギーという言葉を使いますが、これは液体だけでなく固体にも適用されるという意味で、より一般的な言葉です。
Q:表面張力は材料科学にどのような影響を与えるのでしょうか?
A: 材料科学では、表面張力は表面応力または表面自由エネルギーとして使用されます。
Q:凝集力は表面張力にどのように寄与していますか?
A:凝集は、液体中の分子を引き寄せることによって表面張力に寄与し、その表面で強い結合を作り、重量を支え、特定の物体や生物(例えば、アメンボ)が、他の方法ではできないような異なった相互作用をすることができるようになります。
Q: この性質は、他の液体の性質とどう違うのですか?
A: この特性は液体の他の特性とは異なり、物体がその内部や全体的な挙動を通してではなく、その表面でどのように相互作用するかに影響を与えるからです。
百科事典を検索する