チェックサム
チェックサムとは数字のことです。冗長性チェックの一種です。計算方法は様々です。チェックサムは、数字を書き留める際にエラーが発生していないかどうかをチェックする役割を果たします。最も単純な形では、数字を単純に足し算します。しかし、これは桁の入れ替えのエラーを検出することはできません。チェックサムを計算するより良い方法（アルゴリズム）としては、ハミングコード、周期的冗長性チェック、モジュール式算術などがあります。チェックサムの用途の一つは、口座番号が正しく入力されているかどうかをチェックすることです。
ポルトガルの銀行口座の識別子は、チェックサムがどのように機能するかを示す良い例です。21 桁の数字で構成されています。最初の19桁は銀行、支店、口座番号を識別します。最後の 2 桁は、モジュール式算術に基づく「mod 97」チェックサムの数字です。典型的なポルトガルの銀行口座番号は0002.0123.12345678901.54です。この数字には次のような意味があります。
· 桁の"0002"は銀行を表しています。
· 数字の"0123"は銀行の支店を表しています。
· 12345678901」という数字は口座番号を表しています。
· 数字の"54"はチェックサムを表します。
000201231234567890154（ドットのない銀行口座番号）を97で割ると、答えは207458809978249余り1となります。余りが「1」なので、銀行口座番号はおそらく正しいと思われます。もし、数字を書き込んだ人が桁を見落としたり、2桁を入れ替えたり、間違って書き込んだりした場合、残りの数字は「1」ではなかったでしょう。このような場合は、コンピュータがエラーを検出してエラーメッセージを表示する必要があります。
チェックサムが使用されるもう一つの場所は、コンピュータソフトウェアのシリアル番号です。
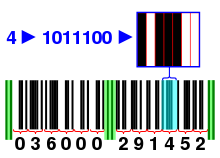
現代のEANバーコード。緑の部分はスペーサーと呼ばれています。彼らは番号のグループを分離します。各番号は、図のように7ビットでコード化されています。最初の11桁は製品番号です。最後の桁は、この場合は数字"2"で、チェックサムです。チェックサムは、偶数の位置と奇数の位置の和を3倍したものに10倍したものが0になるように加算されます。
質問と回答
Q:チェックサムとは何ですか?
A: チェックサムは冗長性チェックとして使用される数値です。番号を書き込む際に誤りがないことを確認するためのものです。
Q:チェックサムはどのように計算されるのですか?
A:チェックサムの計算方法は様々ですが、最も単純な方法は、単純に数字を足し算することです。しかし、これでは桁の入れ替わりなどのミスを検出することができません。
Q:チェックサムがどのように機能するかの例を教えてください。
A:ポルトガルの銀行口座の識別子は、チェックサムがどのように機能するかの良い例です。21桁の数字があり、最後の2桁はモジュラー演算に基づく「mod 97」チェックサムを表します。
Q:どのようにしてエラーを検出するのですか?
A:もしいずれかの桁が欠けていたり、入れ替わっていたり、間違って書かれていたりすると、余りは "1 "にはなりません。この場合、コンピュータはエラーを検出し、エラーメッセージを表示するはずです。
Q:チェックサムは、他にどのような場面で使用されていますか。
A:チェックサムは、コンピュータ・ソフトウェアのシリアル番号にも使用されています。
Q:チェックサムでエラーが検出された場合、どうなりますか?
A: もしチェックサムでエラーが検出されたら、コンピュータはそれを検出してエラーメッセージを出すはずです。
