曲線あてはめ
カーブフィッティングとは、一連のデータポイントに最もフィットする数学的な関数を構築することです。
曲線のフィットには、補間とスムージングがあります。補間の場合は、データに正確にフィットさせる必要があります。スムージングでは、データに近似的にフィットする「滑らかな」関数が構築される。関連するトピックとして回帰分析があるが、これはランダムな誤差を伴って観測されたデータにフィットした曲線にどの程度の不確実性が存在するかといった、統計的な推論の問題により焦点を当てている。
フィット曲線は、データの視覚化、データがない場合の関数の値の推測、2つ以上の変数の関係の要約などに使用できます。外挿とは、観察されたデータの範囲を超えてフィット曲線を使用することです。これは、観測されたデータを反映しているのと同様に、曲線を構築するために使用された方法を反映している可能性があるため、ある程度の不確実性を伴います。
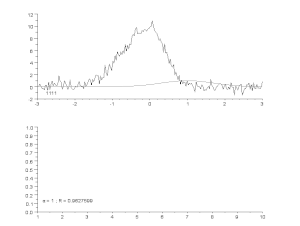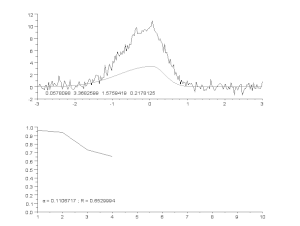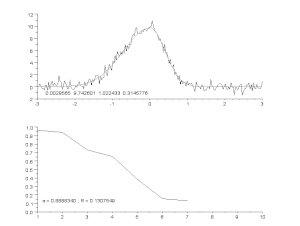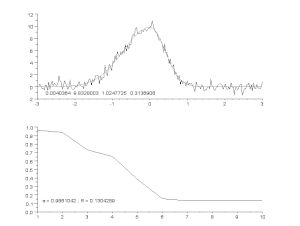
非対称ピークモデルによるノイズ曲線のフィッティングを、反復プロセス（Gauss-Newton algorithm with variable damping factor α）で行っている。 上：生データとモデル。 下：誤差の正規化二乗和の変化。
質問と回答
Q: カーブフィッティングとは何ですか?
A: カーブフィッティングとは、一連のデータポイントに最も適合する数学的関数を作成するプロセスです。
Q: カーブフィッティングの2つのタイプは何ですか?
A:カーブフィッティングには、補間と平滑化の2種類があります。
Q: 補間とは何ですか?
A: 補間はカーブフィッティングの一種で、データに正確にフィットすることが必要です。
Q: スムージングとは何ですか?
A: スムージングとは、カーブフィッティングの一種で、データに近似的にフィットする「滑らかな」関数を構築するものです。
Q: 回帰分析とは何ですか?
A: 回帰分析とは、ランダムな誤差を伴って観測されたデータにフィットする曲線にどれだけの不確実性が存在するかといった、統計的推測の問題に焦点を当てた関連トピックです。
Q: フィットした曲線にはどのような使い方がありますか?
A: フィット曲線は、データの可視化、データがない場合の関数の値の推測、2つ以上の変数間の関係の要約に使用することができます。
Q: 外挿とは何ですか?
A: 外挿とは、観測されたデータの範囲を超えてフィットカーブを使用することです。しかし、これは観測データを反映していると同時に、曲線を構築するために使用された方法を反映している可能性があるため、ある程度の不確実性を伴います。
