集合(数学)の定義:要素・空集合・演算・ラッセルのパラドックス
集合の基礎を要素・空集合・演算で図解解説。自己包含が招くラッセルのパラドックスもやさしく整理。数学入門から応用まで。
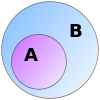
集合は数学の基本的な概念で、ある条件でひとまとめにした「要素(メンバー)」の集まりを指します。集合はその要素できまるため、同じ要素を持つ集合は同一とみなされます(拡張性の原理)。要素の記述には次のような表記を使います:x ∈ A は「x は集合 A の要素である」を意味します。
要素・表記・性質
集合の表し方としてよく使われるもの:
- {a, b, c} — 要素が a, b, c である集合。
- {x | 条件} — 条件を満たす全ての x を集めた集合(集合内包表記、集合わく)。
集合の基本的な性質:
- 順序は無関係:{a, b} = {b, a}。
- 重複は無意味:{a, a, b} = {a, b}。集合は同じ要素を複数回数えることはしません。
- 拡張性:2つの集合が同じ要素を全て持つならば、それらは同じ集合(A = B)。
空集合と基数
ある特定の集合として、要素を何も持たない集合を空集合と呼び、記号は ∅ または {} で表します。空集合は一意に定まります。集合の要素の個数を表す概念を基数(cardinality)といい、有限集合なら |A| でその要素数を表します。無限集合については可算無限・非可算無限などの区別があります。
集合の演算と構成
集合にはいくつかの基本的な演算があります:
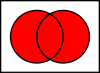
- 和集合(合併):A ∪ B は A または B の要素全体。
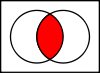
- 積集合(共通部分):A ∩ B は A と B 両方に属する要素。
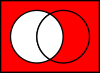
- 差集合:A \ B は A に属し B には属さない要素。
- 補集合:全体集合 U を定めれば、A の補集合は U \ A。
- 対称差:A Δ B = (A \ B) ∪ (B \ A)。
- べき集合:P(A) は A の部分集合全体の集合(要素は部分集合)。
- 直積(デカルト積):A × B は順序対 (a, b) 全体。これを使って関数や関係を集合として定義できます。
関数は一般に「ある集合から別の集合への写像」として定義され、集合論的には順序対の集合として表されます(各入力に対してちょうど一つの出力が対応する集合)。
部分集合と等号
集合 A が集合 B の部分集合であるとは、A のすべての要素が B に属することを意味し、記号 A ⊂ B または A ⊆ B を使います。等号 A = B は A ⊆ B かつ B ⊆ A のとき成立します。
注意すべきパラドックスと公理化
任意の条件で集合を作れると考えると、自己言及的な集合による矛盾(パラドックス)が生じます。たとえば、その手続き的な問題を示す代表例がラッセルのパラドックスに注意する必要があります。簡単に言うと「自分自身を要素に含まない集合すべての集合 R」を考えると、R が自分自身の要素であるか否かで矛盾が生じます。
このような問題を避けるために、現代の集合論では公理系による厳密化が行われます。代表的なものに次があります:
- Zermelo–Fraenkel 集合論(ZF)、選択公理を加えた ZFC:集合の構成や集合がどのように振る舞うかを公理で定め、ラッセル型の矛盾を回避します。
- タイプ理論や Von Neumann–Bernays–Gödel (NBG) 集合論など、別の形式化手法もあります。
公理化により「すべての条件で自由に集合を作れる」という素朴な原理(包含公理の無制限版)は制限され、集合が自分自身を要素に持てるかどうかや基礎性(well‑foundedness)などの性質も公理によって扱われます。逆に、非基礎的集合論(非 well‑founded set theory)では自分自身を要素に持つ集合を扱うこともあります。
例と応用
簡単な例:
- {1, 2, 3} は 1,2,3 を要素に持つ集合。
- P({1,2}) = {∅, {1}, {2}, {1,2}}。
- 直積 {1,2} × {a,b} = {(1,a), (1,b), (2,a), (2,b)}。
集合の概念は数学のほぼ全領域で基盤となっており、論理学、代数、位相空間、確率論、計算機科学(データ構造や型理論)など多くの分野で利用されます。

1894年、ゲオルク・カントール。カントールは、集合について語った最初の数学者である

カントールによる集合の定義。集合とは,私たちの直感や思考の対象である明確で別々のものmを全体(...)Mに集めたものであると理解することである.これらの対象は、Mの要素と呼ばれる。
表記方法
ほとんどの数学者は、集合について書くときに大文字のイタリック体(通常はローマ字)を使用します。集合の要素とみなされるものは、通常、小文字のローマ字で書かれます。
集合を表す方法のひとつに、カンマで区切って中括弧で囲んだメンバーのリストがあります。例えば
- X={1,2,3}は、メンバー1,2,3を持つ集合である。
もう一つの方法は、集合のメンバーについて何が真実であるかを示す声明で、次のようなものです。
- {x|xは自然数&x<4}。
口語では、それは"xが自然数でxが4未満であるようなすべてのxの集合 "である。
空集合は特殊な書き方をしています。
- ∅ {displaystyle \emptyset }.
オブジェクトaが集合Aのメンバーである場合は、次のように記述されます。
- a(A)。
口語では、つまり"a is a member of A"
セットで何をするか
の要素
袋の中にいろいろなものを入れることができる。後で、あるものが袋の中に入っているかどうかが、有効な質問となる。数学者はこれを「要素(element of)」と呼ぶ。あるものが袋の中に入っていれば、そのものは集合の要素である。この記号を∈ {displaystyle \in }という。
a∈A {displaystyle a\ in \mathbf {A} }.}
は{displaystyle a}
空集合
バッグと同じように、セットも空になることがあります。空のセットは、空のバッグのようなもので、中には何も入っていません。
セットの比較
2つのセットを比較することができます。これは、2つの異なるバッグを見るようなものです。同じものが入っていれば、それは同じです。
集合の基数
数学者が集合について話すとき、集合の大きさを知りたいと思うことがあります。これは,集合の中にいくつの要素があるか(バッグの中にいくつのアイテムがあるか)を数えることによって行われます.カージナリティは単純な数であることもある.空集合のカージナルは0である。{displaystyle \{apple,orange}}
2つの集合は、その要素を対にすることができれば、つまり、それぞれの集合から1つずつ2つの要素を結合することができれば、同じ基数である。集合 { a p p l e , o r a n g e } は、次のようになる。{displaystyle \{apple,orange}}



無限のカージナリティ
カーディナリティが数字でないこともある。集合は無限のカージナルを持つことがある。整数の集合は無限のカージナルを持つ集合である。無限の基数を持つ集合の中には、他の集合より大きい(基数が大きい)ものがある。たとえば、実数は自然数より多い。つまり,永遠に働いても,整数の集合と実数の集合を対にすることはできないのです.もしある集合が整数の集合と同じ基数を持つなら,それは可算集合と呼ばれる.しかし,もし集合が実数と同じ基数を持つなら,それは数えられない集合と呼ばれる.
サブセット
集合{a,b}と集合{a,b,c,d}を見ると、最初の集合の要素はすべて2番目の集合にも入っていることがわかるでしょう。
私たちはこう言います。{a,b} は {a,b,c,d} の部分集合である。
式にすると、次のようになります。
{ a , b } の部分集合⊆ { a , b , c , d } となります。{displaystyle \{a,b}subseteq \{a,b,c,d}}} となります。
Aのすべての要素がBの要素でもあるとき、AをBの部分集合と呼ぶ。
A ⊆ B {displaystyle A}
通常は "A is contained in B "と読みます。
例
すべてのシボレーはアメリカ車である。だから、すべてのシボレーの集合は、すべてのアメリカ車の集合に含まれる。
セットオペレーション
セットの組み合わせ方はさまざまです。
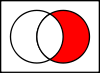
交差点
The intersection A∩B {displaystyle Acap B}
that are both in set A and in set B, all the elements that contains the all of the elements, in set B.
Aがすべての安い車の集合で、Bがすべてのアメリカ車の集合のとき
、A ∩ B {displaystyle Acap B}
ユニオン
The union A∪B {displaystyle Acup B}
that are in set A or in set B, all elements, contain the set that is
in set A or in set B.
この「または」は包含的論理和であり、集合Aと集合Bに含まれる要素も和集合に含まれる。
ちなみにこれは、交差点が和集合の部分集合であることを意味します。
( A∩B ) ⊆ ( A∪B ) {displaystyle (Acap B)\subseteq (Acup B)}.
Aをすべての安い車の集合、Bをすべてのアメリカ車の集合とすると
、A∪B {displaystyle Acup B}
コンプリート
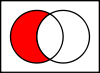
Complementには2種類の意味があります。
- Aの補集合は、Aのすべての要素を除いた宇宙Uである。
A C = U ∖ A {displaystyle A^{rm {C}}=U}{setminus A}
宇宙Uは、あなたが話すすべてのものの集合である。
Uをすべての車の集合、Aをすべての安い車の集合とすると
、AC 、すべての高い車の集合である。
- BにおけるAの相対補語は、Aの要素をすべて除いた集合Bである。
B ∖ A {displaystyle Bsetminus A} とする。 
呼ばれることが多い。
Aをすべての安い車の集合、Bをすべてのアメリカ車の集合とすると
、B ∖ A {displaystyle Bsetminus A}
車の例では、差分 A ∖ B {displaystyle Asetminus B}
特別セット
数学にとって非常に重要な集合があります。非常によく使われます。その1つが空集合です。これらの集合の多くは、以下のように黒板太字の書体で書かれています。特殊な集合は以下の通りです。
- P {displaystyle \mathbb {P} }.}
はすべての素数の集合を表します。
- N {displaystyle \mathbb {N} }.}
はすべての自然数の集合である。つまり、N {displaystyle \mathbb {N} } は、すべての自然数の集合である。}
N {displaystyle \mathbb {N} } = {1, 2, 3, ...} または、N {displaystyle \mathbb {N} } の場合もあります。}
= {0, 1, 2, 3, ...}.
- Z {displaystyle \mathbb {Z} }.}
はすべての整数(正、負、ゼロを問わない)の集合を表します。だから、Z {displaystyle \mathbb {Z} } は、すべての整数の集合を表す。}
= {..., -2, -1, 0, 1, 2, ...}.
- Q {displaystyle \mathbb {Q} }.}
はすべての有理数の集合(すなわち、すべての正・負分 の集合)です。つまり、Q = { a b : a , b∈Z , b ≠ 0 }となります。{displaystyle \mathbb {Q} =left}{{begin{matrix}{prac {a}{b}}}}end{matrix}}:a,b}in \mathbb {Z} ,bneq 0}{b}{prac {a}{b}{prac}{prac}}{prac}{prac}{prac}{prac}{prac}{prac}}} 0,bneq 0right}} である。
ここで、a と b は整数の集合に含まれ、b は 0 に等しくない。例えば、1 4∈Q {displaystyle {Threshold{matrix}{frac {1}{4}} end{matrix}} in \mathbb {Q}} は、1 4 ∈Q {displaystyle {Threshold{matrix}{FRAC {1}{4}}は、"0 "を意味し、"1 "を意味しない。}
and 11 6∈Q {displaystyle {}begin{matrix}{cfrac {11}{6}}}end{matrix}}in \mathbb {Q}} {displaystyle {}begin{matrix}{cfrac {11}{6}}}は "end{matrix}"である。}
.すべての整数aは分数a 1 {displaystyle {}begin{matrix}{cfrac {a}{1}}}end{matrix}}
として表現できるので、すべての整数がこの集合に含まれる。
- R {displaystyle \mathbb {R} } は、すべての実数の集合を表します。
はすべての実数の集合を表します。この集合にはすべての有理数とすべての無理数(π , {displaystyle \pi ,}
e , {displaystyle e,}
, √2など分数として書き直すことができない数)が含まれます。
- C {displaystyle \mathbb {C} }.}
はすべての複素数の集合を表します。
これらの数の集合はそれぞれ無限個の要素を持ち、P⊂N⊂Z⊂Q⊂R⊂C {displaystyle \mathbb {P} } </p\⑭Subset ͟Mathbb {N}\⑭Subset ⑯Mathbb {Z}\⑭Subset ⑯Subset ⑭Q\╱︎╱︎╱︎╱︎╱︎╱︎╱︎╱︎╱︎╱︎╱︎쇼}
集合に関するパラドックス
数学者のバートランド・ラッセルは、この集合の理論に問題があることを発見した。彼はこれを「ラッセルのパラドックス」と呼ばれるパラドックスで表明した。より実生活に近いわかりやすいものは、バーバー・パラドックスと呼ばれる。
理容師のパラドックス
あるところに小さな町があります。その町には床屋さんがあります。町の男たちはみんなヒゲが嫌いなので、自分で剃るか、床屋に行って床屋さんに剃ってもらうか、どちらかです。
したがって、理髪師自身について述べることができる。床屋は、自分でひげを剃らないすべての男のひげを剃る。床屋は、自分でひげを剃らないすべての男のひげを剃る。
ここでもちろん疑問が生じる。床屋は毎朝何をやって髭を剃っているのだろう?これはパラドックスである。
- 理容師が自分の髭を剃らない場合は、ルールに従って自分の髭を剃る(理容室に行って髭を剃ってもらう)。
- もし理髪師が本当に自分の髭を剃るのであれば、上にあげた規則に従って、自分の髭を剃ることはない。
質問と回答
Q:セットとは何ですか?
A: 集合は数学の概念です。集合はメンバー(要素とも呼ばれる)から構成され、そのメンバーによって定義されるため、同じメンバーを持つ2つの集合は同じものである。
Q:集合は、同じメンバーを複数回持つことができますか?
A:いいえ,集合は同じメンバを複数回持つことはできません.
Q:集合では順序が重要ですか?
A:いいえ、集合において順序は重要ではありません。集合のメンバーには、集合そのものも含め、何でもなり得ます。
Q:集合がそれ自身のメンバーである場合、どうなりますか?
A:集合がそれ自身のメンバーである場合,ラッセルのパラドックスのようなパラドックスが起こり得ます.
Q:集合にとって重要なのは,メンバーシップだけですか?
A:はい,メンバーシップは集合にとって重要な唯一のものです.
Q:2つの集合が等しいかどうかは、どのようにしてわかるのですか?
A:2つの集合が等しいのは、同じメンバーを持っている場合です。
百科事典を検索する