関数 (数学)
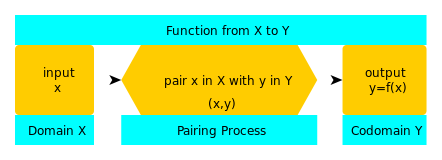
数学では、関数とは、入力が与えられたときに出力を生成する数学的なオブジェクトのことです。
関数は機械のようなもので、xの値を取り、出力yを返します。yが持つことのできるすべての値を含む集合をコドメインと呼びます。
そうなると、yはxの関数であり、y =f(x)と書くことになる。
(XからYへの関数)を使って、ドメイン(x)、コドメイン(y)、ペアリングプロセス(矢印)の3つの部分を表現します。
関数の例は f(x)=x+1 自然数x {\ style x
} (0,1,2,3...)を入力として与えて 自然数y {\ style y}を得る。
これは x {displaystyle x} +1 (1,2,3,4...) 関数という考え方は、様々な可能性をカバーするために設定されている。関数は方程式である必要はない。主な考え方は、たとえ非常に複雑なプロセスであっても、入力と出力が何らかの形でペアになっているということである。
メタファー
テーブル一覧表
インプットとアウトプットを写真のような表にまとめることができます。
グラフ
図では、2と3がcとペアになっているのがわかるが、これは反対方向には許されないことで、2はcとdを出力することができない。すべてのf ( x ) {displaystyle f(x)}の
(図中のcとd)は、通常、f {\displaystyle f}
の画像集合と呼ばれ、画像集合は、コドメ インの全てであってもよいし、そうでなくてもよい。画像集合を持つコドメインの部分集合Aはf(A)であると言える。入力と出力に順序があれば，それらをグラフにプロットするのは簡単である．
これにより、2と3の両方がペアになっていることになりますが、他の方向には許されていませんので、コドメインの間でも作ることができます。コドメインの部分集合Aが画像集合であるという結論はF(A)である。
歴史
1690年代にゴットフリート・ライプニッツとヨハン・ベルヌーリは、関数という言葉を文字で挟んで使っていたので、現代の概念は微積分と同時に始まった。
1748年にレオンハルト・オイラーは"可変量の関数とは，可変量と数または定数量とのいかなる方法でも構成される分析式である。この定義はかなり広く適用され，ある量が他の量によって決定され得るすべての方法を含んでいる．したがって、xが可変量を表すならば、何らかの方法でxに依存するか、それによって決定されるすべての量は、xの関数と呼ばれます」というのは非常に現代的です。
通常、ディリクレは20世紀後半まで学校で使われていたバージョンでクレジットされています。"yは変数xの関数であり，区間a < x < bで定義され，この区間内の変数xのすべての値に変数yの確定値が対応しているならば，この対応がどのような方法で確立されるかは無関係である"
1939年、BourbakiはDirichletの定義を一般化し、入力と出力の間の対応として定義の集合論的なバージョンを与えた；これは1960年頃から学校で使用されていた。
最後に、1970年にブルバキは、トリプルf = ( X , Y , F ) {displaystyle f=(X,Y,F)}として現代的な定義を与えた。
F ⊂ X × Y , ( x , f ( x ) ) とすると∈ (i.e.e. f : X → Y {displaystyle f:Xto Y} and F = { (x , f (x 
) ) } (i.e. f : X → Y {displaystyle f:Xto Y} and F = { (x , f (x ) ) )| x ∈X , f ( x )∈Y } ←これは、「x ∈X」と「f ( x )∈Y」の関係です。♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪
).
機能の種類
- 初等関数 - 学校で普通に習う関数：分数、平方根、正弦関数、余弦関数、接関数、その他いくつかの関数。
- 非要素関数 - ほとんどの関数は学校で習わない演算（＋や-、累乗など）を使わない。多くの積分は非要素関数である．
- 逆関数 - 別の関数を元に戻す関数．例：F(x)がf(x)=yの逆数ならば，F(y)=x．すべての関数が逆関数を持つわけではありません．
- 特殊な関数。名前を持つ関数。例：サイン、コサイン、タンジェントなど。f(x)=3x (xの3倍)のような関数は特殊関数とは呼ばない．これらの関数には，初等関数，非初等関数，逆関数があります．
質問と回答
Q:数学でいう関数とは何ですか?
A:数学における関数とは、入力が与えられたときに出力を生成するオブジェクトのことで、数値やベクトルなど、集合の中に存在しうるものである。
Q:関数に関連する2つの集合とは何ですか?
A:xが持ちうるすべての値を含む集合をドメインと呼び、yが持ちうるすべての値を含む集合をコドメインと呼びます。
Q:関数はどのように表記されることが多いですか?
A:関数はしばしばf，g，hのようなイタリック文字で表記されます．
Q:関数はどのように表現するのですか?
A:関数はy = f(x)で表されます．fは関数の名前，f : X → Y（XからYへの関数）は関数のドメイン（X），コードメイン（Y），ペアリング処理（矢印）の3つを表します．
Q:関数の例を教えてください。
A:関数の例としては，f(x) = x + 1がある．自然数xを入力として与えれば、x＋1の自然数yが得られる。例えば、fの入力に3を与えると、4が出力されます。
Q:すべての関数が方程式である必要があるのでしょうか?
A:いいえ、すべての関数が方程式である必要はありません。関数の主な考え方は、入力と出力が何らかの形で組み合わされることです-たとえそれが非常に複雑であったとしても。
