楕円
楕円とは、楕円や扁平な円のような形をしています。
幾何学では、楕円とは、円錐体と平面との交点が閉じた曲線になるような平面曲線のことをいいます。
円は楕円の特殊なケースで、切断面が円錐の軸に垂直な場合に得られます。楕円もまた、平面のすべての点の軌跡であり、2つの固定点までの距離が同じ定数に加算されます。
円には焦点と呼ばれる中心が一つありますが、楕円には焦点が二つあります。
楕円とは、グラフ上のすべての点のうち、2つの点からの距離の和が同じである点のことです。例えば、厚紙にピンを2本入れて、その2本の周りに紐の輪を作り、その輪の中に鉛筆を入れて、紐が全方向に切れないようにできるだけ遠くまで引っ張ると楕円ができます。惑星の軌道は楕円で、一方の焦点には太陽があり、もう一方の焦点には何もありません。
楕円の方程式は次のようになる。( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{frac {(y-k)^{2}}{b^{2}}}=1
}
ここで、楕円の中心は(h,k)である。2aは、長い方の痩せた側の
両端からの長さである。2bは短い方の2つの端からの長さです。a²-b²=c²は、cの場合は焦点と中心との間の長さである。
円錐と平面の交点として得られる楕円。
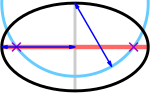
病巣（紫の十字）は、長軸（赤）と短軸（灰色）の端を中心とした半長軸（青）と等しい半径の円（青）の交点にあります。
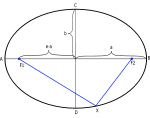
楕円とその特性。
質問と回答
Q:楕円とは何ですか?
A: 楕円は、楕円または円を平らにしたような形状です。幾何学では、円錐と平面が閉曲線を作るように交わった結果の平面曲線のことです。
Q:楕円はどのように作るのですか?
A: 楕円は、厚紙に2本のピンを刺し、その2本のピンの周りに紐を輪にして、その輪の中に鉛筆を入れ、紐が切れない範囲で四方に引っ張ることで作ることができる。
Q:円は何の特殊な場合なのですか?
A:円は楕円の特殊例で、切断面が円錐の軸に垂直である場合に作られます。
Q: 楕円の焦点はいくつあるのですか?
A: 楕円の焦点は2つです。
Q:楕円を記述する方程式は何ですか?
A: 楕円の方程式は (x - h)²/a² + (y - k)²/b² = 1 ここで、hとkは楕円の中心、2aは長い方の細い辺の両端からの長さ、2bは短い辺の両端間の長さを表します。Cは焦点と中心間の長さを表し、A²-B²=C²となる。
Q: 楕円軌道の例はどこにある?
A:楕円軌道は、太陽を1つの焦点とする惑星で見ることができます。
