円（数学）とは｜定義・半径・直径・円周率π・円周・面積の公式

円の定義から半径・直径・円周率π、円周・面積の公式まで図解と例でわかりやすく解説。基礎から応用まで学べる円の数学ガイド。

著者: Leandro Alegsa

23-09-2025 13:13

円は丸い二次元の形状である。円の端にあるすべての点は、中心から同じ距離にある。図形としては、境界だけを表す「円周」と、その内部を含む「円板（円盤）」を区別して扱うことが多い。

円の半径は、円の中心から側面の点までの直線である。数学者は円の半径の長さをrという文字で表す。半径は円の大きさを決める基本量で、長さの単位（cm, m など）で表す。円の中心とは、円の中心の点のことである。

円の直径（「ずっと横切る」という意味）は、円の片側から反対側に向かって、円の中心を通る直線です。数学者は、この直線の長さにdという文字を使います。円の直径は半径の2倍に相当する（dは2倍のrに相当）。

♪ d = 2 r {displaystyle d=2 r} ♪ ♪ $d=2\ r$

円の円周（「一周する」という意味）とは、円の中心を回る線のことである。数学者はこの線の長さにCの文字を使います。円周の長さは直径や半径と関係があり、次の重要な定数を用いて表されます。

πという数字（ギリシャ文字のπと書かれています）は非常に便利な数字です。これは円周の長さを直径の長さで割ったものです（πはCをdで割ったものに等しい）。分数としてのπは約²²⁄₇または335/113（どちらか近い方）に相当し、数としては約3.1415926535になります。πは無理数であり、さらに超越数であることが知られています（すなわち有限個の代数的操作だけでは正確に表せない）。歴史的には円周率を求めるために多くの近似法や無限級数、数値計算法が発展しました。

円周と直径の関係から、円周の公式は次のように表せます：C = π d = 2 π r。この式は円の大きさ（半径や直径）から円周の長さを直接計算するために使います。たとえば、半径が3 cm の円では、円周は C = 2π×3 ≈ 18.85 cm になります。

円の内側の面積（円が囲む領域の面積）は、半径を使って表すと次の公式になります：A = π r²（元の文では小文字のaと表記されていますが、ここでは大文字のAで面積を示すことが多いです）。単位は平方センチメートル（cm²）や平方メートル（m²）などです。例として半径が3 cm の円の面積は A = π×3² = 9π ≈ 28.27 cm² です。面積公式の直感的な説明としては、円を非常に細かい同心円状の輪に分けて長方形に近い形へ並べ替える（あるいは極座標や積分を用いる）方法があります。

角度・弧・扇形（せんけい）に関する公式

中心角をθ（ラジアン）とすると、その角に対応する弧長 s は s = r θ で表される。θ が度数法（°）で与えられる場合はラジアンに変換する必要がある（θrad = θ° × π/180）。
同じ中心角θ（ラジアン）の扇形の面積は S = (1/2) r² θ である。これらは円周や面積の公式とラジアンの定義から直接導ける基本公式です。

円に関するその他の用語と性質（簡単なまとめ）

弦（chord）: 円周上の2点を結ぶ線分。直径は最長の弦で、常に中心を通る。
接線（tangent）: 円に1点だけ接する直線。接点での接線はその点における半径と直交する。
弧（arc）: 円周の一部分。長さは弧に対応する中心角で決まる（s = r θ）。
対称性: 円は中心を中心とする任意の回転に対して不変であり、無限の回転対称性を持つ。

計算例

半径 r = 5 cm の円: 円周 C = 2πr = 10π ≈ 31.4159 cm、面積 A = πr² = 25π ≈ 78.5398 cm²。
直径 d = 8 m の円: 半径 r = d/2 = 4 m、円周 C = πd = 8π ≈ 25.1327 m、面積 A = πr² = 16π ≈ 50.2655 m²。

円は幾何学だけでなく、物理学・工学・測量・天文学・コンピュータグラフィックスなど多くの分野で基本的かつ重要な役割を果たします。上に示した公式や性質を理解しておくと、円に関する多くの問題を簡潔に解くことができます。

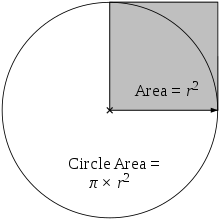
円の面積は、灰色の正方形の面積のπ倍に相当します。

円

πの計算

πは、大きな円を描いて、その直径(d)と円周(C)を測ることで測ることができます。これは、円の円周は常に直径のπ倍であるからです。

π = C d {displaystyle ﾟ ={\frac {C}{d}}}}} $\pi ={\frac {C}{d}}$

πは数学的な方法だけで計算することもできます。πの値を計算するために用いられるほとんどの方法は，数学的に望ましい性質を持っています。しかし，三角法や微積分を知らないと理解するのは難しいです．しかし、グレゴリー・ライプニッツ級数のこの形式のように、非常に簡単な方法もあります。

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯⋯ {\displaystyle \pi ={\frac {4}{1}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}-{\frac {4}{9}-{\frac {4}{11}cdots } }。 $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots$

この系列は書きやすく、計算しやすいのですが、なぜπに等しいのかがわかりません。すると、ピタゴラスの定理で計算された原点からの距離dがrよりも小さい点(x,y)は、その円の内側になります。

d = x 2 + y 2 {displaystyle d={ {x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

円の内側の点の集合を見つけることで、円の面積Aを推定することができます。円の面積Aは半径の2乗のπ倍なので、πは次のようにして近似することができます。

π = A r 2 {displaystyle pi ={\frac {A}{r^{2}}}} $\pi ={\frac {A}{r^{2}}}$

質問と回答

Q:円とは何ですか?

A:円は丸い二次元の形である。円の縁にあるすべての点は、中心から同じ距離にある。

Q:数学者は円の半径の長さを表すのに何を使うか?

A:数学者は円の半径の長さを表すのにrという文字を使う。

Q:円の中でOと書かれるものは何ですか?

A:円の中心はしばしばOと書かれる．

Q:円の直径はどのくらいですか?

A:円の直径（「ずっと」という意味）は、円の片側から反対側へ、そして円の中心を通る直線です。半径の2倍に等しい（dはrの2倍に等しい）。

Q:数学者は円周を表すのにどのような文字を使うのですか?

A:数学者は円周をCで表し、「全周」を意味する。

Q:円の内側の面積はどのように計算するのでしょうか?

A:円の中の面積Aは、その半径に自分自身を掛け、さらにًを掛けることで計算できます（Aはً×r×rに等しい）。

百科事典を検索する