周波数とは：定義・単位（Hz）・波長との関係、電磁波と音波の例
周波数とは何かをわかりやすく解説。Hzの意味、波長との数式的関係、光・電波・赤外・マイクロ波や音波の実例と速度の違いを図解で学べる。
周波数とは、ある現象（波や振動など）が単位時間あたりに繰り返される回数を表す物理量です。周期と対応する概念で、周期T（1周期に要する時間）と周波数fは逆数の関係にあります：f = 1 / T。周波数の国際単位系（SI）での単位は1秒あたり1回を表す「ヘルツ（Hz）」で、記号はHzです（1 Hz = 1 s⁻¹）。
基礎的な式と波長との関係
波の速度をv、波長をλ（ラムダ）、周波数をfとすると、基本式は次のとおりです（波が一定の速度で伝わる場合）：
f = v / λ {displaystyle f=v/\lambda } 
ここでvは波の伝播速度、λ
（λ）は波長です。光波や電磁波の特別な場合は、真空中での速度が光速cになるため、式は次のようになります：
f = c / λ {\displaystyle f=c/\lambda }
ここでcは光速で（真空中で約 2.998×10^8 m/s）です。媒体の屈折率nを用いると、媒体中の光の速度はv = c / nとなり、同じ周波数であれば媒体中での波長はλ = v / fに従って短くなります。
周波数の単位と接頭辞
- ヘルツ（Hz）：1 Hz = 1 s⁻¹
- よく使われる接頭辞例：kHz（キロヘルツ, 10^3 Hz）、MHz（メガヘルツ, 10^6 Hz）、GHz（ギガヘルツ, 10^9 Hz）、THz（テラヘルツ, 10^12 Hz）など。
電磁波と音波の具体例
物理では、波の周波数は「1秒間にある点を通過する波紋の数のこと」と表現されます。ヘルツ（記号Ｈｚ）は周波数の単位です。
電磁波の例としては、光波、電波、赤外線、マイクロ波、ガンマ波などがあります。すべての電磁波は、真空中では光の速度で移動しますが、物質中では屈折率により速度が遅くなります。
音波などの機械的波は、物質（空気や水、固体）を媒介して伝わり、真空中を伝わることはできません。たとえば空気中の音速は温度や圧力で変化しますが、室温（約20 ℃）では約343 m/s、液体や固体ではさらに速くなることがあります。
生体や技術での周波数の例
- 人間の可聴域：およそ20 Hz ～ 20 kHz（年齢や個人差あり）
- AMラジオ帯：数百 kHz、FMラジオ帯：88 ～ 108 MHz
- 携帯電話やWi‑Fi：数百 MHz ～ 数 GHz帯域
- 可視光：波長約380 nm ～ 750 nmに対応し、周波数に換算するとおよそ400 THz ～ 790 THz（赤は周波数が低く、青は高い）
周波数とエネルギー、角周波数
光子1個のエネルギーEは周波数に比例し、プランク定数hを用いて次の関係があります：E = h f（h ≈ 6.626×10^−34 J·s）。したがって周波数が高いほど光子1個あたりのエネルギーは大きくなります（例：紫外線やX線は可視光より高エネルギー）。
振動や波動の解析では角周波数ω = 2π fもよく使われます。角周波数はラジアン単位での周期運動の速さを表します。
伝播速度と分散
多くの媒質では波の速度が周波数に依存することがあり、これを「分散」と呼びます。分散がある場合、波群の包絡線が伝わる速度（群速度）と個々の波面の速度（位相速度）が異なることがあります。通信や光学設計ではこの性質が重要です。
まとめ（ポイント）
- 周波数fは「単位時間あたりの繰り返し回数」で、単位はヘルツ（Hz）
- 波長λと速度vの関係：f = v / λ。真空中の光ではf = c / λ。
- 周波数は音や電磁波の性質（伝播速度、エネルギー、透過・吸収など）に深く関わる基本量である。
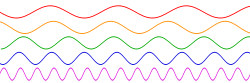
時間が経過すると、ここでは、水平軸上で左から右に移動すると、5つの正弦波は、異なるレート（または比率）で定期的に変化するか、またはサイクルします。赤色の波（上）は周波数が最も低く（つまり、最も遅い速度でサイクル）、紫色の波（下）は最も高い周波数（最も速い速度でサイクル）を持っています。
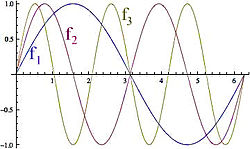
3つの異なる周波数を持つ正弦波 f.
電磁波の可視化
電磁波の種類によって周波数が異なります。
例
これを可視化する一つの方法は、同じ速度で走行する2つの列車があったとして、一方の列車の方がもう一方の列車よりも車両の大きさが小さい場合です。誰かが動かないもの、例えば標識のようなものを選んで、各列車ごとに1秒間に何台の列車が標識を通過したかを数えれば、各列車の通過頻度を知ることができます。車両が小さい電車の方が、車両が大きい電車よりも1秒間に看板を通過する車両の数が多いので、看板を通過する車両の数や頻度が違ってきます。1秒間に何両の車両が標識ポストを通過したかを知り、列車の速度を知ることで、各列車の車両の大きさを数学的に求めることができました。
例えば、電車が秒速10マイルで動いていて、1秒間に10両の電車が通過したとすると、1両の電車の長さは1マイルになります。もう一方の電車が毎秒10マイルで動いていて、1秒間に20両の電車が通過した場合、各電車の車の長さは1マイルの1/2であることがわかります。この例では、電磁波の周波数を知ることで波長がわかることを示しています。すべての電磁波は光の速度で移動するので、c = v (ラムダ) ここで、vは周波数であり、ラムダは波長であり、cは光速です。したがって、周波数を表現する別の方法は、周波数がラムダの上にcであると言うことです。
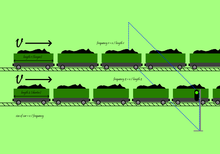
同じ速度で移動する2つの異なる列車
質問と回答
Q:頻度とは何ですか?
A:頻度とは、ある事象が一定時間内に何回繰り返されるかを示すものです。
Q:周波数を表す単位は何ですか?
A:周波数の単位はヘルツ（記号Hz）です。
Q:周波数と波長の関係を表す式は?
A:周波数と波長の関係は、vを速度、λを波長とすると、f=v/λの式で表されます。
Q: 光波の場合、この式はどのように変わるのですか?
A:光波の周波数を表す式は、f=c/λ（cは光速）です。
Q:真空中の電磁波はどのくらいの速さで伝わるのでしょうか?
A:すべての電磁波は、真空中では光速で伝わる。
Q:他の媒質中ではどのくらいの速さで伝わるのか?
A: 電磁波は真空以外の媒質中を伝わるとき、より遅い速度で伝わります。
Q:電磁波の例はあるのですか?
A:光波、電波、赤外線、マイクロ波、ガンマ線などがあります。
百科事典を検索する