ヘヴィサイド関数（単位ステップ関数）入門：定義・性質・デルタ関数との関係

ヘヴィサイド関数（単位ステップ）の定義・性質を平易に解説し、デルタ関数との関係や応用例まで図解でわかる入門ガイド。

著者: Leandro Alegsa

08-11-2025 19:30

Heaviside関数Hは、負の入力に対して0、正の入力に対して1の値をとる非連続関数である。

制御理論の数学で、ある時刻にスイッチが入り、無期限にスイッチが入ったままになる信号を表す関数である。英国人オリバー・ヘヴィサイドにちなんで命名された。

Heaviside関数はDiracδ関数の積分であり、H′＝δである。H′ = δ と書かれることもある。

定義と表記

一般に単位ステップ関数（Heaviside関数）は次のように定義される：

H(t) = 0, t < 0
H(t) = 1, t > 0

t = 0 における値 H(0) は文献や用途によって扱いが分かれます。対称性や変換の都合から H(0) = 1/2 と定めることが多く、特にフーリエ変換や分布論的扱いで自然になりますが、信号処理や離散化では 0 または 1 とすることもあります。どの定義を採るかは文脈に合わせて明示してください。

基本的性質

加法・平行移動：H(t − t0) は時刻 t0 で「入る」信号を表す。
スケーリング：H(a t) は a の符号で入り方が変わる（a > 0 なら単に速さの違い）。
掛け算による因果化：任意の信号 x(t) に対し x(t)H(t) は因果信号（t < 0 で 0）を表す。
積分と微分（分布として）：H(t) は分布（一般化関数）として扱うと微分がデルタ関数になる。形式的に H′(t) = δ(t)（分布の等式）であり、逆に δ(t) は H(t) の弱導関数とみなせる。

デルタ関数との関係

デルタ関数 δ(t) は「無限に鋭い」インパルスで、次の関係が成り立つ：

∫_{-∞}^{t} δ(τ) dτ = H(t) （積分の定義により、任意の t に対して上限までの累積がステップになる）
分布としての微分：dH/dt = δ

これらは通常の関数の微分・積分とは異なり、分布論の枠組みで厳密に扱われます。実際にはデルタは関数ではなく測度や線形汎関数である点に注意してください。

連続近似（正則化）の例

実用上は連続関数の極限としてステップを表現することが多いです。代表的な近似：

シグモイド関数： Hε(t) = 1 / (1 + e^{-t/ε}), ε → 0+
アークタン関数： Hε(t) = 1/2 + (1/π) arctan(t/ε)
ローレンツ形やガウス関数を積分して得る形

これらの連続化を用いると、数値計算や数値微分でデルタに近い挙動を扱いやすくなります。

変換（ラプラス・フーリエ）

ラプラス変換：因果型の単位ステップ H(t) の片側ラプラス変換は L{H(t)} = 1/s （Re(s) > 0）となります（H(0) の取り扱いにより補正が必要な場合あり）。
フーリエ変換（分布として）：F{H(t)} = P.V.(1/(jω)) + π δ(ω)、ここで P.V. は主値（principal value）を表します。この形は H を通常の関数としてではなく分布として扱うために現れます。

用途と例

制御・信号処理：スイッチやステップ入力（単位ステップ応答）を表す基本要素。伝達関数の単位ステップ応答から系の時定数や過渡特性を調べる。
微分方程式の解法：強制項としてのステップ入力を扱うとき、初期条件を含めた解の導出に用いる。
畳み込み：δ と H の畳み込みは H そのものである（δ は単位元）。また任意の信号 x(t) と H(t) の畳み込みは causal な積算を表す。
例：因果正弦波は sin(t)H(t)。

注意点と実務的アドバイス

t = 0 での値（0, 1, 1/2）を明示する。数式操作や離散化で結果が変わることがあるため、定義を最初に決めておく。
デルタ関数やフーリエ変換を扱うときは「分布」としての取り扱いを意識する。無理に通常関数のルールを適用すると矛盾を招く。
数値シミュレーションでは連続近似を使い、ε を系の時定数やサンプリング周期に合わせて選ぶとよい。

以上がHeaviside関数（単位ステップ関数）の基本的な定義・性質・デルタ関数との関係の概観です。用途に応じて定義の細部（特に t = 0 における値）を明確にしてから議論を進めると混乱が少なくなります。

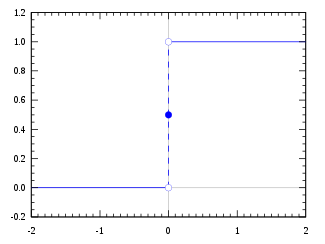
Heavisideステップ関数、ハーフマキシマム規約使用時

離散形式

また、Heavisideステップ関数の別形式を離散変数nの関数として定義することも可能である。

H [ n ] = { 0 , n < 0 1 , n ≥ 0 {displaystyle H[n]={}begin{cases}0,&n<0}1,&ngeq 0}end{cases}}}. $H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}$

ここで、nは整数である。

または

H ( x ) = lim z → x - ( ( | z | / z + 1 ) / 2 ) {displaystyle H(x)=lim _{zrightarrow x^{-}}((|z|/z+1)/2)} } ｛Displaystyle H(x)=lim _{zrightarrow x^{-}}((|z|/z+2)/2) $H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)$

離散時間単位インパルスは、離散時間ステップの最初の差分である

δ [ n ] = H [ n ] - H [ n - 1 ] .} $\delta \left[n\right]=H[n]-H[n-1].$

この関数は、クロネッカーデルタの累積和である。

H [ n ] = ∑ k = - ∞ n δ [ k ] {displaystyle H[n]=Thum _{k=-Θinfty }^{n}delta [k]\,} } {displaystyle H[n]=Thum _{k=-Θinfty }^{n}delta [k]</displaystyle $H[n]=\sum _{k=-\infty }^{n}\delta [k]\,$

どこ

δ [ k ] = δ k , 0 {displaystyle \delta [k]=Thresholddelta _{k,0}, } }. $\delta [k]=\delta _{k,0}\,$

は離散単位インパルス関数である。

表現方法

多くの場合、Heavisideステップ関数の積分表現が有効である。

H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ 1 τ + i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ 1 τ - i ϵ e i x τ d τ .{H(x)=Thinklim _{Epsilon \to 0^{+}}-{1 \over 2pi \mathrm {i}.}int _{-̮infty}^{1 ┣︎┣︎┣︎┣︎┣︎┣︎┣︎쇼\Ίτανα για για για^{-͈ω-͈ˋ} xtau } }mathrm {d}.\Ίτ = ΊLim _{epsilon Ίto 0^{+}}{1 τover 2 π Ίmathrm {i} Ίτ = ˊᵕˋ}int _{-͈༝}^{ ⑅⃝ ⑅⃝ ⑅⃝ -⑅⃝mathrm {i} ⑅⃝mathrm {i｝\Ίτανα για για για^{mathrm {i} xtau } } }mathrm {d} .\tau .} $H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau .$

H(0)

0における関数の値は、H(0)=0、H(0)=1/2、H(0)=1として定義することができる。

H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0.{\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} $H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}$

質問と回答

Q: Heaviside関数とは何ですか?

A: Heaviside関数は負の入力に対して値が0、正の入力に対して値が1となる非連続関数です。

Q: なぜ制御理論でHeaviside関数が使われるのですか?

A: ヘビサイド関数は、制御理論において、指定された時間にスイッチが入り、無期限にスイッチが入ったままになる信号を表すために使用されます。

Q: Heaviside関数の名前の由来となった人物は誰ですか?

A: Heaviside関数は英国人Oliver Heavisideにちなんで命名されました。

Q: Heaviside関数とディラック・デルタ関数の関係は?

A: Heaviside関数はディラック・デルタ関数の積分です: H′(x)=δ(x).

Q: 正の入力に対してHeaviside関数は何を出力するか?

A: Heaviside関数は正の入力に対して1を出力する．

Q: Heaviside関数は負の入力に対して何を出力するか?

A: Heaviside関数は負の入力に対して0を出力する。

Q: Heaviside関数はどのような関数か?

A: Heaviside関数は非連続関数です。

百科事典を検索する