積分とは — 微分との関係、記号、リーマン和、面積・体積の求め方

積分とは何かを図解でやさしく解説。リーマン和・記号の由来、微分との基本定理、面積や体積の求め方まで丁寧に紹介。

著者: Leandro Alegsa

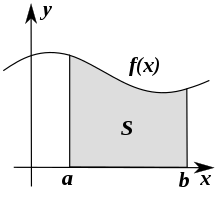
微積分では、積分とは方程式のグラフの下の空間のことである（「曲線の下の面積」と言われることもある）。積分は微分の逆であり、微分積分の反対語である。微分とは、曲線の急峻さ（または「傾き」）の変化率のことである。また、「積分」という言葉は、「整数に関連する」という意味の形容詞として使われることもあります。

積分の記号は、微積分では、∫ {displaystyle \int _{\,}^{\,}}を{\displaystyle \int _{\,}^{\,}}背の高い文字"S"に見立てたものである。この記号はゴットフリード・ウィルヘルム・ライプニッツが最初に使った。(summa、ラテン語でsumの意味)で、y = f(x)のような方程式でカバーされる面積の総和を意味します。

積分は 問題に単位を乗算しようとするときに 役に立ちます。例えば、レートの問題ならば、 ( distance time ) {\displaystyle \left({\frac {\text{distance}}{\text{time}}}right)}。{\displaystyle \left({\frac {\text{distance}}{\text{time}}}\right)}が距離だけで答えが必要な場合は、時間を基準にして積分するのが一つの解法だ。(distance time) × time (distance time)で 時間を打ち消すように 時間を掛けていくことだ。{\displaystyle \left({\frac {\text{distance}}{\text{time}}}\right)\times {\text{time}}}.これは、レートグラフの小さなスライスを一緒に追加することで行われます。スライスの幅はゼロに近いですが、それらを永遠に足し合わせると全体になります。これはリーマン和と呼ばれています。

これらのスライスを足し合わせると、最初の式の導関数となる式が得られます。積分は、たくさんの小さなものを手で足し合わせるようなものです。それは、1 + 2 + 3 + 4を足した和のようなものだ....+ n {displaystyle 1....} .{\displaystyle 1+2+3+4....+n}間にあるすべての小数と分数を足さなければならないことだ。

固体の体積を求めるときに、積分が役立つもう一つの方法があります。これは、幅があるまで、固体の二次元（幅のない）スライスを永遠に一緒に追加することができます。これは、オブジェクトが3次元になったことを意味します：元の2つと幅です。これは、記述されている三次元物体の体積を与えます。

積分の種類と記法

定積分は区間 [a, b] における面積のような「有限の合計」を表します。記号では通常

∫_a^b f(x) dx

の形で書き、これは関数 f(x) を区間 a から b まで積分することを意味します。ここで dx は独立変数 x に関する「非常に小さな幅」を表す記号です。

不定積分（原始関数、または反導関数）は、ある関数 f の導関数が f になるような関数 F を求める操作です。記法は

∫ f(x) dx = F(x) + C

で、C は積分定数（任意定数）です。

微積分の基本定理

微積分の基本定理は積分と微分の関係を明確にします。主に二つの部分があります：

  • （第一部）F(x) = ∫_a^x f(t) dt と定義すると、F'(x) = f(x) が成り立ちます。すなわち、積分を x まで累積した関数を微分すると元の関数に戻る。
  • （第二部）もし F'(x) = f(x) となる原始関数 F が存在すれば、定積分は評価の差で求められます：

    ∫_a^b f(x) dx = F(b) - F(a)

リーマン和と極限

定積分はリーマン和の極限として定義できます。区間 [a, b] を n 個の小区間に分割して、それぞれの区間で関数値 f(x_i*) に区間幅 Δx_i を掛けた和

Σ f(x_i*) Δx_i

を取ります。分割を細かくしていき（max Δx_i → 0）、その極限が存在すればそれが定積分 ∫_a^b f(x) dx です。これにより「無限に小さい幅の長方形を無限に足す」直感が厳密化されます。

面積・体積の求め方（応用）

  • 面積：x 軸と曲線 y = f(x)、区間 [a, b] の下の面積は ∫_a^b f(x) dx。二つの曲線 y = f(x) と y = g(x) の間の面積は ∫_a^b |f(x) − g(x)| dx で与えられます（通常は上下どちらが上かを確認して差を取ります）。
  • 体積（切片法）：立体を垂直な薄い断面（面積 A(x)）で表せる場合、体積 V は ∫_a^b A(x) dx で求められます。円盤法（ディスク）、ワッシャー法（穴あき円盤）、円柱殻法（シェル法）などが代表的です。
  • 仕事や距離：速度 v(t) の積分 ∫ v(t) dt は変位を与え、力 F(x) を距離に沿って積分すると仕事 W = ∫ F(x) dx になります。

積分の性質と計算法

  • 線形性：∫ (a f(x) + b g(x)) dx = a ∫ f(x) dx + b ∫ g(x) dx。
  • 区間分割：∫_a^c f(x) dx + ∫_c^b f(x) dx = ∫_a^b f(x) dx。
  • 置換積分（チェーンルールの逆）：x = φ(u) の変換を使って積分を簡単にする方法。
  • 部分積分（積の微分法の逆）：∫ u dv = u v − ∫ v du。
  • 部分分数分解、三角置換、数値積分（台形則、シンプソン法など）も重要です。

その他の概念

  • 不定積分は原始関数の全体を表し、定積分は実際の数値（面積や体積などの量）を返します。
  • 広義積分（無限区間や特異点がある場合）は収束性の判定が必要です（畳み込み、比較判定など）。
  • 多重積分（重積分）は二次元・三次元の領域での体積や質量の計算に用いられ、順序の交換や極座標・球座標などの座標変換が役立ちます。

まとめ（実用上の注意）

積分は「小さな寄与を総和して全体を得る」ための基本的な道具であり、微分とは逆向きの操作です。記号 ∫ は和（summa）を表す由来があり、リーマン和を通じて厳密に定義されます。面積・体積・距離・仕事・確率など、多くの応用分野で不可欠な概念です。計算には基本的な原始関数の知識に加え、置換や部分積分などのテクニック、場合によっては数値的手法が必要になります。

Zoom

積分とは、a, b, y = f(x)が与えられたとき、曲面sを求めることです。上図のaからbへの積分の公式は次のようになります。
    式は   ∫ a b f ( x ) d x {\displaystyle \int limits _{a}^{b}f(x)dx} {\displaystyle \int \limits _{a}^{b}f(x)\,dx}

インテグラル（動画）とはZoom
インテグラル（動画）とは

統合の方法

アンチダービティブ

微積分の基本定理では、積分は反微分である。

関数２ x {displaystyle 2x}を取ると{\displaystyle 2x}例えば、2 x {\displaystyle 2x}の積分が x 2 {\displaystyle x^{2}}{\displaystyle 2x}であると言うことができる。{\displaystyle x^{2}}.積分ではなく積分と言うのは、関数の反微分は一意ではないからである。例えば、x 2 + 17 {\displaystyle x^{2}+17{\displaystyle x^{2}+17}} は、2 x {\displaystyle 2x}{\displaystyle 2x} にも微分する。このため、反微分をとるときには、定数Cを加えなければならない。これを不定積分と呼ぶ。これは、関数の微分を求めるとき、定数が0になるからである。

f ( x ) = 5 x 2 + 9 x + 15 {displaystyle f(x)=5x^{2}+9x+15,} .{\displaystyle f(x)=5x^{2}+9x+15\,}

f ′ ( x ) = 10 x + 9 + 0{\displaystyle f'(x)=10x+9+0\,}{displaystyle f'(x)=10x+9+0,} .0に注意：微分だけでは見つけられないので、積分は

∫ ( 10 x + 9 ) d x = 5 x 2 + 9 x + C{\displaystyle \int (10x+9)\,dx=5x^{2}+9x+C} {\displaystyle

シンプルな方程式

y = x 2 {\displaystyle y=x^{2}}の{\displaystyle y=x^{2}}ような単純な方程式は、次の技法を使って、xに関して積分することができる。積分するには、xが上げられた乗に1を加えて、xをこの新しい乗の値で割る。したがって、正規方程式の積分は次のようになる。 ∫ x n d x = x n + 1 n + 1 + C {\displaystyle \int _{,}^{,}x^{n}dx={frac {x^{n+1}}{n+1}+C}}。 {\displaystyle \int _{\,}^{\,}x^{n}dx={\frac {x^{n+1}}{n+1}}+C}

最後のd x {\displaystyle dx}{\displaystyle dx}は、xに対して積分していること、つまりxが変化すると積分していることを示している。これは微分の逆であることがわかる。しかし、積分するときには定数Cというものが加わります。これは積分の定数と呼ばれています。これは，整数を微分するとゼロになるので，ゼロを積分するとCという整数が得られるからです．

複数の項を持つ方程式は、個々の項を統合することで単純に統合されます。

∫ x 2 + 3 x - 2 d x = ∫ x 2 d x + ∫ 3 x d x - ∫ 2 d x = x 3 3 + 3 x 2 - 2 x + C {displaystyle int _{\,}^{.♪x^{2}+3x-2dx=int _\{\,}^{\,}x^{2}dx+\int _{3xdx-\int _{\,}^{3xdx={\frac {x^{3}}{3}}+{\frac {3x^{2}}{2}-2x+C}. {\displaystyle \int _{\,}^{\,}x^{2}+3x-2dx=\int _{\,}^{\,}x^{2}dx+\int _{\,}^{\,}3xdx-\int _{\,}^{\,}2dx={\frac {x^{3}}{3}}+{\frac {3x^{2}}{2}}-2x+C}

e と ln を含む統合

eと自然対数を使った積分には、ある規則がある。最も重要なことは、e x {displaystyle e^{x}}{\displaystyle e^{x}}は、それ自体の積分（積分の定数を加えたもの）であることである： ∫ e x d x = e x + C {\displaystyle int _{,}^{,}e^{,}e^{x}dx=e^{x}+C} {\displaystyle \int _{\,}^{\,}e^{x}dx=e^{x}+C}

自然対数lnは、1 / x {\displaystyle 1/x{\displaystyle 1/x}} を持つ方程式を積分するときに便利である。これらは、上の式（乗に１を足して、乗で割る）では積分できない。その代わり、１／ｘの積分はln x {\displaystyle 1/x}{\displaystyle 1/x}だ{\displaystyle \ln x}。 {\displaystyle \int _{\,}^{\,}{\frac {1}{x}}dx=\ln x+C}

もっと一般的な形で∫ f ′ ( x ) f ( x ) d x = ln | f ( x ) | + C {\displaystyle \int _{\,}^{\,}{\frac {f'(x)}{f(x)}}}dx=ln {|f(x)|}+C} {\displaystyle \int _{\,}^{\,}{\frac {f'(x)}{f(x)}}dx=\ln {|f(x)|}+C}

2本の縦棒は絶対値を示し、f ( x ) {\displaystyle f(x)}f(x)の符号（正負）は無視される。これは、負の数の自然対数には値がないからである。

物件情報

関数の和

関数の和の積分とは、各関数の積分の和である。

∫ a b [ f ( x ) + g ( x ) ] d x = ∫ a b f ( x ) d x + ∫ a b g ( x ) d x {\displaystyle int \limits _{a}^{b}[f(x)+g(x)]d x=int \limits _{a}^{b}f(x)Dx+\,dx+int limits _{a}^{b}g(x)Dx} .{\displaystyle \int \limits _{a}^{b}[f(x)+g(x)]\,dx=\int \limits _{a}^{b}f(x)\,dx+\int \limits _{a}^{b}g(x)\,dx}

その証明は簡単です。積分の定義は和の極限である。したがって

∫ a b [ f ( x ) + g ( x ) ] d x = lim n → ∞ ∑ i = 1 n ( f ( x i ∗ ) + g ( x i ∗ ) )♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ {\displaystyle \int \limits _{a}^{b}[f(x)+g(x)]\,dx=\lim _{n\to \infty }\sum _{i=1}^{n}\left(f(x_{i}^{*})+g(x_{i}^{*})\right)}

∑ i = 1 n f ( x i ∗ ) + ∑ i = 1 n g ( x i ∗ ) { } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } } {\displaystyle =\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})+\sum _{i=1}^{n}g(x_{i}^{*})}

= ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ {\displaystyle =\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})+\lim _{n\to \infty }\sum _{i=1}^{n}g(x_{i}^{*})}

∫a b f ( x ) d x + ∫a b g ( x ) d x {\displaystyle =int limits _{a}^{b}f(x)Dx+\,dx+int ¶int ¶limits _{a}^{b}g(x)Dx} {\displaystyle =int ﾘﾐｯﾂ _{a}^{b}f(x)Dx {\displaystyle =\int \limits _{a}^{b}f(x)\,dx+\int \limits _{a}^{b}g(x)\,dx}

どちらの積分も同じ限界を持っていることに注意してください。

統合における定数

定数が関数を伴った積分の中にあるとき、その定数を取り出すことができる。さらに、定数cが関数を伴わない場合、その値はc * xとなります。

∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x {\displaystyle int ﾘﾐｯﾂ _{a}^{b}cf(x)

これは定数でしかできません。

∫ a b b c c d x = c ( b - a ) {\displaystyle {\displaystyle \int \limits _{a}^{b}c\,dx=c(b-a)}

証明は再び積分の定義によるものです。

その他

a, b, c が順番に（すなわち、x軸上で互いに後から）並んでいる場合、点aから点bへのf(x)の積分と点bから点cへのf(x)の積分は、点aから点cへの積分に等しくなります。

∫a b f ( x ) d x + ∫b c f ( x ) d x = ∫a c f ( x ) d x {displaystyle int \ limits _{a}^{b}f(x)x+int \,dx=int limits _{b}^{c}f(x)x=int limits _{a}^{c}f(x)x}{\displaystyle \int \limits _{a}^{b}f(x)\,dx+\int \limits _{b}^{c}f(x)\,dx=\int \limits _{a}^{c}f(x)\,dx} if they are in order.(これは、a,b,cが順番でない時も、∫a b f ( x ) d x = - ∫b a f ( x ) d x {\displaystyle int \limits _{a}^{b}f(x)x,dx{\displaystyle \int \limits _{a}^{b}f(x)\,dx=-\int \limits _{b}^{a}f(x)\,dx}=int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡int ➡tt

∫ a a f ( x ) d x = 0 {displaystyle \int ﾘﾐｯﾂ _{a}^{a}f(x){\displaystyle \int \limits _{a}^{a}f(x)\,dx=0}これは微積分の基本定理(FTC)に従う。F(a)-F(a)=0

∫ a b f ( x ) d x = - ∫ b a f ( x ) d x {\displaystyle ➡︎ ➡︎ ➡︎ ➡︎ ➡︎ ➡︎ ➡︎ ➡︎ ➡︎ ➡︎ ➡︎ ➡︎ ➡︎{\displaystyle \int \limits _{a}^{b}f(x)\,dx=-\int \limits _{b}^{a}f(x)\,dx}またしてもFTCに倣ってF (b ) - F (a ) = - [ F (a ) - F (b ) ] {\displaystyle F(b) -F(a)=-[F(a) -F(b) ]} } {\displaystyle F(b)-F(a)=-[F(a)-F(b)]}

質問と回答

Q:積分とは何ですか?


A:積分とは方程式のグラフの下にある空間のことで，「曲線の下の領域」とも呼ばれます．微分の逆で，微積分と呼ばれる数学の一分野です．

Q:積分の記号はどのようなものですか?


A:微積分の積分は∫{displaystyle ↵{int _{,}^{,}}というS字のような形をしています。

Q: 積分と微分はどのように関係しているのですか?


A: 積分と導関数は微積分の基本定理で結ばれており，積分は導関数で反転することができます．

Q: 積分はどのようなときに使うのですか?


A:積分は，問題に単位を乗じるときや，立体の体積を求めるときに使うことができます．二次元のものを幅が出るまで足し合わせて、三次元とその体積を求めるのに役立ちます。

Q: 積分は和算とどう違うのですか?


A:積分は，たくさんの小さなものを足し合わせるという点では和と似ているが，積分の場合は，その間にあるすべての小数や分数も足し合わせなければならない．

Q: リーマン和とは何ですか?


A:リーマン和とは、レートグラフの小さなスライスを足し合わせて、1つの全体方程式を構成することです。


百科事典を検索する
AlegsaOnline.com - 2020 / 2025 - License CC3