ノモグラム
ノモグラムやアライメント・チャート、アバクは、計算のためのグラフです。数学的関数の計算結果を示す2次元の図です。
ノモグラフィーという分野は、1884年にフランスのエンジニア、フィルバート・モーリス・ドカーニュ（1862-1938）によって発明された。ノモグラフィーは、複雑な数式をグラフィカルに素早く計算するために、長年にわたってエンジニアに利用されてきました。ノモグラフは、標準的なデカルト座標ではなく、ドカニュが発明した平行座標系を使用しています。
ノモグラムは、方程式の各変数に対応するn個の目盛りで構成されています。n-1個の変数の値を知ることで、未知の変数の値を求めたり、ある変数の値を固定することで、固定されていない変数間の関係を調べたりすることができます。
結果は、スケール上の既知の値に直定規を敷き、その変数のスケールを横切るところから未知の値を読み取ることで得られる。直定規によって作られた仮想的な線または描かれた線は、指標線またはアイソプレットと呼ばれます。
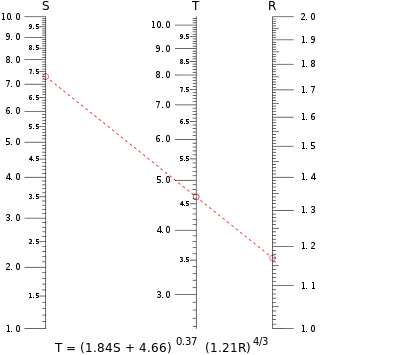
典型的なパラレルスケールのノモグラム。この例では、S=7.30とR=1.17を方程式に代入して、Tの値を計算しています。等値線は4.65弱でTの目盛りを越えています。
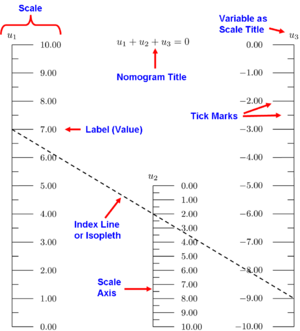
パラレルスケール・ノモグラムの構成要素
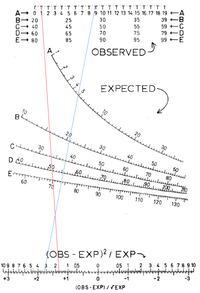
カイ二乗分布ノモグラム
使用
ノモグラムは約75年前から広く使われていました。ノモグラムは、ポケット電卓の時代になる前に、迅速で正確な計算を可能にしました。ノモグラムの結果は、1本または複数の線を引くことで素早く確実に得られます。代数方程式を解いたり、表でデータを調べたり、計算尺を使ったり、方程式に数字を代入したりする必要はありません。また、ノモグラムが表す基礎方程式を知る必要もありません。
ノモグラムのデザインには、その分野の知識が盛り込まれています。例えば、より精度の高い大きなノモグラムを作成するために、ノモグラファーは通常、合理的で問題に関心のあるスケール範囲のみを含めます。また、多くのノモグラムには、参照ラベルや色のついた領域など、その他の有用なマークが含まれています。これらはすべて、ユーザーにとって有用な道しるべとなります。
ノモグラムは計算尺と同様、グラフィカルなアナログ計算機である。計算尺は汎用的な計算機ですが、ノモグラムは特定の計算を行うために設計されています。計算尺は一般的な計算機ですが、ノモグラムは特定の計算を行うために設計されています。
質問と回答
Q: ノモグラムとは何ですか?
A:ノモグラムとは、数学的関数の計算を与える、計算に用いるグラフのことです。
Q:ノモグラフィーという分野を発明したのは誰ですか?
A:ノモグラフィーという分野は、1884年にフランスのエンジニア、フィルバート・モーリス・ドカーニュによって発明されました。
Q:ノモグラムはどのような目的で使われたのですか?
A: ノモグラムは、技術者が複雑な数式を素早く図式化するために、長年使用されてきました。
Q: ノモグラムはいくつの目盛りで構成されていますか?
A: ノモグラムは、方程式の各変数に対して1つずつ、n個のスケールのセットで構成されています。
Q: ノモグラムを使って、未知の変数の値をどのように求めることができますか?
A: n-1個の変数の値を知っている場合、未知の変数の値は、スケール上の既知の値に直定規を置き、その変数のスケールと交差するところから未知の値を読み取ることによって見つけることができます。
Q: 直定規が作る仮想の線、または描かれた線は何と呼ばれていますか?
A:直定規によって作られる仮想的な線、または描かれた線は、指標線または等倍線と呼ばれます。
Q:ノモグラムではどのような座標系が使われるのですか?
A: ノモグラムでは、標準的なデカルト座標ではなく、ドカーニュが考案した平行座標系を使用しています。
