計算尺(スライドルール)とは|歴史・仕組み・種類・使い方を解説
計算尺(スライドルール)の歴史・仕組み・種類・使い方を図解でわかりやすく解説。原理や実例、選び方まで初心者にも役立つ完全ガイド。
スライドルール、またはスリップスティックは、機械的なアナログコンピュータである。スライドルールは、主に乗算や除算に使用され、また、根、対数、三角法などの「科学的な」機能のために使用されますが、通常は足し算や引き算のためではありません。
スライドルールの多くの異なるスタイルがあります。彼らは通常、線形または円形です。彼らは、マーキング(スケールと呼ばれる)の標準化されたセットを持っています。これらのスケールは、数学的計算のために使用されます。いくつかのスライドルールは、航空や金融のように、特別な使用のために作られています。これらのスライド規則には、通常のスケールと同様に、それらのアプリケーションのための特別なスケールがあります。
ウィリアム・オフトレッドらは、1600年代にスライドルールを開発した。スライドルールは、ジョン・ネイピアによる対数に関する作業に基づいています。電子計算機が開発される前は、スライドルールは、科学や工学で最も頻繁に使用されるツールでした。スライドルールの使用は、デジタルコンピューティングデバイスが徐々に導入されたとしても、1950年代と1960年代を介して成長し続けた;しかし、1974年頃ポケット電卓は、スライドルールは主に時代遅れにし、ほとんどのサプライヤーは、ビジネスを去った。
簡単な仕組み(原理)
スライドルールは、対数の性質(log(AB) = log A + log B)を利用して、乗算や除算を線形の並べ替えで行います。ルール本体(固定部分)と中央の可動スライド(スライド)を相対的にずらし、目盛りどうしを合わせることで演算を行います。さらに、透明のカーソル(移動目盛り)を使って、正確な位置を読み取ります。
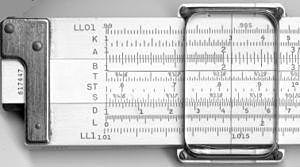
代表的なスケール(目盛り)
- C/D:乗除算の基本となる対数目盛り。
- A/B:C/Dの2乗(2乗根・2乗の計算に使用)。
- K:3乗や3乗根に用いられる目盛り。
- L:常用対数の線形目盛り(小数部の扱いに便利)。
- S/T/ST:三角関数用の目盛り(sin, tan, 小角用のSTなど)。
主要な種類
- 線形型(直線型):最も一般的で、片手で扱いやすい。一般の理工系で広く使われた。
- 円形:端がないため有効桁数を増やせる設計のものもあり、長さを短くしつつ広い目盛りを得られる。
- 二重面(デュプレックス):両面に目盛りがあるタイプで、多機能かつ読み取りやすい。
- 円筒形(シリンドリカル):非常に長い目盛りを巻き付けることで高精度を可能にする高級モデル。
- 特殊用途モデル:航空用、金融用、土木や電気用など、特定の計算に特化した専用スケールを備える。
基本的な使い方(例)
乗算(例:2 × 3)
- 下側のDスケール上で「2」の位置を見つける。
- 上側のCスケールの「1」(インデックス)をその「2」の位置に合わせる。
- Cスケール上の「3」の下に来るDスケールの値を読むと「6」に近い値が得られる(小数点の位置は自分で判断)。
除算はこの逆の操作(被除数の位置に除数の目盛りを合わせ、Cの1の位置にある値を読む)で行います。
平方根・三角関数の計算
平方・平方根はA/BとC/Dの関係で求められます。例えばD上の数の平方根は対応するA目盛りを使って読むことができます。三角関数はS,T,STなどの目盛りで読み取り、角度を対応する位置に合わせて正弦・正接などの値を求めます。
精度と桁合わせ(有効数字の扱い)
スライドルールは一般に2〜3桁の有効数字で素早く概算を得るのに適しています。目盛り自体は細かいが、実用上は桁合わせ(小数点位置の推定)を自分で行う必要があり、前後の概算や単位の知識で桁を判断します。このため、工程設計や概算計算、検算に向いています。
手入れと保管
- 直射日光や高温多湿を避け、変形や目盛りの劣化を防ぐ。
- 滑りが悪くなったら専用の滑剤や薄めた中性洗剤で汚れを落とし、乾燥させてから軽く潤滑する(過剰な油は目盛りに悪影響)。
- カーソルの透明部はアルコールでやさしく拭くと視認性が回復する。
歴史的背景と衰退
スライドルールの原理は、ジョン・ネイピアの対数に由来し、ウィリアム・オフトレッドらが17世紀に実用的な形に発展させました。その後、19世紀から20世紀半ばにかけて、理工系や航空、建設、金融など幅広い分野で標準的な計算道具として使われました。
しかし電子式計算機、特にポケット電卓が一般化した1970年代以降は次第に姿を消しました。現在は教育目的や収集、趣味の対象、あるいは電子機器に依存しない概算ツールとして残っています。また、スライドルールの原理を学ぶことは対数や桁合わせの感覚を養うのに有効です。
参考:代表的なメーカーと収集
歴史的にはKeuffel & Esser(K&E)、Pickett、Faber-Castell、Hemmiなどのメーカーが知られています。ヴィンテージのスライドルールはコレクターズアイテムとしても人気があり、目盛りの種類や材質(木製、セルロイド、金属製など)で価値が変わります。
スライドルールは現代の電子ツールほどの利便性はないものの、原理が直感的で学びやすく、計算の「道具としての考え方」を理解するのに非常に有用な歴史的・教育的資産です。

2の倍数になるように配置されたスライドルールで、D(下)の目盛りの数字は、C(中)の目盛りの上の数字の2倍になります。

代表的な10インチ学生用スライドルール(ピケットN902-Tシンプレックストライグ
基本的な考え方
その最も基本的な形では、スライドルールは、数字の急速な乗算と除算を可能にするために2つの対数スケールを使用しています。これらの一般的な操作は、紙の上で行うと時間がかかり、エラーが発生しやすくなります。より複雑なスライドルールでは、平方根、指数、対数、三角関数などの他の計算が可能です。
数学的な計算は、スライドする中央ストリップ上のマークを固定ストリップの1つに合わせることによって行われます。その後、他のマークの相対的な位置を観察することができます。マークに合わせた数字は、積、商、またはその他の計算結果の近似値を与えます。
ユーザーは、精神的な推定に基づいて、結果の小数点の位置を決定します。より正式な計算では、小数点を追跡するために科学的記法が使用されます。計算における足し算と引き算のステップは、スライドルールではなく、一般的に精神的に、または紙の上で行われます。
ほとんどのスライドルールは、同じ長さの3本の直線状のストリップを備えています。これらのストリップは平行に配置され、中央のストリップが他の2つのストリップに対して長さ方向に相対的に移動できるように連動しています。外側の2本のストリップは、その相対的な位置が変わらないように固定されています。
いくつかのスライド規則(「二重」モデル)では、規則とスライドストリップの両側に目盛りがあり、外側のストリップの片側とスライドストリップの両側にあるものもあれば、片側のみにあるものもあります(「単純」規則)。垂直整列線を持つスライドカーソルは、互いに隣接していない、または二重モデルではルールの反対側にある目盛り上の対応する点を見つけるために使用されます。カーソルは、任意のスケールの中間結果を記録することもできます。

スライドルールのカーソル
スライドルールを使って計算する
乗算
対数は、掛け算と割り算を足し算と引き算に変換する log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} 









たとえば、上の図では、スライドルールが上の目盛りの7を下の目盛りのどの数字よりも上に配置していないので、2×7の答えが出ないことを示しています。このような場合、ユーザは、下の図のように、右のインデックスが2に揃うまで上のスケールを左にスライドさせて、効果的に2ではなく0.2を乗算することができます。
![]()
ここで、スライドルールの使用者は、最終的な答えを修正するために、小数点を適切に調整することを忘れてはなりません。2×7を求めたかったのですが、代わりに0.2×7=1.4を計算しました。つまり、本当の答えは1.4ではなく14です。スライドをリセットすることは、2×7のようなスケール外の結果になる乗算を処理する唯一の方法ではなく、他のいくつかの方法があります。
- (1) ダブルディケイドスケールのAとBを使用します。
- (2)折りたたまれた目盛りを使います。この例では、Cの左1をDの左2と反対にして、CFの7にカーソルを合わせ、DFから結果を読み取る。
- (3) CI反転スケールを使用します。CIスケールの7をDスケールの2の上に置き、DスケールからCIスケールの1の下にあるDスケールの結果を読み取る。1はCIスケール上の2箇所にあるので、そのうちの1箇所は常にオンスケールになります。
- (4) CIの反転スケールとCスケールの両方を使う。CIの2とDの1を並べて、Dの結果をCスケールの7の下に読み取る。
方法1は理解しやすいですが、精度の低下を伴います。方法3には、2つのスケールしかないという利点があります。
事業部
下の図は、5.5/2の計算を示しています。 上の目盛りの2は下の目盛りの5.5の上にあります。上の目盛りの1は商の2.75の上にあります。除算を行う方法は1つだけではありませんが、ここで紹介する方法には、最終的な結果がスケールを外れることがないという利点があります。

その他の事業
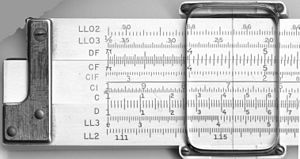
対数スケールに加えて、いくつかのスライドルールには、他の補助スケールにエンコードされた他の数学関数があります。最も人気があったのは、三角法、通常はサインとタンジェント、共通対数(log10) (乗数スケールで値の対数を取るため)、自然対数(ln)と指数(ex)スケールでした。いくつかの規則には、三角形の辺を表すピタゴラススケールや、円を表すスケールがあります。その他にも、双曲関数を計算するためのスケールを特徴とするものもあります。線形規則では、スケールとそのラベル付けは高度に標準化されており、通常はどのスケールがどの順番で含まれているかという点でのみ変化が生じます。
| A,B | にじょうけい |
| C, D | 単十年対数目盛 |
| K | さんじゅうすう |
| CF、DF | 単一からではなくπから始まるCとDのスケールの"折りたたまれた"バージョン; これらは2つの場合に便利です。第一に、ユーザが積が10に近いと推測しても、それが10より少し小さいのか、少し多いのかわからない場合、折りたたまれた目盛りは、目盛りから外れる可能性を避けます。第二に、始点を10の平方根ではなくπにすることで、(科学や工学の公式によくあるように)πを掛けたり割ったりすることが簡単になります。 |
| CI、DI、DIF | "倒立目盛り |
| S | Dスケールの正弦・余弦を求めるのに使用されます。 |
| T | DスケールとDIスケールの接線とコタンジェントを見つけるために使用されます。 |
| ST、SRT | 小角の正弦や接線、度ラジアン変換に使用されます。 |
| L | 線形目盛 |
| LLn | 対数対数目盛 |
| Ln | 線形スケールで、自然な(基底e)対数とe x {\displaystyle e^{x}}を見つけるために、CとDスケールと共に使用される。 |
| ||
| K&E 4081-3スライドルールの表裏の目盛り。 |
1931年にギルソン社が製造したバイナリスライドルールは、分数に限定した足し算・引き算機能を行っていました。
ルーツとパワー
尺度には、10進数(CとD)、20進数(AとB)、30進数(K)がある。x 2 {displaystyle x^{2}}を計算するには
x y {displaystyle x^{y}}

三角法
S、T、ST スケールは、三角関数や三角関数の倍数、角度の度数などに使用されます。多くのスライド規則では、S、T、STの目盛りには度と分が表示されています。いわゆるデシトリグモデルでは、代わりに度数の10進数を使用します。
対数と指数
基数10の対数や指数は、線形であるLスケールを使って求めます。スライドルールの中には、基底eのためのLnスケールがあるものもあります。
Lnスケールは、11年生の学生、スティーブンB.コーエン、1958年に発明されました。当初の目的は、ユーザーがLnスケールで指数x(0から2.3の範囲)を選択し、C(またはD)スケールでexを、CI(またはDI)スケールでe-xを読むことができるようにすることでした。Pickett, Inc.は、このスケールの独占的権利を与えられた。その後、本発明者は2.3の限界を超えて範囲を拡張するためにLnスケール上に一連の「マーク」を作成しましたが、ピケットはそのスライドルールのいずれかにこれらのマークを組み込むことはありませんでした。[]
加減算
スライドルールは一般的に足し算と引き算には使用されませんが、それにもかかわらず、2つの異なるテクニックを使用して足し算と引き算を行うことができます。
CとD(またはそれに匹敵するスケール)で足し算と引き算を実行する最初の方法は,問題を除算の1つに変換する必要があります.足し算では,2つの変数の商に除数の1倍を加えたものが,それらの和に等しくなります.
x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}+1right}y}}。
減算については、2つの変数の商から除数の1倍を引いたものが、その差に等しい。
x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}-1right)y}}。
この方法は、グラビティパイプ(GRAPE)スーパーコンピュータや隠れマルコフモデルなどの特殊なコンピュータアプリケーションで、対数系の高速電子回路に用いられている加算・減算手法に似ています。
2 番目の方法は、一部のモデルで利用可能なスライディングリニア L スケールを使用します。加算と減算は、カーソルを左(減算の場合)または右(加算の場合)にスライドさせ、スライドを0に戻して結果を読み取ることで行われます。
物理設計
標準的な線形規則
スライドルールの長さは、スケールの公称長さで引用されています。最も一般的な"10インチ"モデルのスケールは、いくつかのルールは、結果があふれたときに操作を簡素化するためにわずかに拡張スケールを提供していますが、彼らはメトリック規格に作られたように、実際には長さが25 cmです。ポケットルールは通常5インチです。数メートルの長さのモデルは、教育目的のために教室で吊るされるように販売された.[1]
一般的に、分割は2つの有効数字の精度にスケールをマークし、ユーザーは3つ目の数字を推定します。一部のハイエンドのスライドルールには、マーキングを見やすくする拡大カーソルが付いています。このようなカーソルは、10インチのスライドルールが20インチと同様に機能することを可能にし、効果的に測定値の精度を2倍にすることができます。
他にも様々な便利な機能が開発されています。三角スケールは、いわゆる「ダルムシュタット」スタイルで、黒と赤の二重ラベルが付けられていることがあります。二重スライド規則は、しばしば裏面の目盛りの一部を複製しています。目盛りは、より高い精度を得るために「分割」されることが多いです。
特殊なスライドルールは、工学、ビジネス、銀行業務のさまざまな形態のために発明されました。これらは多くの場合、一般的な計算を直接特殊な尺度で表現したもので、例えばローンの計算、最適な購入量、または特定のエンジニアリング方程式などがありました。たとえば、フィッシャーコントロールズ社は、工業用流量制御弁の適切なサイズを選択するために使用される方程式を解くために適応したカスタマイズされたスライドルールを配布した。[]
円形スライドのルール
円形のスライドルールには、2つのカーソル(左)と1つの可動ディスクと1つのカーソル(右)の2つの基本的なタイプがあります。デュアルカーソルバージョンは、ダイヤルの周りに回転しているカーソル間の固定角度を維持することにより、乗算と除算を実行します。シングルカーソルバージョンは、スケールの適切な位置合わせにより、標準のスライドルールに似た動作をします。
円形スライドルールの基本的な利点は、ツールの最長寸法が約3のファクター(すなわちπ)で縮小されたことです。たとえば、10cmの円形の外側のスケールは、30cmの通常のスライドルールと同等の最大精度を持つことになります。円形のスライドルールはまた、スケールが"回り込む"ように設計されていたので、"スケール外"の計算を排除します; 彼らは、結果が1.0に近いときに再方向を変更する必要はありません-ルールは常にスケール上にあります。しかし、S, T, LLのような非循環的な非スパイラルスケールの場合は、スケールの長さを短くして端の余白のためのスペースを確保します。
円形のスライドルールは、機械的にはより頑丈で滑らかな動きをしますが、スケールのアライメント精度は中央のピボットのセンタリングに影響を受けます。ピボットの中心から0.1mmの微小なずれは、0.2mmの最悪の場合のアライメントエラーをもたらします。しかし、ピボットはフェースとカーソルの傷を防ぎます。最高精度のスケールは、外側のリングに配置されています。スプリット」スケールではなく、ハイエンドのサーキュラールールでは、ログオブログスケールのようなより複雑な操作にスパイラルスケールを使用しています。8インチのプレミアムサーキュラールールには、50インチのスパイラル・ログ・ログ・スケールが付いていました。
円形スライドルールの主な欠点は、回転する円盤に沿って図形を配置することの難しさ、およびスケールの数が限られていることです。また、円形スライドルールのもう一つの欠点は、重要度の低い目盛りは中心に近く、精度が低いことです。ほとんどの生徒はリニアスライドルールでスライドルールを学びましたが、スライドルールを切り替える理由を見つけることはできませんでした。
世界中で日常的に使われているスライドルールの一つにE6Bがあります。これは、1930年代に飛行機のパイロットのために最初に作成された円形のスライドルールであり、デッドレコニングに役立ちます。フレームに印刷された目盛りの助けを借りて、それはまた、時間、距離、速度、温度値、コンパスの誤差、燃料使用量の計算を変換するような雑多なタスクに役立ちます。いわゆる「祈りの車輪」と呼ばれるものは、今でもフライトショップで販売されており、広く使われています。GPSの登場で空中航法のデッドレコニングが減少し、携帯電卓がその機能の多くを引き継いでいますが、E6Bはプライマリまたはバックアップデバイスとして広く使用されており、大多数のフライトスクールでは学生にある程度の習得を求めています。
1952 年、スイスの時計メーカーであるブライトリングは、飛行計算に特化したサーキュラ ル・スライド・ルールを内蔵したパイロット用腕時計「ナビタイマー」を発表しました。ナビタイマーは、ブライトリングが「ナビゲーション・コンピューター」と呼んでいたもので、対気速度、上昇/下降速度、飛行時間、距離、燃料消費量の機能に加えて、キロ・海里、ガロン・リットルの燃料量換算機能を備えていました。
材料
伝統的にスライドルールは、マホガニーやツゲなどの硬い木で作られ、ガラスや金属のカーソルが付いていました。少なくとも1つの高精度な楽器はスチール製でした。
1895年、日本の会社であるHemmi社は、寸法が安定していて丈夫で、自然に自己潤滑性があるという利点を持つ竹からスライドルールの製造を開始しました。これらの竹製スライドルールは1933年9月にスウェーデンで導入されました[2]。スケールは、セルロイドまたはプラスチックで作られていました。後のスライド規則はプラスチック製、またはプラスチックで塗装されたアルミニウム製であった。後のカーソルはテフロンベアリング上を滑るアクリルまたはポリカーボネートであった。
すべてのプレミアムスライドルールは、数字や目盛りが刻印されていて、その後、塗料や他の樹脂で満たされていました。マーキングが摩耗する可能性があるため、塗装や刻印スライドルールは劣っていると見られていた。それにもかかわらず、ピケット、おそらくアメリカで最も成功したスライドルールの会社は、すべての印刷されたスケールを作った。プレミアムスライドルールには、ルールが不慮の事故でバラバラにならないように巧妙なキャッチと、タブレットの上でこすれないようにスケールとカーソルを保護するためのバンパーが含まれていました。刻印のお手入れ方法は、スチールウールで軽くこするのがおすすめです。塗装されたスライドルールや気の弱い方には、市販のウィンドウクリーニング液を薄めたものと柔らかい布を使用してください。

ブライトリング ナビタイマー サーキュラースライドルール付き腕時計

逆目盛、平方目盛、立方目盛のみのシンプルな円形スライドルール(株式会社コンサイス製、東京都)。裏面には38のメートル/インペリアル変換係数の便利なリストが付いています。

Pickett円形スライドルール、2つのカーソル付き。(直径10.9cm) 裏面には目盛りとカーソルが1つ付いています。
歴史
スライドルールは、ジョン・ネイピアが対数の概念を発表した直後の1620年から1630年頃に発明されました。オックスフォードのエドマンド・ガンターは、追加の測定ツールを使用して、乗算や割り算に使用できる単一の対数目盛を持つ計算装置を開発しました。このスケールの最初の記述は、イギリスの数学者エドマンド・ウィンゲイト(Edmund Wingate, c. 1593 - 1656)が1624年にパリで発表した「L'usage de la reigle de proportion en l'arithmetique & geometrie」という本の中で発表したものです。この本には、片面が対数目盛、もう片面が表計算目盛の二重目盛が記載されている。1630年にはケンブリッジのウィリアム・オフトレッドが円形のスライドルールを発明し、1632年には手で持った2つのグンタールールを組み合わせて、現代のスライドルールと認識できる装置を作りました。ケンブリッジの同世代のアイザック・ニュートンと同様に、オトレッドは自分のアイデアを学生に個人的に教えていましたが、それを公開するのが遅れ、ニュートンと同様に、彼はかつての学生であるリチャード・デラメインとウィンゲートの先行主張をめぐって、優先順位をめぐる激しい論争に巻き込まれました。オフトレッドの考えが公開されたのは、1632年と1653年に弟子のウィリアム・フォースターの出版物の中でのみであった。
1677年、ヘンリー・コッゲシャルは、コッゲシャル・スライド・ルールと呼ばれる木材測定のための2フィートの折りたたみ式ルールを作成しました。ツールのための彼の設計と使用は、数学的な照会の外にスライドルールの目的を与えた。
1722年には、ワーナーが2音階と3音階を導入し、1755年にはエヴェラールが倒立音階を導入しました。
1815年、ピーター・ロジェは対数を表示する目盛りを含む対数スライドルールを発明しました。これにより、根や指数を含む計算を直接行うことができるようになりました。これは、特に分数乗の計算に便利でした。
モダンなフォルム
より近代的な形は、1859年にフランスの砲兵中尉アメデ・マンハイムによって考案されました。エンジニアリングが専門的な活動として認められるようになったのはその頃で、スライドルールはヨーロッパで広く使われるようになりました。1881年にエドウィン・ターチャーが円筒形のルールを米国に導入するまで、米国では一般的にはなりませんでした。二重のルールは1891年にウィリアム・コックスによって発明され、ニューヨークのKeuffel and Esser Co.によって製造されました。
天文作業にも細かい計算が必要で、19世紀のドイツでは、ある天文台で長さ2メートルほどのスチール製のスライドルールが使われていました。これには顕微鏡が取り付けられており、小数点以下6桁の精度が得られました。
第二次世界大戦では、迅速な計算を必要とする爆撃機や航海士は、しばしば特殊なスライドルールを使用していました。アメリカ海軍のある事務所では、特殊な計算のためにセルロイドカード(両面に印刷されている)を入れることができるアルミニウム製の本体とプラスチック製のカーソルを備えた汎用のスライドルール「シャーシ」を実際に設計しました。このプロセスは、航空機の航続距離、燃料使用量、高度を計算するために発明され、その後、他の多くの目的に適用されました。
1950年代と1960年代を通してスライドルールは、エンジニアの職業のシンボルであった(聴診器が医療職を象徴するのと同じ方法で)。ドイツのロケット科学者ヴェルナー・フォン・ブラウンは、彼がアメリカの宇宙計画で働くために第二次世界大戦後に米国に移動したときに、彼と一緒に2つの1930年代のヴィンテージネスラースライドルールを持ってきた[]ドイツのロケット科学者。彼は生涯を通じて、他のポケット計算機を使うことはありませんでした。スライドルールは、ロケットの設計パラメータやその他の数値を素早く見積もるために完璧に役立っていました。ピケットブランドのアルミニウム製スライドルールは、ピケットのN600スライドルールボックスの広告によると、月面を含む5回のアポロ宇宙ミッションで使用されました[3]。
工学部の学生やエンジニアの中には、10インチのスライドルールをベルトホルスターに入れて持ち歩いている人もいて、1970年代半ばになってもキャンパスではよく見かける光景でした。また、学生が自宅やオフィスで精密作業をするために10インチや20インチのスライドルールを持ち歩きながら、5インチのポケットスライドルールを持ち歩いていたこともありました。
2004年、教育研究者のDavid B. Sher氏とDean C. Nataro氏は、対数を先行させた高速計算のアルゴリズムであるprosthaphaeresisをベースにした新しいタイプのスライドルールを考案しました。しかし、最初のプロトタイプを超えたものを構築することへの実用的な関心はほとんどありませんでした。[4]
衰退
スライドルールの重要性は、1950年代には新しいが非常に乏しい資源である電子コンピュータが、1960年代に技術労働者に広く利用できるようになったので、減少し始めた。1957年にFortranが導入されたことで、中程度のサイズの数学的な問題を解くためのコンピュータが実用的になりました。IBMは、IBM 650 (1954年)、IBM 1620 (1959年)、IBM 1130 (1965年)の一連のより手頃なコンピュータを導入しました。John Kemeny の BASIC プログラミング言語 (1964年) は、学生が簡単にコンピュータを使用できるようにしました。1965年にはDEC PDP-8ミニコンピュータが発売されました。
コンピュータはまた、計算の性質を変えました。スライドルールでは、式を最も計算しやすい形にするために代数を扱うことに重点が置かれていました。スライドルールのユーザーは、計算を単純化するために、単純に近似したり、小さな項を削除したりしていました。Fortranを使うと、複雑な数式を教科書から入力しても、再構成の手間をかけずに済むようになりました。難しい問題に対して閉形式の解を見つけようとするよりも,数値積分の方が簡単であることが多かった.若いエンジニアが、スライドルールを数回スワイプするだけでできた問題を解くためにコンピュータの時間を要求することは、ユーモラスな決まり文句になりました。多くのコンピュータセンターでは、「緊急時にはガラスを割ってください」と書かれた額縁付きのスライドルールが壁に掛けられていました。
スライドルールを電子計算機に置き換えるためのもう一つのステップは、科学・工学用の電子計算機の開発でした。最初のものには、1965年に導入されたWang Laboratories LOCI-2があり、乗算と除算に対数を使用していました。HP-9100には、指数や対数に加えて三角関数(sin、cos、tan)が搭載されていました。三角関数をシフトと加算だけで計算できるCORDIC(座標回転デジタルコンピュータ)アルゴリズムを採用しています。この方法により、小型の科学計算機が開発されました。
スライドルールの最後の釘は、ポケットサイズの科学電卓の発売であり、1972年のヒューレット・パッカードHP-35がその最初のものであった。このような電卓は「スライドルール」電卓として知られるようになりました。数百ドルで、これでもほとんどの学生のための高価なものと考えられていた。プロのスライドルールもかなり高価になる可能性がありますが、ドラッグストアでは、しばしば20ドル以下のドルで基本的なプラスチック製のモデルを販売していました。しかし、1975年までには、基本的な4機能の電子計算機は50ドル以下で購入することができました。1976年までにTI-30は25ドル以下で科学計算機を提供していました。この時期以降、小型の科学電卓が手頃な価格になったため、スライドルールの市場は急速に枯渇した。

TI-30

スライドルールを使用しているエンジニア。背景に機械式計算機があることに注意してください。

ウィリアム・オフトレッド(1575-1660)、円形スライドルールの発明者
メリット
- スライドルールは、「誤った精度」と「有意性」の誤謬をほどほどにする傾向があります。スライドルールのユーザーが利用できる典型的な精度は、約3桁の精度です。これは、工学式への入力に利用可能なほとんどのデータと良好に対応しています。最新のポケット電卓を使用すると、精度は小数点以下7桁以上に表示されることがありますが、実際には結果は利用可能な入力データよりも高い精度になることはありません。
- スライドルールでは、結果の大きさの次数を継続的に推定する必要があります。スライドルールでは、1.5×30(これは45に等しい)は、1,500,000×0.03(これは45,000に等しい)と同じ結果が表示されます。コンピュータプログラムや電卓に不用意に数字を入力してしまうと、結果の妥当性が失われてしまう可能性があります。
- 同じ数の乗算や除算を連続して実行する場合、何も操作せずにスライドルールを見るだけで答えが決まることがよくあります。これは、テストの点数などのパーセンテージを計算するときや、キログラムあたりのドルなどの価格を比較するときに特に役立ちます。複数の速度-時間-距離の計算は、スライドルールを使えば、一目でハンズフリーで実行できます。
- スライドルールは電気に頼らない。
- スライドルールは、簡単に複製できる技術です。スライドルールの一例を挙げれば、非工業的なプロセスを用いて、初歩的な材料から、有能な職人によって、より多くのものを構築することができます。
- スライドルールは標準化が進んでいるので、別のルールに切り替えても何も学び直す必要はありません。
- スライドルールは汎用性が高く、人間のユーザーが手先の器用さが低下しているかもしれない状況や環境で操作することができます(例えば、保護手袋を必要とするため)。逆に、電卓はそのような状況では操作が難しい場合があります - スライドルールは、電卓の間違ったボタンを押すことで生じるエラーと同様の結果になることはほとんどありません。
- スライドルールは、ダンボールや紙で作ることができます。段ボールで作られた無料のチャートや特殊な計算機の多くは、実際には特殊な直線や円形のスライドルールです。
スライドルールと電子計算機を併用する利点の一つは、重要な計算を両方で行うことで確認できることです。
デメリット
- 機械的な不正確さからエラーが発生することがあります。
- スライドルールを使った計算は、アナログ入力とアナログ出力のため、精度が限られています。逆に、離散的な数値入力と浮動小数点電子演算のため、控えめな現代の電卓でも、少なくとも6桁の有効数字の出力分解能を持っています。
関連ページ
質問と回答
Q:計算尺とは何ですか?
A:計算尺とは、主に掛け算・割り算や、根・対数・三角などの科学的な関数に使われる機械式のアナログコンピュータのことです。
Q:計算尺にはどのような種類がありますか?
A:計算尺には直線と円形のものがあり、数学的な計算に使う目盛りが標準化されています。また、航空用や金融用に特別な目盛りをつけた特殊な計算尺もあります。
Q:誰が計算尺を発明したのですか?
A:計算尺は、ジョン・ネイピアの対数に関する研究に基づいて、ウィリアム・オルトレッドによって発明されました。
Q: 電子計算機はいつ開発されたのですか?
A: 電子計算機は1970年代以前にも開発されていましたが、1974年頃にポケット計算機が登場し、計算尺はほとんど使われなくなりました。
Q: 電子計算機が開発される前は、科学や工学の分野で何をよく使っていたのでしょうか?
A:電子計算機が開発される前は、理工系では計算尺がよく使われていました。
Q:デジタル計算機が登場した後、人々はいつまで計算尺を使い続けたのでしょうか?
A:デジタル計算機が徐々に普及し始めた1950年代から1960年代にかけて、計算尺は使われ続けました。
百科事典を検索する