抽象機械
オートマトン（automaton）とは、数学の概念の一つ。ステートマシンと呼ばれることもある。抽象的な機械のようなものである。
このような機械には、入力が与えられ、それを拒否するか、受け入れるかのどちらかです。自動販売機のようなものである。何かを買うときには、機械にコイン（またはお金）を入れる必要があります。そのコインが正しいものであれば、受け入れられ、要求されたアイテムは取り出せるように落とされます。もし、コインが間違っていれば、拒否されます。
内部的には、オートマトンはさまざまな状態を持っています。入力を与えると、その状態が変わることもあれば、変わらないこともあります。このように、オートマトンはすべての入力を通過して、一度に1つのアイテム（数学者はシンボルと呼ぶ）を消費します。シンボルがなくなったとき、オートマトンはある状態になります。これは最終的な状態かもしれません。この場合、入力は受け入れられます。そうでなければ、入力は拒否されます。
機械が数えられる有限の数の状態を持つ場合、それは有限状態機械と呼ばれる。このような機械のすべての状態と遷移を示した図を有限状態図という。
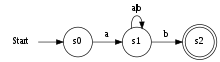
コンピュータサイエンスにおけるオートマトンの一般的な表現です。このオートマトンは、aで始まりbで終わる文字aとbのすべての配列を「受け入れる」。
問題点
現実の世界と同じように、複雑すぎて理解できない機械があります。そこで、数学者やコンピュータ科学者は、あるオートマトンが最小であるかどうかを自問します。もし最小でなければ、同じことができる、より少ない状態のオートマトンが存在するはずです。オートマトンの例として、チューリングマシンがあります。
質問と回答
Q:オートマトンとは何ですか?
A: オートマトンとは、数学の概念で、抽象的な機械のようなもので、入力が与えられると、それを拒否したり受け入れたりすることができます。
Q:オートマトンの別の呼び方は?
A:ステートマシンと呼ばれることもあります。
Q:オートマトンを自動販売機に例えることはできますか?
A:はい、自動販売機のように、コインやお金を入れて、そのコインが正しいものであれば、要求された商品を落として取り出せるようにするものです。
Q:オートマトンに入力されるとどうなるのですか?
A:オートマトンは、入力されたものを1つずつ消費しながら、内部でさまざまな状態になっています。オートマトンに入力を与えると、その状態が変化することもあれば、変化しないこともあります。
Q:オートマトンの記号がなくなったらどうするのですか?
A:記号がなくなると、オートマトンはある特定の状態になり、それが最終状態である可能性があります。この場合、入力は受け入れられ、そうでない場合は入力は拒否される。
Q: 有限状態機械とは何ですか?
A:機械が数えられる有限の数の状態を持つ場合、それは有限状態機械と呼ばれます。
Q:有限状態図とは何ですか?
A: そのようなマシンのすべての状態、および遷移を示す図を有限状態図といいます。
