数学とは何か:定義と主要分野(数・構造・空間・変化)と応用
数学とは何かを分かりやすく解説:数・構造・空間・変化の定義と主要分野、実生活や科学・工学での具体的応用例まで基礎から実践を網羅。
ギリシャ語の「μάθημα」(máthema)に由来する数学は、数、図形、パターンの研究を通して、抽象的な概念を定義し、論理的に結びつける学問です。語源的には「科学、知識、学習」を意味します。英語では単語 "mathematics" が使われ、短縮形としてアメリカ、カナダでは "math"、イギリス、オーストラリア、アイルランド、ニュージーランドでは "maths" と呼ばれることが多いです。学校や教育の場では、この用語はしばしば生徒向けに学校で学ぶ算数や幾何学、簡単な代数などに適用されます。
数学の主要な考え方と分野
- 数(数量): ものをどのように数え、量を表現し、計算するか。整数・有理数・実数・複素数などの体系、数えることが可能な対象とその性質を扱います。数論や算術、計算理論などが含まれます。
- 構造(代数): 対象がどのように組織化され、演算や関係によってどんな性質を持つかを研究します。集合、群、環、体、ベクトル空間などの抽象的構造を扱い、代数的な法則から一般的な定理を導きます(この考え方を示す語として構造や、どのように組織化されているかを記述することが重要です)。伝統的にこのサブフィールドは代数と呼ばれます。
- 空間(幾何学): 物がどこにあるか、形や配置、距離や角度など空間的性質を扱います。ユークリッド幾何から非ユークリッド幾何、微分幾何、位相幾何まで幅広く、図形の性質を抽象化して研究します(ここでは幾何学が当てはまります)。
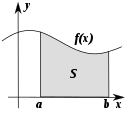
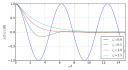
- 変化(解析): 物事がどのように変化するか、連続性や極限、微分・積分、級数、微分方程式などを通じて表現します。古典的にはこの分野を分析と呼び、物理現象のモデル化や最適化問題の理論的基盤を提供します。
さらに広がる分野と手法
これら四つの大きな分類に加えて、現代数学には多くの重要分野があります。たとえば
- 確率・統計: 不確実性とデータ解析に関する理論と方法。
- 数値解析: 実際の計算で近似解を得るためのアルゴリズムと誤差解析。
- 離散数学: グラフ理論や組合せ論、計算理論など、有限・離散構造を扱う分野。
- 位相数学: 変形に対して保たれる性質(連結性、コンパクト性など)を扱う抽象的な空間論。
- 応用数学: 物理学、工学、生物学、経済学などの問題を数学でモデル化し、解析・数値計算・シミュレーションで解を得る分野。
数学の方法論:定義、証明、抽象化
数学は厳密な論理に基づく学問です。主な方法は
- 定義: 対象の意味を正確に定める。
- 公理と構造: 前提となる基本的法則(公理)から理論を構築する。
- 証明: 命題の真偽を論理的に示す。証明は数学的知識の信頼性を担保します。
- 抽象化: 個別の事例から本質を抜き出し、一般的な概念や定理を導く。
- モデリングと計算: 現実の問題を方程式やアルゴリズムに置き換え、解析や数値計算で解決を図る。
数学の応用例
数学は純粋に理論的な興味だけでなく、現実の問題解決に幅広く用いられます。たとえば:
- 物理学や科学全般での理論構築(微分方程式、線形代数、確率論)。
- 工学や建設などの仕事での設計・解析(構造解析、最適化、数値シミュレーション)。
- ビジネスや金融でのリスク評価、最適化、統計解析。
- 情報科学・暗号理論・アルゴリズム設計(離散数学、数論、確率論)。
- データサイエンスや機械学習におけるモデル化・最適化・統計的推定。
- 医療画像処理やバイオインフォマティクスでの信号処理・統計解析。
教育と職業
数学は基礎教育から大学・研究レベルまで幅広く教えられ、論理的思考力や問題解決力を育てます。数学者(あるいは数学に詳しい専門家)以外にも多くの人が数学を学び、利用しています。特に現代では、多くの職業で数学的素養が求められます。ビジネス、科学、工学、建設などの仕事に携わる人々は、数学の基本的な知識と技術を必要とします。
まとめ
数学は「数・構造・空間・変化」という四つの視点を基礎に、抽象化と厳密な証明を通じて体系化された学問です。純粋数学としての美しさや論理的一貫性に加え、応用面では現実世界の複雑な問題を解く強力な道具になります。学習を通じて得られる論理的推論力やモデル化能力は、様々な分野で役立ちます。
数学における問題解決
数学は論理を使って問題を解決します。数学者が使う論理学の主な道具の一つに演繹法があります。推論は、古い真理を使って新しい真理を発見し、証明するための特別な思考法です。数学者にとって、何かが真実である理由(証明と呼ばれる)は、それが真実であるという事実と同じくらい重要であり、この理由は演繹法を使って発見されることが多い。推論を使うことが、実験やインタビューに頼る他の種類の科学的思考とは異なる数学的思考を可能にしているのです。
論理と推論は、数学者が一般的なルールを作るために使うもので、数学の重要な部分です。これらの規則は、一つの規則が多くの状況をカバーできるように、重要でない情報を省いています。一般規則を見つけることで、数学は多くの問題を同時に解決し、これらの規則を他の問題にも利用することができます。これらの規則は、定理(証明されている場合)や推測(まだ真かどうかわからない場合)と呼ばれることがあります。ほとんどの数学者は、論理的な証明を見つけるために、非論理的で創造的な推論を使います。
数学は、私たちがまだ理解していないルールやアイデアを見つけたり、研究したりすることがあります。多くの場合、数学では、アイデアやルールは、それらが単純であると考えられたり、きちんとしていると考えられたりするために選択されます。一方で、数学で勉強した後に、現実の世界でそのような考えやルールが見つかることもあります。一般的に、数学のルールや考え方を勉強することで、世界をよりよく理解することができます。数学の問題の例としては、足し算、引き算、掛け算、割り算、微積分、分数、小数などがあります。代数の問題は、特定の変数を評価することによって解かれます。電卓は、基本的な四則演算ですべての数学の問題に答えます。
数学を学ぶ分野
数
数学は数と量の研究が含まれています。それは形、量、配置の論理を扱う科学の一部門です。以下にリストされている分野のほとんどは、集合論や数学的論理学を含む数学の多くの異なる分野で研究されています。数論の研究は通常、整数の構造と振る舞いではなく、数自体の実際の基礎に焦点を当てているので、このサブセクションには記載されていません。
| 0 , 1 , 2 , 3 , ... | ... ,... - 1 , 0 , 1 , ... | 1 2 , 2 3 , 0.125 , ... | π , e , 2 , ... {displaystyle \pi ,e, {\sqrt {2}}, {\ldots }. | 1 + i , 2 e i π / 3 , ... {displaystyle 1+i,2e^{i\pi /3},\ldots }。 |
| 自然数 | 整数 | 有理数 | ||
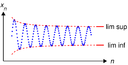
| 埋め合わせをしてくれる人がいないと、「埋め合わせをしてくれる人がいないと、埋め合わせをしてくれる人がいないと、埋め合わせをしてくれる人がいないと、埋め合わせをしてくれる人がいないと、埋め合わせをしてくれる人がいないと、埋め合わせをしてくれない人がいます。 | + ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ | > , ≥ , = , ≤ , < { {displaystyle >,\geq ,=,\leq ,< } }。 | f ( x ) = x {displaystyle f(x)={\sqrt {x}}}}}}。 | |
| 序数 | 枢機卿数 | 算術演算 | 算術関係 |
構造
数学の多くの分野では、物体が持つ構造を研究しています。これらの分野のほとんどは代数学の研究の一部です。
|
|
|
|
|
|
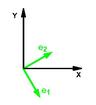
| 数論 | 抽象代数 | 線形代数 | 秩序論 |
形状
数学のいくつかの分野では、物の形を研究しています。これらの分野のほとんどは幾何学の研究の一部です。
|
|
|
|
|
|
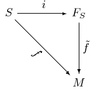
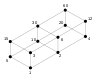
| トポロジー | 微分幾何学 |
変更
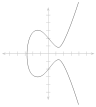
数学のいくつかの分野は、物事の変化の仕方を研究しています。これらの分野のほとんどは分析の研究の一部です。
|
|
|
|
| ベクトル微積分 | ||
|
|
|
|
| 動的システム |
応用数学
応用数学は、工学、物理学、計算機などの他の分野の問題を解決するために数学を使用します。
数値解析 - 最適化 - 確率論 - 統計学 - 数理ファイナンス - ゲーム理論 - 数理物理学 - 流体力学 - 計算アルゴリズム
有名な定理
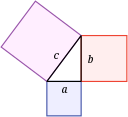
これらの定理は、数学者や数学者ではない人にも興味を持ってもらいました。
ピタゴラスの定理 - フェルマーの最後の定理 - ゴールドバッハの思い込み - 双子素数の思い込み - ゲーデルの不完全性定理 - ポアンカレの思い込み - カントールの対角線上の議論 - 四色定理 - ゾルンのレーマ - オイラーの同一性 - チャーチ・チューリングのテーゼ
これらは、数学を大きく変えた定理や憶測です。
リーマン仮説 - 連続体仮説 - P対NP - ピタゴラスの定理 - 中心限界定理 - 微積分の基本定理 - 代数学の基本定理 - 算術の基本定理 - 射影幾何学の基本定理 - 曲面の分類定理 - ガウス・ボンネットの定理 - フェルマーの最後の定理 - カントロヴィッチの定理
基礎と方法
数学の本質を理解することの進歩は、数学者の学習方法にも影響を与えます。
数学哲学 - 数学的直観主義 - 数学的構成主義 - 数学の基礎 - 集合論 - 記号論理学 - モデル論 - カテゴリ理論 - 論理学 - 逆数学 - 数学記号表
歴史と数学者の世界
歴史の中の数学、数学史の中の数学。
数学の歴史 - 数学の年表 - 数学者 - フィールズメダル - アベル賞 - ミレニアム賞問題(クレイ数学賞) - 国際数学連合 - 数学競技会 - ラテラルシンキング - 数学とジェンダー
数学分野での受賞
数学にノーベル賞はありません。数学者は、重要な業績に対してアベル賞やフィールズメダルを受賞することができます。
クレイ数学研究所は、ミレニアム賞の問題を1つ解いた人に100万ドルを与えると言っています。
数学ツール
数学をするためのツールや、数学の問題の答えを見つけるためのツールはたくさんあります。
古いツール
新しいツール
も参照してください。
- 数学における女性の年表
- アメリカ数学会
- 産業応用数理学会
- 数学の系譜プロジェクト
- 数学科目分類
質問と回答
Q:数学とは何ですか?
A:数学は、数、形、パターンに関する学問です。語源はギリシャ語のμάθημα(máthema)で、「科学、知識、学問」を意味する。
Q:数学の主な分野は何でしょうか?
A:数学の主な分野は、数、構造(代数)、場所(幾何)、変化(解析)です。
Q:数学は実社会でどのように使われているのでしょうか?
A:応用数学は、実社会の問題を解決するのに役立ちます。ビジネス、科学、工学、建設に携わる人々は、数学を使います。
Q:「数学」の略称はあるのでしょうか?
A: はい。イギリス連邦の国々では「maths」、北米では「math」と短縮されることがあります。
Q:「数学」とはどういう意味ですか?
A:「数学」の語源はギリシャ語のμάθημα(máthema)で、「科学、知識、学問」を意味する。
Q:応用数学はどのような問題解決をするのでしょうか?
A: 応用数学は、ビジネス、科学、エンジニアリング、建設などの分野で働く人々が遭遇する実社会の問題を解決するものです。
百科事典を検索する