熱力学第二法則(エントロピー増大の法則):定義とクラウジウス・ケルビンの説明
熱力学第二法則(エントロピー増大)の定義とクラウジウス・ケルビンの説明をわかりやすく解説。原理・例・応用で熱と秩序の本質を理解する入門ガイド
熱力学の第二法則は、エネルギーがある形から別の形に変化したり、物質が自由に動いたりすると、孤立系(外部とエネルギーや物質をやり取りしない系)のエントロピー(系の「無秩序さ」や「可能な状態の広がり」)が増大する傾向があることを述べています。数学的には、孤立系については次が成り立ちます:ΔS ≥ 0。ここで等号は可逆過程に対応し、不等号は不可逆過程(自然に起こる普通の過程)を示します。
エントロピーの直感的な意味
エントロピーは、物質やエネルギーが「どれだけ広く」分布しているかを表す尺度です。温度、圧力、密度の違いなどの差は時間がたつにつれて緩和し、やがて均一化する傾向があります。たとえば、温度や圧力の不均一は水平面に沿って拡散しやすく、重力場では垂直方向に密度や圧力が変化するため完全に均一にはなりません(下方の方が高密度・高圧になります)。これらの緩和はエントロピー増大の具体例です。
クラウジウスとケルビンの表現
熱力学の第二法則の最も一般的な言い回しのひとつは、本質的にルドルフ・クラウジウスによるものです。別の表現としてクラウジウスは次のように述べました:
熱は冷めた体から高温の体には伝わりません。
同様に、ケルビン卿の定式化は機関(熱機関)の観点から次のように表されます:
恒温の熱源から抽出された熱を仕事に変換することだけが最終的な結果となる変換は不可能です。
これらは同じ物理原理の異なる言い方です。クラウジウスの表現は熱の自発的な流れの方向を示し、ケルビンの表現は理想的な熱機関の効率に限界があること(カルノー効率)を示します。
可逆過程・不可逆過程とエントロピー変化
- 可逆過程:理想的・仮想的な過程で、外部条件を無限にゆっくり変えるなどして系と環境の合計エントロピー変化がゼロになります(ΔStotal = 0)。
- 不可逆過程:実際の自然過程で、摩擦、乱流、拡散、自由膨張などによりエントロピーが増大します(ΔStotal > 0)。
定量的な定義
熱的な可逆過程に対して、エントロピー変化は次の式で定義されます:ΔS = ∫ δQ_rev / T。ここで δQ_rev は可逆に加えられる熱、T はそのときの温度(絶対温度)です。エントロピーの単位はジュール毎ケルビン(J/K)です。
統計的(微視的)解釈
ボルツマンの統計的解釈では、エントロピー S は系が取り得る微視的状態の数 W に対して次の関係で与えられます:S = k ln W(k はボルツマン定数)。多くの微視的状態にまたがるほどエントロピーは大きくなり、巨視的に見て「ありふれた」状態ほど高エントロピーになります。第二法則は本質的に確率論的であり、状態数の多い方へ自然に進む確率が非常に高いことを述べています。
適用範囲と例外的現象
第二の法則は大規模(多粒子)の系に非常によく適用されますが、非常に小さい系や短時間では熱揺らぎにより一時的にエントロピーが減少することが観測されることがあります(フラクチュエーション)。また「マクスウェルの悪魔」の思考実験は、第二法則の根底を問い直しましたが、情報の処理に伴うエントロピー生成(ランドアーの原理)を考慮すると矛盾は解消されます。
実用的な意義
- 熱機関の効率には上限があり、カルノー効率がその理想限界を与えます(第二法則に由来)。
- 化学反応や相転移、拡散や混合など多くの自然現象の進行方向や平衡状態を決める際に重要な指標となります。
- エントロピー増大は、時間の矢(時間の一方向性)と密接に結びついています。ミクロでは可逆な力学法則から出発しても、巨視的には不可逆な振る舞いが統計的に現れます。
まとめ
熱力学第二法則は、孤立系においてエントロピーが増大する(または可逆過程で不変である)という経験則であり、エネルギーの変換や物質の拡散、熱機関の限界などを支配する基本原理です。その理解には巨視的な熱力学的記述と微視的な統計的記述の両方が有用で、現代の物理学・工学・情報理論に広く応用されています。
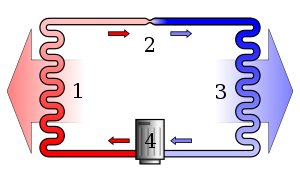
ヒートポンプの蒸気圧縮冷凍サイクルの簡単な様式化された図:1)凝縮器、2)膨張弁、3)蒸発器、4)圧縮機。
概要
一般的な意味では、第二法則では、互いに接触している系間の温度差が均等になる傾向があり、これらの非平衡差から仕事が得られるが、仕事が行われエントロピーが増加すると熱エネルギーの損失が生じるとしている。孤立した系の圧力、密度、温度差は、機会が与えられればすべて均等になる傾向があり、密度と圧力は、温度ではなく、重力の影響を受けます。熱機関は、2つの体の温度差から有用な仕事を提供する機械装置です。
名言
| “ | エントロピーは常に増加するという法則は、自然界の法則の中で最高の位置にあると思います。もし誰かが、あなたの宇宙論がマクスウェルの方程式と不一致であることを指摘したら、マクスウェルの方程式の方がよっぽど悪い。もしそれが観測によって矛盾していることが判明した場合 - まあ、実験家は時々物事を誤魔化すものです。しかし、もしあなたの理論が熱力学の第二法則に反していることが判明した場合、私はあなたに希望を与えることはできません。 | ” |
--アーサー・スタンレー・エディントン『物理世界の性質』(1927年)
| “ | 孤立したシステムでエントロピーが増加する傾向は、熱力学の第二法則で表現されています--おそらく、すべての人間の思考の中で最も悲観的で非道徳的な定式化です。 | ” |
--グレッグ・ヒルとケリー・ソーンリー『プリンキピア・ディゾルディア』(1965年
| “ | 第二法則の定式化は、第二法則についての議論があったのとほぼ同じ数だけあります。 | ” |
--物理学者・物理学者のブリッジマン(1941年)
その他
- フランダースとスワンは、「第一法則と第二法則」と呼ばれる熱力学の第二法則の声明を音楽に合わせて設定したものを制作した。
- 経済学者のニコラス・ジョルゲスク・ローゲンは、経済学の分野でエントロピー法の意義を示した(彼の著作『エントロピー法と経済過程』(1971年)、ハーバード大学出版局参照)。
質問と回答
Q: 熱力学の第二法則とは何ですか?
A: 熱力学の第二法則は、エネルギーがある形態から別の形態に変化したり、物質が自由に移動したりすると、閉じた系のエントロピー(無秩序)が増大するというものです。
Q: 時間の経過とともに水平方向に均等になるものは何ですか?
A: 温度、圧力、密度の差は、しばらくすると水平方向に均等になる傾向があります。
Q: 密度と圧力が垂直方向に均等にならないのはなぜですか?
A: 重力の力により、密度や圧力は垂直方向には均等になりません。下部の密度や圧力は上部より高くなります。
Q: エントロピーとは何ですか?
A: エントロピーとは、物質とエネルギーが、それらがアクセスできるあらゆる場所に広がっていることを示す尺度です。
Q: 熱力学第二法則の最も一般的な表現は何ですか?
A: 熱力学第二法則の最も一般的な表現は、基本的にルドルフ・クラウジウスによるものです。
Q: 熱力学第二法則に関するクラウジウスのもう一つの声明は何ですか?
A: クラウジウスによるもう一つの声明は、熱はそれ自体、より冷たい物体からより熱い物体には伝わらないというものです。
Q: 熱力学第二法則はどのような系に適用されますか?
A: 熱力学第二法則は、エネルギーや物質が出入りしない大きな系にのみ適用されます。系が大きければ大きいほど、第二法則が成り立つ可能性が高くなります。
百科事典を検索する