三角法とは｜定義と歴史、三角関数（sin・cos・tan）の基礎と応用

三角法（ギリシャ語のtrigonon＝3つの角、metron＝尺度）は、角度、三角形、およびサイン（sin）、コサイン（cos）、タンジェント（tan）などの三角関数を扱う初等数学の一部である。幾何学と何らかの関係があるが、その関係については意見が分かれており、三角法は幾何学の一部分に過ぎないとする人もいる。

定義と基本概念

三角法は角度と長さの関係を扱う分野で、特に三角関数（sin, cos, tan）を用いて角度に対する比や座標を表現する方法です。角度は度（°）とラジアン（rad）で表され、1周は360°＝2πラジアンです。

三角関数の基礎（直角三角形と単位円）

  • 直角三角形での定義：斜辺を1とする直角三角形を考えると、角θに対して
    • sin θ = 対辺 / 斜辺
    • cos θ = 隣辺 / 斜辺
    • tan θ = 対辺 / 隣辺 = sin θ / cos θ（cos θ ≠ 0）
  • 単位円（中心が原点、半径1の円）での定義：角θを原点から測ったとき、単位円上の点の座標を(x, y)とすると
    • cos θ = x
    • sin θ = y
    この定義は全ての実数角に対して三角関数を拡張します。
  • 代表値：sin 0 = 0, cos 0 = 1, sin(π/6) = 1/2, cos(π/3) = 1/2, tan(π/4) = 1 など。

主な恒等式と性質

  • ピタゴラス恒等式：sin²θ + cos²θ = 1
  • 加法定理：
    • sin(α ± β) = sin α cos β ± cos α sin β
    • cos(α ± β) = cos α cos β ∓ sin α sin β
  • 二倍角・半角公式：sin 2θ = 2 sin θ cos θ、cos 2θ = cos²θ − sin²θ など
  • 周期性と対称性：sin(θ + 2π) = sin θ、cos(θ + 2π) = cos θ。奇関数・偶関数の性質：sin(−θ) = −sin θ、cos(−θ) = cos θ。

逆三角関数とグラフ

三角関数の逆関数として、arcsin, arccos, arctan（逆正弦・逆余弦・逆正接）が定義され、角度を復元します。三角関数のグラフは周期的で、sinは上下に振れる波形、cosは位相がずれた同様の波形、tanは周期 π の不連続を持ちます。

微分・積分との関係

解析学では三角関数は滑らかな関数として重要です。主な導関数は

  • d/dx sin x = cos x
  • d/dx cos x = −sin x
  • d/dx tan x = sec² x = 1 / cos² x
これらの性質とテイラー級数展開（例：sin x = x − x³/3! + x⁵/5! − …）により数値計算法やフーリエ解析に用いられます。

歴史的背景（概略）

  • 古代ギリシャ・天文学：三角法の起源は天文学的問題のための角度測定にあり、ギリシャの数学者たちが初期の表や法を発展させました。
  • インドやイスラム世界の貢献：インドの数学者（たとえばAryabhataなど）はsinに相当する概念を発展させ、イスラム世界の学者らはこれを受け継ぎ表や計算法を改良しました。
  • ルネサンス以降の発展：ヨーロッパにおける緯度経度測定・海洋航法の必要から三角法は体系化され、解析学の成立とともにより深く発展しました。

応用例

  • 測量・航海・航空：角度と距離の関係を使って位置や方角を求める。
  • 物理学・工学：振動・波動・回転運動の解析（例：単振動の記述にサイン波を使用）。
  • 信号処理・フーリエ解析：周期的信号を三角関数の重ね合わせとして表現する。音声・画像処理にも必須。
  • コンピュータグラフィックス：回転変換や投影変換で三角関数を使用。
  • 数値計算法：テイラー級数やCORDICアルゴリズムによる三角関数の効率的計算。

学習のポイント

  • 直角三角形と単位円の両方の定義を理解すること。
  • 主な恒等式（ピタゴラス、加法定理など）を使って式の変形ができるようにすること。
  • グラフや周期性、対称性を視覚的に把握すること。
  • テイラー展開や導関数を通じて解析的な性質にも触れると応用領域が広がる。

三角法は古代から現代まで数学と科学の基礎を支えてきた重要な分野であり、基礎概念の習得は多くの実務・研究分野で不可欠です。

概要と定義

三角法では、三角形の部分を表現するために多数の具体的な単語を使用します。三角法における定義のいくつかを紹介する。

  • 直角三角形 - 直角三角形は、90度に等しい角度を持つ三角形である。 三角形は1つ以上の直角を持つことはできない）標準的な三角比は直角三角形にのみ使用することができます。
  • 斜辺 - 三角形の斜辺は最も長い辺であり、直角の反対側にある辺である。例えば、右の三角形の場合、斜辺は辺cである。
  • 角の反対側 - 角の反対側とは、その角の頂点と交わらない辺のこと。例えば、辺aは右の三角形の角Aの反対側である。
  • 角の隣接 - 角の隣接辺とは、角の頂点と交差し、斜辺ではない辺のことである。例えば、辺bは右の三角形で角Aに隣接している。
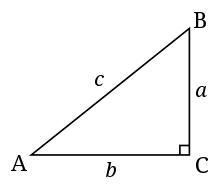
標準的な直角三角形。Cはこの絵の直角Zoom
標準的な直角三角形。Cはこの絵の直角

三角比

直角三角形の三角比は主に3つあり、その逆数も3つあります。合計で6つの比がある。それらは

  • 正弦 (sin) - 角度の正弦はOpposite Hypotenuseに等しい{displaystyle {{text{Opposite｝\Hypotenuse}} {displaystyle {{text{Hypotenuse}} {\displaystyle {{\text{Opposite}} \over {\text{Hypotenuse}}}}
  • コサイン (cos) - 角度のコサインはAdjacent Hypotenuseに等しい{{displaystyle {{text{Adjacent｝\Hypotenuse}} の上に置く。 {\displaystyle {{\text{Adjacent}} \over {\text{Hypotenuse}}}}
  • 接線 (tan) - 角度の接線はOpposite Adjacent {displaystyle} {{text{Opposite｝\୧⃛(๑⃙⃘◡̈๑⃙⃘) {\displaystyle {{\text{Opposite}} \over {\text{Adjacent}}}}

これらの比率の逆数は

コセカント (csc) - 角度のコセカントは Hypotenuse Opposite {displaystyle {{text{Hypotenuse}}} に等しい。{\displaystyle {{\text{Hypotenuse}} \over {\text{Opposite}}}}\csc θ = 1 sin θ {displaystyle ⑅csc ⑅ta ={1 ⑅sin ⑅ta }} に等しくなります。 {\displaystyle \csc \theta ={1 \over \sin \theta }}

secant (sec) - 角度の secant は Hypotenuse Adjacent {displaystyle {{text{Hypotenuse}}} と等�������ります。\over {text{Adjacent}}{\displaystyle {{\text{Hypotenuse}} \over {\text{Adjacent}}}} or sec θ = 1 cos θ {displaystyle \sec \theta ={1 \over \cos \theta }} {displaystyle {text{Adjacent}}} or sec θ = 1 cos θ {displaystyle {text{Adjacent}} {\displaystyle \sec \theta ={1 \over \cos \theta }}

コタンジェント (cot) - 角度のコタンジェントはAdjacent Opposite {displaystyle {{text{Adjacent}}} と等しくなります。{\displaystyle {{\text{Adjacent}} \over {\text{Opposite}}}}\ʕ-̫͡-ʔ ̫͡-ʔ ̫͡-ʔ ̫͡-ʔ ̫͡-ʔ ̫͡-ʔ {\displaystyle \cot \theta ={1 \over \tan \theta }}

この関係を覚えるために、学生はよくニモニックを使う。直角三角形のサイン、コサイン、タンジェントの比は、SOH-CAH-TOAのように文字列で表すことで覚えることができるのです。

正弦波＝対辺÷斜辺

コサイン＝隣接÷斜辺

タンジェント＝反対側÷隣接側

三角法を使って

正弦波と余弦波を使えば、三角形に関するほとんどすべての質問に答えることができる。これを三角形を「解く」という。2つの辺とそれに含まれる角、2つの角と1つの辺、3つの辺が分かれば、どんな三角形でも残りの角と辺を計算することができる。これらの法則は、幾何学のすべての分野で有用である。なぜなら、すべての多角形は三角形の組み合わせとして記述することができるからである。

三角法は、測量、ベクトル解析、周期関数の研究にも不可欠である。

また、球面幾何学を扱う球面三角法というものもある。これは、天文学、測地学、航海術などの計算に使われる。

三角関数の法則

正弦の法則

a Sin A = b Sin B = c Sin C {displaystyle {{text{a}}}\Ίταμμα για για για για για για για για για για\over {}{text{Sin B}}={{text{c}}\over {text{Sin C}} {{text{Sin C}}} {\displaystyle {{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}}

コサインの法則

a 2 = b 2 + c 2 - 2 b c cos ( A ) {displaystyle a^{2}=b^{2}+c^{2}-2bccos(A)} } {displaystyle a^{2}=b^{2}+c^{2}-2bccos(A) {\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos(A)}

タンジェントの法則

a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) ){表示スタイル {frac {a-b}{a+b}}={frac {tan({}frac {1}{2}}(A-B))}{tan({}frac {1}{2}}(A+B))}} {\displaystyle {\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}}


AlegsaOnline.com - 2020 / 2025 - License CC3