単位円とは 定義・方程式(x^2+y^2=1)と性質および三角関数での応用
単位円の定義と方程式 x^2+y^2=1 を図解で丁寧に解説し原点中心・半径1の性質や三角関数での応用と例題をわかりやすく紹介
数学では、半径が1の円を単位円といい、中心は原点(座標(0,0))である。単位円の標準的な方程式は x2 + y2 = 1 で表される。元の表記は次のとおりである: x +2 y = {\\21 x^{2}+y^{
基本的な性質
- 方程式:任意の点 (x,y) が単位円上にあるとは、x2 + y2 = 1 を満たすことを意味する。
- 中心と半径:中心は原点 (0,0)、半径は 1。
- 対称性:x軸、y軸、原点まわりに対して対称。
- 面積と周長:面積は π、周長(円周)は 2π(半径が1のとき)。
三角関数との関係
単位円は三角関数を定義する便利な図形である。原点から角度 θ(通常はラジアン)だけ回転した点は座標 (cos θ, sin θ) で表される。すなわち、任意の実数 θ に対して
(x,y) = (cos θ, sin θ) は自動的に cos2θ + sin2θ = 1 を満たす。これは三角関数の基本恒等式(ピタゴラスの恒等式)である。
パラメトリック表示と向き
- 単位円はパラメータ θ を用いて x = cos θ, y = sin θ と表せる。
- θ が増加すると、点は通常反時計回りに動く(正の向き)。
微分・接線
- 上半分のグラフ y = +√(1 − x2) に対して、微分係数は dy/dx = −x / y(y ≠ 0)。
- パラメトリック表示では、速度ベクトルは (−sin θ, cos θ) であり、これが接線方向を与える。
複素数平面での単位円
複素数平面では、単位円は絶対値(ノルム)が1の複素数全体の集合 {z ∈ C | |z| = 1} である。オイラーの公式により点は eiθ = cos θ + i sin θ と表され、角度 θ と密接に対応する。
応用と注意点
- 単位円は角度の測り方(度とラジアン)や三角関数の周期性、対称性の理解に役立つ。
- 直交座標と極座標の変換(x = r cos θ, y = r sin θ)を学ぶときの基準としても使われる(ここで r = 1 の場合が単位円)。
- 座標平面上の任意の円の方程式は、適切な平行移動や縮尺で単位円に帰着できるため、幾何学的・解析的な議論が簡単になる。
以上が単位円の定義・方程式と基本的性質、ならびに三角関数などへの応用の概要である。
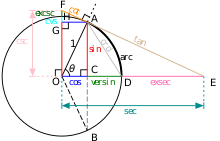
単位円は、あらゆる三角関数のモデルとして使用できます。
単位円における三角関数
単位円の中で、求める角度をtと










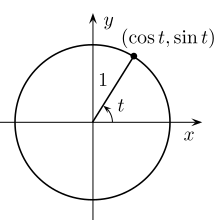
単位円は三角関数の変数の代わりになります。
質問と回答
Q: 単位円とは何ですか。A: 単位円とは半径1の円のことです。
Q: 単位円の方程式は何ですか。
A: 単位円の方程式は x^2 + y^2 = 1 です。
Q: 単位円の中心はどこですか?
A: 単位円の中心は原点、つまり座標(0,0)です。
Q: 数学における単位円の目的は何ですか?
A: 単位円は三角法でよく使われます。
Q: なぜ単位円は重要なのですか?
A: 角度と三角関数の関係を理解するのに役立つからです。
Q: 単位円の半径は何ですか。
A: 単位円の半径は1です。
Q: 単位円の半径が1であることの意味は?
A: 単位円の半径が1であることの意味は、計算を簡単にし、角度と三角関数の値との関係を簡単にすることです。
百科事典を検索する