次元
次元は、私たちが世界を見たり、測ったり、体験したりする方法です。上下、右から左へ、後ろから前へ、暑さと寒さ、重さと長さだけでなく、数学や物理学のより高度な概念を使用しています。次元を定義する一つの方法は、オブジェクトが特定の空間で移動できる自由度や方法を見ることです。次元という用語が使用される概念や方法にはさまざまなものがあり、また、さまざまな定義もあります。すべての概念を満たす定義はありません。
ベクトル空間（ベクトルは開端線）では，次元はベクトルや直線の方向のカーディナリティや数に等しい．また、その空間の直線の方向の最大グループの数にも等しい。日常生活の中での"普通の"物体は，通常，長さ，幅，奥行きの３次元によって規定されている．数学者はこの概念をユークリッド空間と呼ぶ。
寸法を使って位置を測ることもできます。スタート地点から位置までの距離を縦、横、高さ方向に測定することができます。これらの距離は、位置を測るための指標となります。
時空間におけるイベントの位置を示すために、第4の（4D）次元である時間が使用されることがあります。
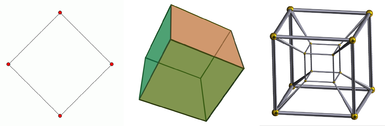
左から正方形、立方体、四次元立方体。正方形は2次元の物体、立方体は3次元の物体、四次元立方体は4次元の物体です。1次元物体は単なる線である．立方体は２次元のスクリーンで見ているので、投影が与えられる。テッセラクトも同様で、三次元空間であっても、追加的に投影としてしか示すことができない。
最初の四つの空間次元の図。
その他の寸法
現代の科学では、人々は別の次元を使用しています。温度や重さのような寸法は、それほど単純ではない空間の中で何かの位置を示すために使用することができます。科学者は次元分析を用いてこれらの次元を研究しています。
数学者も次元を使う。数学では次元の方が一般的です。数学における次元は、世界の物事を測るものではないかもしれません。数学における次元を使った算術のルールは、通常の算術のルールとは異なるかもしれません。
寸法とベクトル
ベクトルは距離や方向を示すのに使われます。ベクトルは工学や科学でよく使われますが、数学でも使われることがあります。
ベクトルは数のリストです。各次元には1つの数があります。ベクトルには算術規則があります。
例えば、ジェーンがサリーの位置を知りたければ、サリーはジェーンに位置を示すベクトルを与えることができる。ジェーンとサリーが世界にいるとすると、三次元があります。したがって、サリーは自分の位置を示す3つの数字のリストをジェーンに与えます。サリーがジェーンに与えるベクトルの中の3つの数字は次のようなものかもしれません。
- サリーのジェーン北の距離
- ジェーンから見たサリーの東の距離
- サリーの身長がジェーンより上
質問と回答
Q:次元とは何ですか?
A: 次元とは、上下、左右、前後、暑さ寒さ、重さ、長さといった概念を用いて世界を測定し、見て、経験する方法です。また、自由度や物体が特定の空間で動くことができる方法として定義することもできます。
Q:数学者はユークリッド空間をどのように定義しているのですか?
A:数学者はユークリッド空間を、通常、長さ、幅、深さと呼ばれる3つの次元によって規定されると定義している。
Q: ベクトル空間におけるベクトルの数は何個ですか?
A:ベクトル空間のベクトルの数は、その基底集合の基数（またはベクトルの数）に等しくなります。
Q:位置の測定には何次元が使われるのか?
A:3次元（縦・横・高さ）です。場合によっては、時間と空間における事象の位置を示すために、4次元（時間）が使われることもある。
Q:dim(V)とはどういう意味ですか?
A: Dim(V)とは、Vの次元のことで、その基底集合の基数（またはベクトルの数）、または、その基底集合が持つ直線の方向の数に等しい。
Q:次元に関連するすべての概念を満たす1つの定義はありますか?
A:ありません。次元に関するすべての概念を満たす単一の定義はありません。
