フラクタル

例

フラクタルには多くの種類があり、多種多様な方法で作られています。例えば、シェルピンスキーの三角形は、大きな三角形の中に小さな三角形が無数に存在する。また、ブノワ・マンデルブロにちなんで名づけられたマンデルブロ集合もその一つである。シェルピンスキーの三角形はパターンで構成されているが、マンデルブロ集合は方程式に基づいている。

また、木々や雪の結晶、一部の野菜や海岸線など、自然界にもフラクタルは多く存在します。

コッホ曲線

コッホ曲線は、フラクタルの簡単な例です。まず、直線の一部から始めます。これを直線セグメントと呼びます。この直線を同じ大きさの3つの断片に切り分けます。そのうちの真ん中を取り除き、切り取った部分と同じ長さの辺を持つ三角形の上の部分を入れます。これで、両端が接した4本の線分ができました。最初の線分に対して行ったことを、4つのビットにそれぞれ行うことができます。同じことを、最終的に得られるすべてのビットに何度も行います。これをずっと続けて、最終的に何ができるか見てみましょう。

コッホ曲線の長さは無限大で、コッホ曲線の面積はゼロです。これはかなり不思議なことである。長さ1、幅1の正方形（寸法は2）は、面積1、長さ無限大となる。

類似性寸法

つまり、コッホ曲線は、1次元のものよりは大きく、2次元のものよりは小さいようです。類似次元の考え方は、フラクタルについて、長さや面積をよりよく理解できるような次元を与えることである。ですから、コッホ曲線には、1 と 2 の間の次元が必要です。

コッホ曲線は4つに切り分けられ、それぞれの大きさは元の大きさの1 3 {displaystyle {frac {1}{3}}} である。フラクタルが切り分けられる個数のことを N {\displaystyle N} 、大きさの差のことを B {\displaystyle B} と呼ぶことにします。これらを式にすると

log N - log B {displaystyle {displaystyle {displaystyle {log N}{-log B}}}}

ここで、log {displaystyle \log } はある数値の対数である。この数はフラクタルのHausdorff Dimensionです。コッホ曲線ではlog 4 - log 1 3 = 1.2619...です。{displaystyle { {frac {}log 4}{-log {frac {1}{3}}}}=1.2619...} 私たちが望んだように。

コッホ曲線は最も単純なフラクタル図形の一つなので、その次元を計算するのは簡単である。その相似次元とハウスドルフ次元はともに同じである。しかし、より複雑なフラクタル図形ではそうではありません。

コッホの雪

コッホ曲線は、線分ではなく正三角形から始まることを除けば、コッホ雪片（またはコッホ星）と同じである。

コッホ曲線の作り方

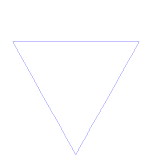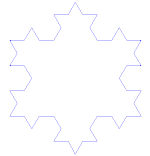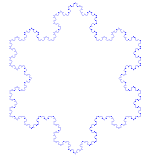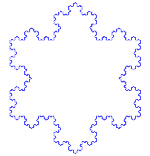
用途

フラクタルは、生物学（肺、腎臓、心拍変動など）、地震、いわゆるヘビーテール分布に関連する金融、物理学など、多くの応用分野がある。このことは、なぜフラクタルが自然界に頻繁に現れるのかを理解するために、フラクタルが研究されるべきことを示しています。

フラクタルには芸術的な理由だけで存在するものもあるが、非常に有用なものもある。フラクタルは無線アンテナの形状として非常に効率的であり、すべての部品を効率的に接続するためにコンピュータチップに使用されている。また、海岸線もフラクタルと考えることができます。