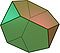
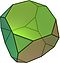
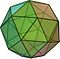
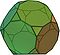
アルキメデス立体（半正多面体）とは：定義・特徴・全種類一覧

アルキメデス立体（半正多面体）の定義・特徴を図解でわかりやすく解説。全種類一覧と発見史、分類や生成法まで一挙掲載。

著者: Leandro Alegsa

31-01-2026 18:12

幾何学上、アルキメデス立体とは、多角形で構成された凸型の形状である。多面体であり、次のような性質を持つ。

各面は正多角形で構成されており
形のすべての角が同じに見える
その形は、プラトン固体でもなく、プリズムでもなく、アンチプリズムでもない。

数え方によっては、13個、15個の形があります。そのうちの2つは、回転しても合同にならない2つのバージョンがあります。アルキメデス立体は、紀元前3世紀に発見したとされる古代ギリシャの数学者アルキメデスにちなんで名付けられました。アルキメデスの著作は失われているが、4世紀にアレキサンドリアのパッポスがまとめている。ルネッサンス期には、芸術家や数学者が純粋な形を重んじ、これらの形をすべて再発見しました。ヨハネス・ケプラーがこの探索を完成させたのは1620年頃であろう。

アルキメデスの立体を構成するには、少なくとも2種類の多角形が必要です。

定義と重要な特徴

正多角形の面からなる：各面は正三角形・正方形・正五角形などの正多角形で構成されます（ただし面の種類は1種類だけではない）。
頂点均一（頂点同形、vertex‑transitive）：どの頂点を見ても周囲の面の並び方が同じであり、頂点の取り扱いはすべて同等です（「形のすべての角が同じに見える」に相当する性質）。
プラトン立体や（通常の）プリズム・アンチプリズムとは区別される：プラトン固体（正多面体）は全ての面が同じ種類の正多角形で構成されますが、アルキメデス立体は複数種類の正多角形を持ちます。また、単純なプリズムやアンチプリズム群は古典的定義では除外されます。
凸で一様（uniform）な多面体の一群：より一般的な「一様多面体」のうち、面がすべて正多角形であり、頂点群が一様な凸多面体のクラスがアルキメデス立体に相当します。
組合せ的に有限個のみ：凸なアルキメデス立体は（鏡像を同一視するかどうかで）13個または15個だけ存在します。

全種類一覧（凸アルキメデス立体：13種）

古典的に「アルキメデス立体」として挙げられる凸の種類は次の13種です（鏡像を別個に数えると15になる）。以下は代表的な英名（慣用名）での一覧です。

Truncated tetrahedron（切頂四面体）
Cuboctahedron（カブオクタヘドロン / 立方八面体）
Truncated cube（切頂立方体）
Truncated octahedron（切頂八面体）
Rhombicuboctahedron（ロムビックキュボオクタヘドロン）
Truncated cuboctahedron（切頂カブオクタヘドロン / 大ロムビック立方八面体）
Snub cube（スナブ・キューブ、左右一対の鏡像を持つ）
Icosidodecahedron（イコシドデカヘドロン / 二十面十二面相互体）
Truncated dodecahedron（切頂十二面体）
Truncated icosahedron（切頂二十面体、サッカーボール型）
Rhombicosidodecahedron（ロムビコシデカヘドロン）
Truncated icosidodecahedron（切頂イコシドデカヘドロン / 大ロムビコシデカ型）
Snub dodecahedron（スナブ・デカ、左右一対の鏡像を持つ）

上のうち Snub cube と Snub dodecahedron は鏡像（右手系・左手系）が互いに非合同であるため、鏡像を別個に数えると総数が15になります。

簡単な解説（構造と表記）

頂点まわりの面の並びは「頂点記号（vertex configuration）」で表されます（例：3.3.3.3.3は正五角形が5つ、など）。アルキメデス立体では各頂点の記号が全て同じになります。
オイラーの多面体定理 V − E + F = 2（V：頂点数、E：辺数、F：面数）や対称性の考察を用いて、可能な組合せを列挙・分類できます。この手法が、なぜ有限個しか存在しないかを説明します。

歴史と学問的意義

「アルキメデス立体」の概念は古代ギリシャのアルキメデス時代に遡るとされますが、元の著作は現存していません。4世紀のパッポスがまとめた記述がその伝承を伝え、ルネサンス期に芸術家や数学者が再発見・研究を行い、ヨハネス・ケプラーらがさらに研究を進めました。近代になって群論や組合せ論、位相的制約（オイラーの式）を用して厳密に分類・証明されました。

応用例と関連分野

化学：フラーレン（C60）は切頂二十面体（truncated icosahedron）に近い構造を持ち、分子構造の理解や材料科学に影響を与えています。
建築・デザイン：ドームや装飾、モザイク構成などで対称性と美的性質を活用できます。
教育：多面体の対称性・多角形の療法の学習に利用され、幾何学的直感を養う題材となります。

補足：定義の範囲

現代の文献では「アルキメデス立体」を定義する際に、凸であること、面が正多角形であり頂点が一様であることを条件にするのが一般的です。プリズムやアンチプリズム、プラトン立体は古典的定義では除外されますが、文献や分野によって用語の扱いに差があるため、定義の注記を確認することが重要です。

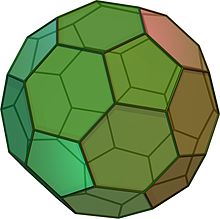
正20面体は、サッカーボールのような形をしています。正五角形12個と正六角形20個で構成されています。頂点数は60、辺数は90です。アルキメデスの立体です。

プロパティ

アルキメデス立体は、正多角形でできているので、すべての辺が同じ長さになります。
すべてのアルキメデス立体は、プラトン立体の「縁を切る」ことで、プラトン立体から作り出すことができます。
アルキメデス立体とプラトン立体の特徴は、角（頂点）で出会う多角形のタイプです。

プラトニック固体との関係

プラトン立体は、一連の構造規則に従うことでアルキメデス立体になります。

アルキメデス立体は、万華鏡の発電機の位置のように構成することができます。

アルキメデスの立体の一覧

以下は、すべてのアルキメデス立体のリストです。

イメージ	名前	顔	タイプ	エッジ	頂点
	切断された四面体	8	4つのトライアングル 4つのヘキサゴン	18	12
	Cuboctahedron	14	8つのトライアングル 6つの正方形	24	12
	切断された立方体	14	8つのトライアングル 6オクタゴン	36	24
	切断された八面体	14	6つの正方形 8個のヘキサゴン	36	24
	Rhombicuboctahedron	26	8つのトライアングル 18個の正方形	48	24
	切り詰められた正八面体	26	12つの正方形 8個のヘキサゴン 6オクタゴン	72	48
	スナッブ・キューブ（2つのミラー・バージョン）	38	32個のトライアングル 6つの正方形	60	24
	Icosidodecahedron	32	20個のトライアングル 12個のペンタゴン	60	30
	切断された正十二面体	32	20個のトライアングル 12デカゴン	90	60
	切断された正二十面体	32	12個のペンタゴン 20個のヘキサゴン	90	60
	Rhombicosid12面体	62	三角形20個、四角形 30個、五角形12個	120	60
	切断された正二十面体	62	30個の正方形 20個のヘキサゴン 12デカゴン	180	120
	スナッブ正十二面体（鏡面2枚組）	92	80個のトライアングル 12個のペンタゴン	150	60