線形回帰
線形回帰は、従属変数と1つ以上の説明変数の間の関係を直線を用いて説明する方法である。これは、回帰分析の特殊なケースです。
線形回帰は、厳密に研究された最初の回帰分析のタイプです。これは、未知のパラメータに線形に依存するモデルの方が、パラメータに非線形に関連するモデルよりも適合しやすいからである。さらに、結果として得られる推定量の統計的特性を決定しやすくなります。
線形回帰には多くの実用的な用途があります。ほとんどのアプリケーションは、以下の2つの大まかなカテゴリのいずれかに分類されます。
- 線形回帰は、観察された値（データ）の集合に予測モデルを適合させるために使用できる。これは，目標が予測，予測，削減である場合に有用である．このようなモデルを開発した後で，Xの追加値が，それに付随するyの値なしで与えられた場合，フィットされたモデルを使用して，yの値の予測を行うことができる．
- 変数 y と y に関連しているかもしれない数の変数 X1, ...., Xp が与えられると、線形回帰分析は、y と Xj の間の関係の強さを定量化し、どの Xj が y とまったく関係がないかを評価し、どの Xj のサブセットが y についての冗長な情報を含むかを識別するために適用できます。
線形回帰モデルは、線とデータ点（残差など）の間の垂直距離をできるだけ小さくしようとします。これは、"データに線をフィットさせる"と呼ばれています。しばしば、線形回帰モデルは残差の2乗和（最小2乗）を最小化しようとしますが、他にもフィットの方法があります。それらには、他のノルム（最小絶対偏差回帰のように）で"適合の欠如"を最小化する方法や、リッジ回帰のように最小二乗損失関数のペナルティ付きバージョンを最小化する方法があります。最小二乗法は、線形ではないモデルの適合にも使用できる。上で概説したように，"最小二乗"と"線形モデル"という用語は密接にリンクしているが，同義語ではない．
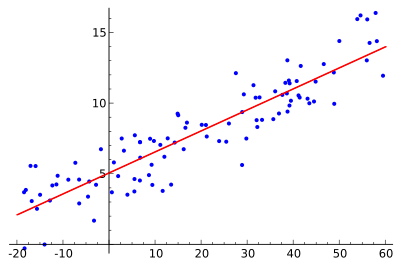
アイデアは、赤い曲線を見つけることであり、青い点は実際のサンプルです。線形回帰では、すべての点を1本の直線で結ぶことができます。この例では、赤線と各サンプル点の間の距離の二乗が最小化される単純な線形回帰を使用しています。
質問と回答
Q:線形回帰とは何ですか?
A: 線形回帰は、数学を使って、他のものが変化したときに何かがどのように変化するかを見る方法です。従属変数と1つ以上の説明変数を用いて、「回帰線」と呼ばれる直線を作成します。
Q: 線形回帰の利点は何ですか?
A: 未知のパラメータに線形的に依存するモデルは，そのパラメータに非線形的に関連するモデルよりも適合しやすい．さらに，得られる推定量の統計的性質が決定しやすい．
Q: 線形回帰の実用的な使用方法は何ですか?
A: 線形回帰は，予測，予想，削減を行うために，観察された値（データ）に予測モデルを適合させるために使用できる．また、変数間の関係の強さを定量化し、別の変数に関する冗長な情報を含むデータのサブセットを識別するために使用することもできます。
Q: 線形回帰モデルは、どのように誤差を最小化しようとするのですか?
A: 線形回帰モデルは，直線とデータ点の間の垂直距離（残差）をできるだけ小さくしようとする．これは，残差の2乗和（最小2乗），他の規範における適合の欠如（最小絶対偏差），または最小2乗損失関数の罰則付きバージョン（リッジ回帰）のいずれかを最小化することによって行われる．
Q: 線形回帰モデルが最小二乗法に基づかないことは可能ですか?
A: はい、線形回帰モデルが最小二乗法に基づくのではなく、他の規範における適合度の欠如を最小化する方法（最小絶対偏差）や最小二乗損失関数のペナルティ版を最小化する方法（リッジ回帰）などを使用することは、可能です。
Q:「線形モデル」と「最小二乗法」は同義語ですか?
A: いいえ、同義語ではありません。線形モデル」は直線を使うことを意味し、「最小二乗」は直線とデータ点の間の垂直距離を最小にすることによって誤差を最小にしようとすることを意味します。
