メルカトル図法とは：原理・歴史・歪みの原因と地図への影響

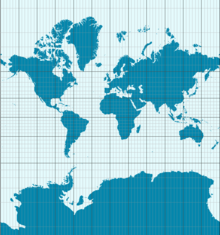
メルカトル図法は、現在、地図製作で広く使われている円筒形の地図投影法である。1569年にGerardus Mercatorによって開発された。物理的な投影法ではないので、幾何学的な道具を使って構築することはできない。小さなスケールでは、幾何学的な図形を歪ませることなく、地図上で動かすことができる（この性質はコンフォーマティと呼ばれる）。欠点として、図形を移動させると、図形の縮尺や線の方向が変わることがあります。例えば、アフリカは実際にはグリーンランドの15倍の広さがありますが、この地図投影図では同じ大きさに見えます。

現在、メルカトル図法は主に地図に使われている。

原理（どうしてこうなるのか）

メルカトル図法は角度（方位）を保つ「コンフォーマル」投影法です。つまり、極めて小さな領域では角度や形が正しく保存されますが、面積は保存されません。結果として、緯度が高くなるほど縦方向の拡大が大きくなり、極に近づくほど面積の歪みが無限に大きくなります。これにより、緯度の高い地域（グリーンランドや北欧など）は実際よりも非常に大きく表示されます。

航法上の利点としては、一定方位（一定のコンパス方位）で進む航路＝ロキソドローム（舵角一定の線）が地図上で直線として表される点が挙げられます。したがって、船や飛行機の航海図で方位をそのまま引ける点が伝統的に重宝されました。

数学的な概要（簡潔に）

• 経度 λ はそのまま横方向の座標（x）に対応します。
• 緯度 φ に対する縦方向の座標 y は、球体モデルなら y = ln(tan(π/4 + φ/2)) のような関数で与えられ、緯度が高くなるほど y が急激に増大します。
• 縮尺因子は緯度 φ に対しておおよそ 1 / cosφ（＝secφ）に比例して大きくなり、極では無限大になります。

歴史的背景

• 1569年、フランドルの地図製作者Gerardus Mercatorが航海用に考案しました。彼の目的は、海図上で一定方位の航路を直線で表すことにありました。
• 長年にわたり海図の標準として使われ、18〜19世紀の大洋航海で重要な役割を果たしました。
• 現代ではナビゲーション以外にも、Web地図（「Web Mercator」など）で広く採用されています。ただしWeb向けの変種は球体モデルを使うなど実装上の差異があります。

歪みの原因と地図への影響

• 面積の歪み：コンフォーマルであるため面積は保存されません。高緯度ほど実際より過大表示されます。たとえば、アフリカ大陸（約3,037万 km²）はグリーンランド（約216万 km²）よりおよそ14倍広いですが、メルカトル図では両者が同程度に見えることがあります（元の文章では15倍と表記）。
• 形状の局所保存：局所的な角度や形は保持されるため、方向や小領域の形状比較には有利です。
• 極の表現不可：極点はyが無限大になるため投影できません。通常は緯度の上限（例えば±85°程度）で表示を切ります。
• 政治的・教育的影響：高緯度地域が大きく見えることにより、世界観や認知に偏りを与えるとの批判（ヨーロッパや北米中心の印象を助長するなど）があります。

現代における用途と問題点

• 航海用、海図では歴史的に重要だったが、現在の海図では等角航路以外の手法も多用されます。
• Web地図（Google Maps や OpenStreetMap などが採用する「Web Mercator（EPSG:3857）」）は表示性能と整合性のためにメルカトルを基にした投影を採用しています。これによりズームやタイル表示が扱いやすくなる反面、世界地図表示での面積誤解は残ります。
• 教育や国際比較の場面では、面積保存（等面積）投影や妥協投影（Winkel Tripel、Robinsonなど）を使うことが推奨される場合があります。

代替投影法（一例）

• 等面積投影（例：ガル＝ペルソン投影、モルワイデ投影）— 面積比較を正確に示したい場合に有効。
• 妥協投影（例：ロビンソン投影、ウィンケル＝トリプル投影）— 形状・面積・距離のバランスを取る。

まとめ：いつ使うべきか

• 使うべき場面：航法（一定方位の航路）、オンライン地図サービス（ズームやタイル管理）、局所的な方位・角度を重視する地図。
• 避けるべき場面：世界規模で面積比較を行うときや、地政学的な誤解を避けたい教育的資料など。

メルカトル図法は数学的に扱いやすく視覚的に直感的な面がある一方で、面積歪みという重大な欠点を持っています。用途に応じて適切な投影法を選ぶことが重要です。

文字で検索