ミンコフスキー時空とは — 特殊相対性理論の4次元時空をわかりやすく解説
ミンコフスキー時空を初心者にも図解で徹底解説。特殊相対性理論の4次元時空、計量(-+++)、平坦時空と一般相対性理論との違いをやさしく紹介。
特殊相対性理論において、ミンコフスキー時空はヘルマン・ミンコフスキーによって作られた4次元の多様体である。空間（x、y、z）の3次元と時間の1次元の計4次元を持つ。ミンコフスキー時空は測度記号が(-+++)であり、質量が存在しない場合の平坦な表面を記述する。この記事では、ミンコフスキー時空を単に時空と呼ぶのが慣例となっている。
しかし、ミンコフスキー時空が適用されるのは、特殊相対性理論においてのみである。一般相対性理論では、重力や加速度運動の影響を記述するために、曲がった時空という概念が用いられた。
基本的な考え方
ミンコフスキー時空は「時間と空間をまとめて扱う」ための数学的な舞台です。点（イベント）は「どこで、いつ起きたか」を表し、これを4つの座標 (t, x, y, z) で表します。時間成分は他の空間成分と同じように扱われますが、計量の符号が負になることで時間の性質が区別されます。
時空間隔（イントリンシックな距離）
二つのイベント間の「時空間隔」s^2 はミンコフスキー計量で定義され、標準的には
s^2 = -c^2 (Δt)^2 + (Δx)^2 + (Δy)^2 + (Δz)^2
の形を取ります（光速 c を 1 とする単位系を使うことも多い）。この量はローレンツ変換に対して不変であり、すべての慣性系で同じ値を取ります。時空間隔の符号によって、二つのイベントが次のように分類されます：
- 時刻的（timelike）：s^2 < 0。因果的につながり、ある慣性系で時間順が変わらない。質量を持つ粒子の世界線はこの領域内。
- 光様（lightlike / null）：s^2 = 0。光や電磁波が伝わる経路。
- 空間的（spacelike）：s^2 > 0。因果的な影響を与えられない距離で、因果順序は慣性系によって変わり得る。
光錐と因果律
あるイベントを基準にすると、その周りに描かれる光錐（light cone）は、そのイベントから出発して光が到達し得る領域と、そこから光が到達できる領域を示します。過去光錐は因果的に影響を及ぼす可能性のある過去のイベントを、未来光錐は影響を受ける可能性のある未来のイベントを表します。この構造が因果律（因果関係のルール）を保証します。
ローレンツ変換と不変量
ミンコフスキー時空での物理法則は、異なる慣性系（等速直線運動する観測者）に対して同じ形を保ちます。これを表すのがローレンツ変換です。時空間隔 s^2 や 4元ベクトルの内積はローレンツ変換に対して不変であり、これが特殊相対性理論における物理量の普遍性の基礎になります。
4元（フォー・ベクトル）と物理量
ミンコフスキー時空では、時間と空間の成分を合わせた4元で物理量を表現します。代表的な例：
- 位置四元：x^μ = (ct, x, y, z)
- 速度四元（4-velocity）：慣性運動における世界線の接ベクトル。固有時で正規化される。
- 運動量四元（4-momentum）：p^μ = (E/c, p_x, p_y, p_z)。不変量 p^μ p_μ = -m^2 c^2 が質量 m を与える。
これらの4元を用いることで、エネルギー・運動量保存則や力学法則が簡潔かつ普遍的に記述できます。
幾何学的な直観：平坦性と直線運動
ミンコフスキー時空は「平坦」な時空です。これは、重力や曲がりがなければ自由運動する物体の世界線は直線（より正確には、計量に対する測地線）になることを意味します。重力が無視できる小さな範囲や、重力場が弱い場合にはミンコフスキー時空が良い近似となります。
視覚化：ミンコフスキー図
直感的には、時間軸を縦、空間軸を横にとった平面に世界線や光錐を描くことで理解しやすくなります。こうした図を「ミンコフスキー図」と呼び、因果関係や同時性の概念、ローレンツ収縮や時間の遅れを視覚的に示すのに役立ちます。
限界と一般相対性理論への拡張
ミンコフスキー時空は重力の効果を含みません。重力が重要な場合、空間と時間は物質・エネルギーによって曲げられ、局所的にはミンコフスキー時空に似ていても全体としては曲がった時空（リーマン多様体）になります。これが一般相対性理論では導入される考え方です。
まとめ
- ミンコフスキー時空は特殊相対性理論の舞台となる平坦な4次元時空で、計量の符号は(-+++)。
- 時空間隔や光錐の概念が因果律と観測者間の不変性を支える。
- 4元を使うことでエネルギー・運動量や運動の法則が簡潔に表現できる。
- 重力がある場合は一般相対性理論の曲がった時空に拡張される。
より詳しい数式や図を使った説明を読みたい場合は、ローレンツ変換、計量テンソル、4元演算に関する入門書や解説を参照すると理解が深まります。
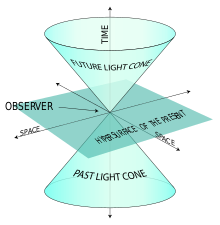
ライトコーンの例。
定義(s)
数学的
時空は4次元の座標系と考えることができ、その軸は次のように与えられる。
( c t , x , y , z ) {displaystyle (ct,x,y,z)}. 
また、以下のように表記することもできます。
( x 1 , x 2 , x 3 , x 4 ) {displaystyle (x_{1},x_{2},x_{3},x_{4})} }. 
ここで、x 1 {displaystyle x_{1}}
は c t {displaystyle ct}
を表しています。光速に時間座標をかけた単位で時間を測るのは、時間の単位が空間の単位と同じになるようにするためである。時空は弧の長さの微分が次式で与えられます。
d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}}. 
このことは、時空が次のように与えられるメトリックテンソルを持つことを意味する。
g u v = [ - 1 0 0 0 1 0 0 0 1 0 0 0 0 1 ] {displaystyle g_{uv}={{begin{bmatrix}-1&0&0&0}&1&0&0}&0&1&0}} [ }} {displaystyle g_{uv}={bmatrix}-1&0&0}&0}&0{bmatrix}-2&0&1 
先に述べたように、時空はどこまでも平坦であり、ある程度は平面と考えることができる。
シンプル
時空は、宇宙のあらゆる事象が起こる「場」と考えることができる。時空間の点を特定するのに必要なのは、ある時間と典型的な空間的方向だけである。4次元を視覚化するのは難しい（事実上不可能）のだが、以下の方法で、ある程度類推することができる。
時空間ダイアグラム
ヘルマン・ミンコフスキーは、ミンコフスキー時空における座標系をグラフ化するためのある方法を紹介した。右図のように、異なる座標系では、物体の空間的な向きや時間的な位置が一致しません。この図からわかるように、空間軸（x軸）と時間軸（ct軸）は一つしかない。必要であれば、さらに空間軸（y軸）を導入することもできますが、残念ながらこれが次元数の限界で、4次元のグラフは描けません。ミンコフスキー時空でのグラフの書き方は、次のようなルールになっている。
1) x軸とx'軸のなす角は t a n ( α ) = v c {displaystyle tan(\alpha )={degrac {v}{c}}}
ここで、vは物体の速度です。
2) 時空を進む光の速度は、どちらの軸に対しても常に45度の角度を作る。
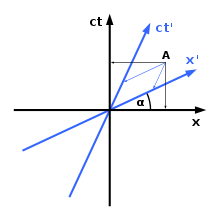
相対性理論では、両観測者はAでの事象を異なる時間に割り当てています。
一般相対性理論における時空
アインシュタインは一般相対性理論において、次のような方程式を用いた。
R u v - 1 2 g u v R = 8 π T u v {displaystyle R_{uv}-{@frac {1}{2}}g_{uv}R=8@pi T_{uv}} 
時空を実際に曲げることができ、その結果、重力の効果が得られること。
関連ページ
| オーソリティコントロール |
|
質問と回答
Q:ミンコフスキー時空とは何ですか?
A: ミンコフスキー時空はヘルマン・ミンコフスキーによって作られた4次元の多様体です。3次元の空間（x, y, z）と1次元の時間を持っています。
Q: ミンコフスキー時空の測度記号は何ですか?
A: ミンコフスキー時空の測度記号は（-+++）である．
Q: ミンコフスキー時空はどのように平坦な表面を表現するのだろうか?
A: 質量がないとき、ミンコフスキー時空は平らな面を表現する。
Q: ミンコフスキー時空は一般相対性理論に適用されるか?
A: ミンコフスキー時空は特殊相対性理論にのみ適用される．一般相対性理論では、重力や加速度運動の効果を記述するために、曲がった時空の概念を用います。
Q:ミンコフスキー時空は何次元ですか?
A:ミンコフスキー時空は、3次元の空間（x、y、z）と1次元の時間の4つの次元を持っています。
Q:ミンコフスキー時空は誰が作ったのですか?
A: ヘルマン・ミンコフスキーがミンコフスキー時空という概念を創り出しました。
百科事典を検索する