時空とは？ミンコフスキー空間と相対性理論で理解する時空間の定義

時空とは何かをミンコフスキー空間と相対性理論で丁寧に解説。空間と時間の結合、速度・重力が時の流れに与える影響を図解でわかりやすく紹介。

著者: Leandro Alegsa

13-12-2025 03:45

時空間とは、空間と時間を連続体と呼ばれる一つのアイデアに結合した数学的モデルである。この4次元の連続体はミンコフスキー空間として知られている。時空間では「出来事（event）」という点が基本的な要素で、これには位置（空間座標）と出来事が起きた時刻（時間座標）の両方が含まれる。出来事同士の間隔は、光速 c を用いた不変量である「間隔（invariant interval）」で表され、特殊相対性理論ではこの間隔がすべての慣性系で同じ値を持つという性質が中心になる。

ミンコフスキー空間の性質

ミンコフスキー空間はユークリッド空間とは異なり、時と空間の成分の符号が異なる計量（ミンコフスキー計量）を持つ。典型的には間隔 s^2 を次のように表す（符号規約により表現は異なる）: s^2 = -c^2Δt^2 + Δx^2 + Δy^2 + Δz^2。ここで s^2 の正負により、時空内での出来事の因果関係（因果的、光様、空間的分離）が決まる。光錐（light cone）は、ある出来事から光が到達し得る領域を示し、この構造が因果律と情報伝播の限界を規定する。

相対性理論と時空

この2つのアイデアを組み合わせることで、宇宙論は、銀河などの大きなレベルと原子などの小さなレベルでの宇宙の仕組みを理解することができました。特殊相対性理論は等速直線運動をする観測者間での時空の振る舞いを記述し、時間の遅れ（time dilation）や長さの収縮（length contraction）、同時性の相対性といった直感に反する現象を導く。さらに、一般相対性理論では重力が時空の曲がり（曲率）として表され、質量・エネルギーの分布が時空の幾何学を決めることで物体の運動や光の経路が説明される。

古典力学との違い

非相対論的な古典力学では、時空の代わりにユークリッド空間を使用するのが良いとされています。なぜなら、時間は普遍的なものとして扱われ、観察者の運動状態に依存しない一定の通過速度を持つからです。ガリレイ変換の下では時間は全ての慣性系で同一であり、速度の合成法則も単純です。しかし、光速に近い速度や強い重力場では古典力学は破綻し、相対論的な説明が必要になります。

時間と速度、重力の影響

しかし、相対論的な宇宙では、時間を3次元の空間から切り離すことはできない。なぜなら、時間の経過の速さは、観測者に対する物体の速度に依存するからです。また、重力場の強さによって、重力場の外にいる観測者から見た物体の時間の流れが遅くなります。これが「時間の遅れ（重力赤方偏移／重力時間遅延）」で、地球近傍の精密な実験（GPS衛星の時刻補正など）でも観測されます。

具体例と応用

GPS：衛星の時計は衛星の速度による特殊相対論的遅れと、地上より弱い重力場に置かれることによる一般相対論的進みの両方を補正する必要がある。
素粒子実験：宇宙線由来のミュー粒子が大気中で観測されるのは、高速移動に伴う寿命延長（時間の遅れ）のおかげである。
天文観測：重力レンズやブラックホール周辺での光の赤方偏移・軌道の摂動など、時空の曲率を直接的に検証する観測が行われている。

まとめ

時空間の概念は、空間と時間を分けて扱う古典的直感を超え、観測者の運動状態や重力の存在によって互いに影響し合う統一的な舞台を提供する。ミンコフスキー空間はその基礎を与え、一般相対性理論はさらに時空が物質・エネルギーによって曲げられることを示す。現代の物理学と技術は、この時空の理解に依拠して発展している。

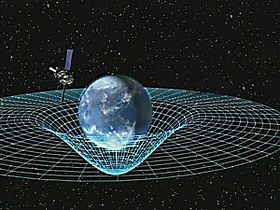
地球による時空間湾曲の説明図。

更なる側面

物質が存在するところでは、時空の幾何学的形状が曲げられます。その結果、時空が曲がった形になり、それが重力として理解できるのです。右の写真の白い線は、質量が時空に及ぼす影響を表しています。

古典力学では、時間はユークリッド空間の3次元の動きとは無関係であるため、時空の使用は任意である。しかし、物体が光速に近い速度（相対論的速度）で動いている場合、時間を3次元空間から切り離すことはできない。静止している観察者から見た時間は、物体がどれだけ光速に近い速度で動いているかによって決まる。

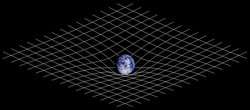
時空間の歪みの2次元的なアナロジー

歴史的由来

時空間というと、1905年に特殊相対性理論を提唱したアインシュタインを思い浮かべる人が多いと思います。しかし、時空間を提案したのは、アインシュタインの師匠であるヘルマン・ミンコフスキーであり、1908年に発表された小論文である。ミンコフスキー空間の概念は、特殊相対性理論の本質である空間と時間を統一された全体の2つの側面として扱った最初のものである。彼は、この新しいアイデアが特殊相対性理論を明確にすることを期待していた。

ミンコフスキー時空は、等速性を表現するのにしか適していません。しかし、一般相対性理論で時空の曲率（重力）を発見したのは、アインシュタインでした。一般相対性理論では、アインシュタインはミンコフスキー時空を一般化し、加速度の影響を含めるようにしました。アインシュタインは、4次元の時空表現における曲率が、実は重力の原因であることを発見したのです。

1926年に出版されたブリタニカ百科事典の第13版には、アインシュタインの「時空」という記事が掲載されている。

文学的背景

エドガー・アラン・ポーが書いた『ユリイカ』（1848年）という宇宙論のエッセイには、「空間と時間は一つである」と書かれています。これは、空間と時間が一つのものに対する異なる認識であることを示唆した最初の例である。ポーは約90ページに及ぶ推論の末にこの結論を導き出したが、数学は一切用いていない。

1895年、H.G.ウェルズは小説『タイムマシン』の中で、「時間と空間の3つの次元との間には、我々の意識がそれに沿って動くということ以外に違いはない」と書いている。また、「科学者は、時間が空間の一種であることをよく知っている」とも述べている。

量子力学における時空

一般相対性理論では、時空は滑らかで連続していると考えられています。しかし、量子力学の理論では、時空は必ずしも連続的ではありません。

質問と回答

Q: テキストによると、時空とは何ですか?

A: 時空間とは、ミンコフスキー空間として知られる4次元の連続体を形成する、空間と時間をつなぐ数学的モデルです。

Q: 時空間の結合は宇宙論にどのように役立ちましたか。
A: 空間と時間を組み合わせることで、宇宙論は銀河のような大きなレベルから原子のような小さなレベルまで、宇宙がどのように機能しているかをよりよく理解できるようになりました。

Q: なぜ非相対論的古典力学では時空ではなくユークリッド空間を使うのがよいのですか?

A: 非相対論的古典力学において、ユークリッド空間を使うのがよいのは、時間が観測者の運動状態に依存せず、一定の速度で経過する普遍的なものとして扱われるからです。

Q: なぜ相対論的宇宙では時間は3次元空間と切り離せないのですか?

A: 相対論的宇宙では、時間は空間の3次元と切り離せません。なぜなら、観測される時間の経過速度は、観測者に対する物体の相対速度に依存するからです。

Q: 重力場の強さは物体の時間の経過にどのような影響を与えますか?

A: 重力場の強さは、場の外にいる観測者から見た物体の時間の流れを遅くします。

Q: 空間と時間をつなぐ4次元の連続体の名前は?

A: 空間と時間をつなぐ4次元の連続体はミンコフスキー空間と呼ばれています。

Q: 空間と時間の組み合わせは、宇宙論の理解にどのように役立ちましたか?

A: 空間と時間の組み合わせは、銀河のような大きなレベルから原子のような小さなレベルまで、宇宙の仕組みをより深く理解するのに役立っています。

百科事典を検索する