通常の最小二乗法
Ordinary least squares または Linear least squares は、統計学において未知のパラメータを推定する方法である。線形回帰で使用される手法である。この手法の目的は，観察された応答とデータの線形近似によって予測される応答との間の差を最小にすることである．差が小さいほど、そのモデルがデータによく適合していることを意味する。通常の最小二乗法は，一般に最小二乗法と呼ばれる手法の特殊なケースである．その結果得られる推定量は簡単な式で表すことができる。
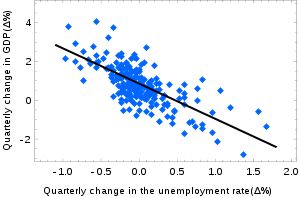
マクロ経済学におけるオクンの法則とは、ある経済においてGDP成長率は失業率の変化に直線的に依存するはずだというものである。ここでは、この法則を記述する回帰直線を作成するために、通常の最小二乗法が用いられている。観測値は青で、期待値は黒で示されている。
