平行ポスチュレート（ユークリッド第5公準）とは：定義と非ユークリッド幾何学への影響

幾何学において、平行ポスチュレートはユークリッド幾何学の公理の一つである。ユークリッドの『エレメント』の5番目のポスチュレートであることから、ユークリッドの5番目のポスチュレートとも呼ばれることがある。

もっと具体的には、古典的には次のように述べられることが多い：

線分を2本の直線で切ったとき、その直線が作る2つの内角の和が180°より小さい場合、その直線を長く伸ばせば、2つの直線は最終的に合流することになる。

定義と同値な表現

平行ポスチュレート（ユークリッド第5公準）は上のような幾何的記述のほかに、同等とされるいくつかの簡潔な表現がある。代表的なものは次の通りで、他のユークリッド的公理系を仮定すれば互いに同値である：

Playfair の公理：与えられた直線とその外の点について、その点を通り与えられた直線と交わらない直線は高々一つしか存在しない。
三角形の内角和が常に180°である、あるいは平行線に関する角の対応関係などを用いた形式。

歴史的経緯と独立性の発見

古代から18世紀までは、多くの数学者が第5公準は他の公理から証明できると考え、さまざまな試みがなされた。18〜19世紀にはヤーノシュ・ボヤイ、ニコライ・ロバチェフスキー（ロバチェフスキー幾何学）、およびカール・フリードリヒ・ガウスらが第5公準を仮定しない幾何学の研究を進め、ついに第5公準は他の公理からは導けない（独立である）ことが明らかになった。エウジェニオ・ベルトラミらの仕事により、非ユークリッド幾何がユークリッド幾何のモデルの中に一貫して構成できることが示され、相対的一貫性の理解が深まった。

非ユークリッド幾何学への影響

ユークリッドの公理にすべて従う幾何学の分野をユークリッド幾何学という。ユークリッドの公理にすべて従わない幾何学は、非ユークリッド幾何学と呼ばれる。

非ユークリッド幾何学は第5公準を否定することで生まれる主に二つのタイプがある：

双曲（ハイパーボリック）幾何学：ある直線と外部点について、その点からその直線に交わらない直線（いわゆる「平行」）が無数に存在する。三角形の内角和は180°より小さく、面積は内角和の欠損分に比例する。代表的なモデルにポアンカレ円板モデル、半平面モデル、クラインモデルなどがある。
楕円（あるいは球面）幾何学：どの二直線も交わる（平行線は存在しない）体系。球面上の大円は常に交わり、三角形の内角和は180°より大きくなる。

数学的・理論的な意味

第5公準の有無は「平行の一意性」「三角形の内角和」「図形の相似性」など基本的性質を決定する。例えば、ユークリッド幾何学では相似な三角形が多数存在するが、双曲幾何では相似だが合同でない三角形の性質が異なる。
第5公準が独立であることの発見は、幾何学が単一の絶対的な真理ではなく、公理系に依存する理論であることを示した。これが19世紀以降の数学の発展（抽象的公理化、代数的・位相的視点の導入）に大きく寄与した。
現代では、第5公準の代わりに〈平行性〉についての公理を置いたり、距離や曲率を直接導入して幾何学を定式化するなど、さまざまな公理系が使われている。

まとめ

平行ポスチュレート（ユークリッド第5公準）は、ユークリッド幾何学の核心的公理の一つであり、その可換性や独立性の問題は数学史に大きな足跡を残した。第5公準を置くか否かによって生じる幾何学の性質は大きく異なり、その研究は双曲幾何学・楕円幾何学といった新しい理論の誕生に直接つながった。

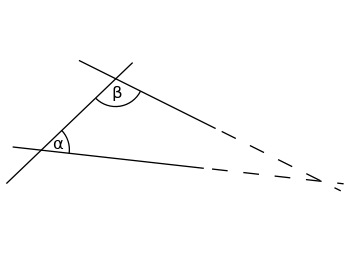
内角α（アルファ）とβ（ベータ）の和が180°より小さい場合、両者を無限大に延長すれば、2本の線はどこかで交わる。

歴史

数学者の中には、ユークリッドの第5仮定は他の4つの仮定よりずっと長く、複雑だと考えている人もいた。その多くは、他のもっと単純な公理から証明できると考えた。ある数学者は、より簡単な命題から証明したと発表したが、それらはすべて間違いであったことが判明した。

プレイフェアの公理

また、「プレイフェア公理」と呼ばれる最近の命題は、ユークリッドの第5ポスチュレートに似ている。それは次のようなものである。

ある直線とその直線上にない点があるとき、この点を通る直線でもう一方の直線にぶつからないものは1本しか引けません。

実は、この公理はユークリッドの第5仮定と似ているだけでなく、全く同じ意味合いを持っていることが数学者たちによって発見されたのである。数学的には、この2つの命題は「等価命題」と呼ばれる。今日、プレイフェア公理はユークリッドの原始平行ポスチュレートよりも頻繁に数学者に使用されている。

非ユークリッド幾何学

やがて、公理を用いずに新しい幾何学を構築しようとする数学者が現れた。非ユークリッド幾何学の一種に楕円幾何学がある。楕円幾何学では、平行ポスチュレートは、次のような公理に置き換えられる。

ある直線とその直線上にない点があるとき、この点を通り、最終的にもう一方の直線と交わらない直線は引けません。

数学者たちは、ユークリッドの第5仮定をこの公理に置き換えても、ユークリッドの他の多くの定理を証明できることを発見したのである。楕円幾何学をイメージする一つの方法として、地球儀の表面を思い浮かべることができる。地球儀では、赤道では経線が平行に見えるが、極点では経線がすべて交わる。19世紀後半になると、楕円幾何学が矛盾しないことが示された。これは、ユークリッドの第5仮定が他の仮定から独立していないことを証明するものであった。これ以降、数学者は他の4つの仮定から第5仮定を証明しようとすることをほとんどしなくなった。その代わりに、多くの数学者はユークリッドの第5約束に従わない他の幾何学を研究し始めた。

数学者は、ユークリッドの第5公理を別の公理で置き換えることがある。

ある直線とこの直線上にない点があるとき、この点を通り、最終的にもう一方の直線と交わらない直線を少なくとも2本引くことができる。

これを双曲線幾何学という。

もう一つの幾何学は、ユークリッドの第5仮定を単に取り除き、何にも置き換えないものである。これは中立幾何学または絶対幾何学と呼ばれる。