雪崩効果
雪崩効果（「地滑り効果」）は、ブロック暗号や暗号ハッシュ関数アルゴリズムの特性である。暗号ではよく望まれています。この効果は、入力が少ししか変化しない場合でも、出力の多くが変化しなければならないと言います。良いブロック暗号では、これは意味します。鍵や平文の小さな変化は、暗号文に強い変化をもたらすはずである。
これは、アルゴリズムが反復を使用する場合、小さな変更がすぐに広がることを意味します。したがって、出力のすべてのビットは入力のすべてのビットに依存します。
雪崩効果という用語は、最初にHorst Feistel（Feistel 1973）によって使用された。その後、この概念はシャノンの混同の性質によって同定された。
ブロック暗号や暗号ハッシュ関数が雪崩効果を有意に満たさない場合は、ランダム化が不十分である。したがって、暗号解析者は、出力だけを与えられれば、入力について予測を立てることができる。これは、アルゴリズムを部分的にまたは完全に破る（クラックする）のに十分であるかもしれない。
強力な暗号や暗号ハッシュ関数を作成する際の主な設計目的の一つです。彼らはその中に良い雪崩効果を構築しようとします。数学的にはこれはバタフライ効果を利用しています。これが、ほとんどのブロック暗号が製品暗号である理由です。また、ハッシュ関数が大きなデータブロックを持つ理由でもある。
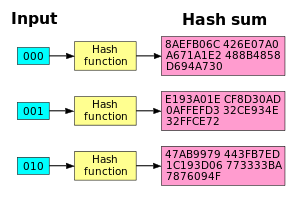
SHA1ハッシュ関数は雪崩効果が良い。1ビットを変更すると、ハッシュの和が全く違ったものになります。
名前
名前の由来は地すべりです。小さな岩が落ちてきて、いくつかの雪と一緒に進み、破壊的な地滑りを起こすことがあります。岩は小さかったが、多くの破壊を引き起こす可能性がある。これは、この効果が何をするかと同じです。インプット（岩）の小さな変化がアウトプット（景観）を変えるはずです。
厳格な雪崩基準
厳密雪崩基準(Strict Avalanche Criterion; SAC; "strong landslide criterion"と呼ばれる)は、ブール関数の特性です。これは暗号技術において重要です。入力ビットが1つ変更された場合、すべての出力ビットが50%の確率で変更された場合に満たされます。
SACは、進化の完全性とアバランシェの概念の上に構築された。これは1985年にWebsterとTavaresによって導入されました。今日では、すべての最新の暗号システムの要件となっています。例えば、AESコンペティションのファイナリスト全員がこの概念を満たしています。
ビット独立性基準
ビット独立性基準（BIC；ビットから独立した基準）は、基準である。となる。1つの入力ビットが変更（反転）されるとき、2つの出力ビットは互いに独立して変更されるべきである。これは、すべてのビットに適用される。
例えば、一方の出力ビットが変化するだけで、他方の出力ビットも変化する場合は満たされません。入力ビットが変化したために変化するだけかもしれません。そうでなければ、出力ビットは互いに依存しています。
関連ページ
- 混乱と拡散
質問と回答
Q:雪崩効果とは何ですか?
A:雪崩効果（「地滑り効果」とも呼ばれる）とは、ブロック暗号や暗号ハッシュ関数アルゴリズムの特性で、鍵や平文に小さな変化を与えると、暗号文に強い変化が生じるはずだとするものです。
Q:「アバランシェ効果」という言葉を最初に使ったのは誰ですか?
A:アバランシェ効果という言葉は、1973年にHorst Feistelが初めて使いました。
Q:シャノンの混信の性質とどう関係があるのですか?
A:ブロック暗号や暗号ハッシュ関数がこの度合いを相当程度満たさない場合、ランダム性が悪く、部分的または完全に破る（クラックする）ことができるというシャノンの混信の性質から、アバランシェ効果の概念が確認されました。
Q:強力な暗号を作るときの設計目的は?
A:強い暗号を作る場合、バタフライ効果などの数学的原理を利用して、雪崩効果をうまく作り込もうとします。ブロック暗号の多くがプロダクト暗号であるのも、ハッシュ関数が大きなデータブロックを持っているのもそのためです。
Q:アルゴリズムが雪崩効果を満たさない場合、どうなるのですか?
A:雪崩効果を満たさないアルゴリズムは、ランダム性に乏しく、与えられた出力のみから入力を予測できる暗号解読者により、部分的または完全に解読される可能性があるため、雪崩効果を満たすことができません。
Q:なぜブロック暗号の多くは積和音を使うのですか?
A: 多くのブロック暗号がプロダクト暗号を使用しているのは、バタフライ効果などの数学的原理を利用して、優れたアバラン ス効果をブロック暗号に組み込むのに役立つからです。
Q:なぜハッシュ関数は大きなデータブロックを持っているのですか?
A:ハッシュ関数が大きなデータブロックを持っているのは、バタフライ効果のような数学的原理を利用して、優れたアバランサ効果を構築するのに役立つからです。
