確率密度関数（PDF）とは？定義・性質・計算例でわかる入門

確率密度関数（PDF）の定義・性質を図解と計算例でやさしく解説。積分による確率の求め方まで丁寧に学べる入門ガイド。

確率密度関数とは、任意の連続確率分布に対して定義できる関数である。区間 [ a , b ] {\displaystyle [a,b]}における確率密度関数の積分は、与えられた密度を持つ与えられたランダム変数が与えられた区間に含まれる確率をもたらす。

確率密度関数は、連続分布を扱えるようになるために必要な関数である。サイコロを振ると、1から6までの数字が出て、確率は1 6 {\displaystyle {\tfrac {1}{6}}}となる。しかし、これは連続した関数ではなく、1から6までの数だけが可能なので、連続した関数ではありません。これに対して、2人の人の身長や体重は同じではありません。確率密度関数を使うと、180cm（71インチ）と181cm（71インチ）の間、または80kg（176.4ポンド）と81kg（178.6ポンド）の間の人の確率を決定することができますが、この2つの境界線の間には無限に多くの値が存在します。

定義と直感的な理解

確率密度関数 f(x) は、実数軸上の点 x に対して「その周辺に確率がどれだけ集中しているか」を表す関数です。ある区間 [a, b] にランダム変数 X が入る確率は

P(a ≤ X ≤ b) = ∫_a^b f(x) dx

で与えられます。ここで積分を取ることで、点ではなく区間に対する確率を得ます（連続分布では任意の1点の確率は 0 です）。

基本的な性質

• 非負性: f(x) ≥ 0 がすべての x について成り立ちます。
• 正規化: 全実数にわたる積分が 1 になる。つまり ∫_{−∞}^{∞} f(x) dx = 1。
• 累積分布関数（CDF）との関係: 累積分布関数 F(x) = P(X ≤ x) は F(x) = ∫_{−∞}^{x} f(t) dt で定義され、逆に連続な場合は f(x) = dF(x)/dx です。
• 値の大小についての注意: f(x) は確率そのものではなく密度なので、f(x) が 1 より大きくなることもあり得ます（例えば一様分布 on [0, 0.5] では f(x)=2）。重要なのは積分値が確率を表す点です。
• 単位: f(x) の単位は x の単位の逆数（例：身長が cm なら f の単位は 1/cm）です。

期待値と分散（代表値の計算）

確率密度関数を用いると期待値や分散を次のように定義できます。

• 期待値（平均）: E[X] = ∫_{−∞}^{∞} x f(x) dx
• 分散: Var(X) = E[(X − μ)^2] = ∫_{−∞}^{∞} (x − μ)^2 f(x) dx （ここで μ = E[X]）

代表的な確率密度関数の例

• 一様分布（区間 [a, b]）: f(x) = 1/(b − a) for x∈[a,b], それ以外は 0。任意の区間 [c,d]⊆[a,b] に入る確率は (d − c)/(b − a)。
• 正規分布（ガウス分布）: 平均 μ、標準偏差 σ の正規分布の密度は
  f(x) = (1 / (σ√(2π))) exp( − (x − μ)^2 / (2σ^2) )。多くの自然現象や測定誤差のモデルに用いられます。
• その他: 指数分布、ガンマ分布、ベータ分布など用途に応じてさまざまな連続分布があります。

具体的な計算例

例1 — 一様分布: 区間 [a, b] = [0, 10] の一様分布では f(x) = 1/10。0〜2 の間に入る確率は ∫_0^2 (1/10) dx = 2/10 = 0.2。

例2 — 正規分布（数値例）: 身長が平均 μ = 175 cm、標準偏差 σ = 5 cm の正規分布に従うと仮定する。170 cm から 180 cm の間に入る確率は標準化して z 値を使うと、

z1 = (170 − 175)/5 = −1, z2 = (180 − 175)/5 = 1

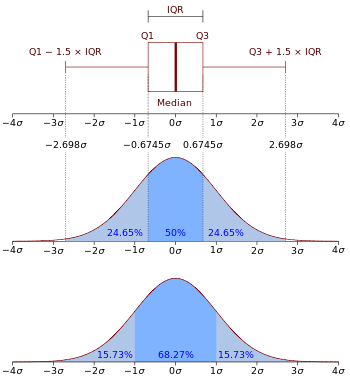
正規累積分布関数 Φ を使うと P(170 ≤ X ≤ 180) = Φ(1) − Φ(−1) ≈ 0.8413 − 0.1587 = 0.6826、つまり約 68.3% です（経験則の「平均±1σで約68%」と一致します）。

計算上の注意点

• 解析的に積分できない場合は数値積分（数値計算ライブラリや表）を使います。
• 境界を含むかどうか（≤ と <）は連続分布では確率に影響しませんが、定義上は一貫しておくとよいです。
• 確率質量関数（PMF）は離散分布に使い、確率密度関数（PDF）は連続分布に使うという区別を意識してください。

まとめ（実務的なポイント）

• PDF は「点での確率」ではなく「密度」を表す関数で、区間で積分することで確率を得る。
• f(x) は常に非負で、全体積（積分）は 1。
• 期待値や分散は f(x) を使って積分で計算できる。
• 値が 1 を超えることがあっても問題はなく、重要なのは積分結果である。

これらを踏まえると、確率密度関数は連続的な確率現象を扱うための基本的かつ強力な道具であることが分かります。

質問と回答

Q:確率密度関数とは何ですか?

Q:確率変数Xの確率密度関数はどのように書かれるのですか?

Q:確率密度関数の積分は何を表しますか?

Q:確率密度関数は、その領域全体で常に非負なのですか?

Q:区間を積分すると，和が1になりますか?

Q:確率密度関数は、どのような分布を特徴づけるのですか?

文字で検索