確率とは?定義と基礎をやさしく解説 — コイン・サイコロの例で学ぶ
コインやサイコロの例でやさしく学ぶ確率入門:定義から計算の基本まで、直感で理解できる解説と実例を掲載。
確率は応用数学の一部です。確率は偶然に起こる出来事(起こるかもしれないこと、起こらないかもしれないこと)を扱う学問で、何がどれくらいの「確からしさ」で起きるかを定量的に表します。
基本の用語
- 試行(experiment):観測や実験の一回の実行(例:コインを1回投げる)
- 結果(outcome):試行の一つひとつの可能な戻り値(例:表(ヘッド)か裏(テール))
- 標本空間(sample space):あり得るすべての結果の集合(例:サイコロなら{1,2,3,4,5,6})
- 事象(event):標本空間の部分集合。ある条件を満たす結果の集まり(例:「偶数が出る」など)
- 確率(P):ある事象が起こる度合いを0から1の数で表したもの。0は起こり得ない、1は確実に起こることを意味します。
身近な例:コインとサイコロ
例えば、コインを空中に投げて着地させると、片面が上を向くことを「表(ヘッド)」、反対を「裏(テール)」と呼びます。公正な(裏表が対称な)コインなら、表が出る確率は1/2、裏が出る確率も1/2です。
ダイス(複数:サイコロ)を振ると、1に着地する確率は1/6です。なぜなら、出る目は1, 2, 3, 4, 5, 6 の6通りで、どれも同じ確からしさ(公正なサイコロの仮定)だからです。1から6までのどれかが出る確率の合計は1になります(すべての可能性を合わせると必ず何かが起こるため)。
確率の計算でよく使うルール
確率の範囲:ある事象Aの確率P(A)は常に0 ≤ P(A) ≤ 1です。
加法の法則(排反事象):事象AとBが同時に起こらない(互いに排反)場合、 P(AまたはB) = P(A) + P(B)。 排反でない場合は重なり分を引いて P(AまたはB) = P(A) + P(B) − P(AかつB)。
乗法の法則(独立事象):事象AとBが互いに影響を及ぼさない(独立)とき、 P(AかつB) = P(A) × P(B)。 これは「二つのことが両方起こる確率は、それぞれの確率を掛け合わせる」と覚えるとよいです。
具体的な例と計算
- 2つのサイコロを同時に振って両方とも6が出る確率: 各サイコロで6が出る確率は1/6。独立なので P = (1/6)×(1/6) = 1/36 ≈ 0.02778(約2.78%)。
- サイコロを2回順に振って「1回目に3、2回目に5」が出る確率(順序を考える場合): P = (1/6)×(1/6) = 1/36 ≈ 0.02778。ここで「3と5のどちらかが出る(順序は問わない)」という事象なら、(3,5) と (5,3) の2通りがあり、確率は2/36 = 1/18 ≈ 0.05556(約5.56%)です。
- サイコロを3回振って「3、次に5、次に2」の順で出る確率: P = (1/6)^3 = 1/216 ≈ 0.00463(約0.463%)。これは元の文章にあった0.00463に対応します。
- 2個のサイコロの合計が10以上(つまり合計が10, 11, 12になる)になる確率: 全36通りのうち、合計10は3通り、11は2通り、12は1通りで合計6通り。したがって確率は6/36 = 1/6 ≈ 0.1667(約16.7%)。
計算の難しさと応用
単純なコインやサイコロの例は理解しやすいですが、現実問題では条件付き確率や組合せ、確率分布を使う必要があり、計算は複雑になります。例えば「6つのサイコロを振った場合、出目の合計が10以上になる確率」などは、単純な直感ではわかりにくいですが、数学的手法(組合せ、畳み込み、あるいはコンピュータでの列挙)を使って正確に求めることができます。
最後に:確率の直感
確率は、日常の不確実性を数量化する強力な道具です。以下を押さえておくと良いでしょう:
- 確率は0から1の数で表す(0=絶対に起こらない、1=必ず起こる)。
- 独立な事象の同時発生は確率を掛ける(乗法の法則)。
- 排反な事象の和は確率を足す(加法の法則)。
- 複雑な事象は、場合分けや組合せ、確率分布を使って分解すると計算しやすくなる。
確率はギャンブルだけでなく、統計、機械学習、物理学、保険、医療診断など幅広い分野で使われます。まずはコインやサイコロといった単純な例で感覚をつかみ、少しずつ条件付き確率や分布の考え方を学んでいくとよいでしょう。
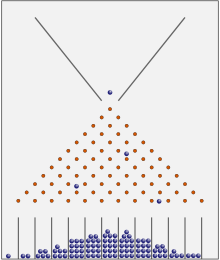
豆まき機やガルトンボックスでは,ほとんどのボールは中心に近いところで終わる.長い目で見ると,彼らは正規分布を示します.
確率のアイデア
ヤコブ・ベルヌーイ、ピエール・シモン・ラプラス、クリスティアン・ホイヘンスなどの人々は、上記のように確率という言葉を使っていました。他の人々は、周波数について考えた;確率の概念は、通常、周波数の確率と呼ばれています。
関連ページ
- 数学のトピック一覧
- 確率論
質問と回答
Q: 確率とは何ですか?
A:確率とは、応用数学の一部で、起こるかもしれないこと、起こらないかもしれないことを研究するものです。
Q: 確率はどのように表現できるのか?
A: 確率は、0(ありえない)から1(確実)の間の数値で表すことができます。
Q: 確率を使う例として、どのようなものがありますか?
A:確率を使った例としては、コインを空中に投げて着地させると、半分の確率で片面が上に、半分の確率でもう片面が上になることを示すことができます。
Q:2つのサイコロを振って、ある組み合わせが出る確率はどのように計算するのですか?
A:2つのサイコロを振って、ある組み合わせになる確率を計算するには、その2つの確率を掛け合わせます。例えば、3の次に5が出る確率を知りたい場合は、1/6×1/6=1/36となります。
Q: コインについて話すとき、「テイルズ」とは何を指すのでしょうか?
A:コインの場合、「テール」とは、顔や絵が描かれていない側を指します。
Q:サイコロを6個振って、10以上の数字が出る可能性はどれくらい?A:サイコロを6個振って10以上の数字が出る確率は、数学や科学で計算することができますが、自明なものではありません。
Q: 2つの確率を掛け合わせるとどうなるのか?
A: 2つの確率を掛け合わせると、両方のことが一度に起こる確率を計算することになります。
百科事典を検索する