確率空間
確率空間は、科学的な実験を記述するために使用される数学モデル 確率空間は、3つの部分から構成されています。
このように、このモデルでは、「モデルの実行結果」と「結果」の間には、「結果」と「結果」の間の関係があります。個々の結果はあまり実用的ではないかもしれないので、結果のグループを特徴づけるために、より複雑なイベントを使用します。そのような全ての事象の集合がσ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}}です。
.最後に、各イベントの発生可能性を指定する必要があります。これは確率測定関数Pを使用して行われます。
確率空間が確立されると、「自然」が動き出し、標本空間ωから一つの結果ωを選択すると仮定する。F の中で、選択された結果ωを含むすべての事象（各事象はωの部分集合であることに注意）を「発生した」とする。自然界で行われている選択は、実験を無限に繰り返すと、それぞれの事象の相対的な発生頻度が、関数 P で規定された確率と一致するように行われている。
ソ連の著名な数学者アンドレイ・コルモゴロフは、1930年代に他の確率の公理とともに確率空間の概念を導入しました。
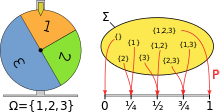
確率空間を用いた運勢の輪のモデル化
質問と回答
Q: 確率空間とは何ですか?
A: 確率空間とは、科学実験を記述するために使用される数学的モデルです。可能性のあるすべての結果を列挙した標本空間、0以上の結果を連想させる事象の集合、各事象に確率を割り当てる関数の3つの部分から構成される。
Q: 標本空間は何から構成されているのか?
A: 標本空間はすべての可能な結果からなり、Ω{displaystyle ˶ˆ꒳ˆ˵ ) と書かれることが多い。として、outcomeをω{displaystyle ˶ˆ꒳ˆ˵ ) .
Q:アウトカムとは何ですか?
A: 結果とは、モデルの1回の実行の結果です。
Q: 確率空間ではイベントは何に使われるのか?
A: 個々の結果は実用的でない場合が多いので、事象は結果のグループを特徴づけるために使われます。このようなイベントの集合をσ-algebraと呼び、F{displaystyle {mathcal {F}}と書くこともある。
Q: 各事象の確率はどのように割り振られるのか?
A: 確率測定関数Pを用いて各事象に確率を割り当てる。
Q: 確率空間の概念を導入したのは誰ですか?A: ソ連の著名な数学者であるアンドレイ・コルモゴロフが、1930年代に確率の公理とともに確率空間の概念を導入しました。
