ピタゴラスの定理とは：定義・公式（a^2+b^2=c^2）と証明・応用を解説

ピタゴラスの定理の定義・公式(a^2+b^2=c^2)を図解でわかりやすく解説。代表的な証明4分類と実践的な応用・例題まで、基礎から応用まで完全ガイド。

著者: Leandro Alegsa

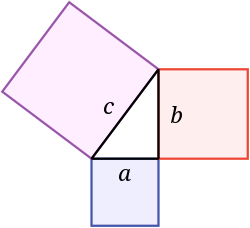
数学では、ピタゴラスの定理は、直角三角形の辺についての基本的で重要な定理です。直角三角形の直角をはさむ2辺を「脚」と呼び、直角に対する一番長い辺を「斜辺（しゃへん）」と呼びます。

直角三角形の角度の一つは、常に90度に等しい。この角度が直角です。直角の隣の2辺を脚と呼び、反対側の辺を次点と呼ぶ。次点は直角の反対側の辺で、常に一番長い辺です。

定義と公式

直角三角形で、脚の長さをa、もう一方の脚をb、斜辺の長さをcとすると、ピタゴラスの定理は次の等式で表されます。

a² + b² = c²

図形的には、斜辺の上に作った正方形の面積は、脚2辺の上に作った2つの正方形の面積の和に等しい、ということです。元々はギリシャの数学者ピタゴラスにちなんで名付けられていますが、この関係は古代メソポタミアやインドなどでも古くから知られていました。

{\displaystyle a^{2}+b^{2}=c^{2}}

証明の種類（代表例）

ピタゴラスの定理には数多くの証明が存在します。大まかに分類すると次の4つのタイプに分かれます。

  • 幾何学的証明：図形の面積を比較するもの（例：正方形の分割や合同図形を用いる方法）。ユークリッドの証明が有名です。
  • 代数的証明：座標を使って距離を計算する方法や方程式操作によるもの。
  • 等積変形や相似を使う証明：三角形の相似性を利用して辺の比から結論を得る方法。
  • 解析的・ベクトル的証明：内積・ベクトルノルムや三角関数を使う現代的な証明。

簡単な例

例えば脚が 3 と 4 の直角三角形では、斜辺 c は

c = √(3² + 4²) = √(9 + 16) = √25 = 5 となります。これがよく知られた「3-4-5」のピタゴラス数の例です。

ピタゴラス数（整数解）

a, b, c がすべて整数になるような直角三角形の辺の組 (a, b, c) をピタゴラス数（ピタゴラス三つ組）と呼びます。すべての原始的な（互いに素な）ピタゴラス三つ組は、整数 m > n > 0 に対して次の式で表されます：

  • a = m² − n²
  • b = 2mn
  • c = m² + n²

これに任意の正整数 k を掛けることで非原始な解も得られます（例：k(3,4,5））。

逆（合同）命題と一般化

ピタゴラスの定理の逆も成り立ちます。すなわち、三角形の辺の長さが a² + b² = c² を満たすなら、その三角形は直角三角形であり、斜辺は長さ c の辺です。これにより辺の長さから直角かどうかを判定できます。

また、ピタゴラスの定理はユークリッド平面における距離公式の特別形であり、余弦定理の特殊例（角が90度のとき）でもあります。余弦定理は任意の三角形に対して

c² = a² + b² − 2ab cos C

と表され、C = 90° のとき cos C = 0 となりピタゴラスの定理に一致します。さらに、ユークリッド空間のノルム（距離）概念により高次元にも一般化できます。

応用例

  • 測量・建築：直角の確認や斜辺の長さ計算。
  • 航法・地図作成：2次元平面での距離計算。
  • コンピュータグラフィックス・ゲーム開発：ピクセル間の距離、ベクトルの大きさ計算。
  • 三角法や解析学の基礎：三角関数や内積の性質の理解に必須。
  • 整数論：ピタゴラス数の研究は数論的関心を引きます。

歴史的な補足

この関係は紀元前のバビロニアやインドなどで独立に知られていた痕跡があり、定理の名は古代ギリシャの数学者ピタゴラスに由来します。誰が最初に証明したかは明確ではありませんが、ピタゴラス学派や後の数学者たちによって様々な証明が与えられ、広く普及しました。

まとめ

ピタゴラスの定理は、直角三角形におけるもっとも基本的な関係式 a² + b² = c² を与えます。直感的かつ多くの分野で使える道具であり、証明方法も多岐にわたるため、数学教育や応用数学の出発点として非常に重要です。

証明

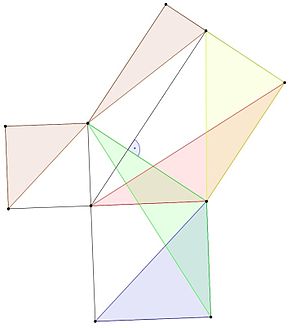
ピタゴラスの定理の一つの証明は、ギリシャの数学者、クニドゥスのエウドクサスによって発見されました。

証明には3つのリーマが使われています。

  1. 底面と高さが同じ三角形は、面積が同じです。
  2. 正方形の側面と同じ底辺と高さを持つ三角形は、正方形の半分と同じ面積を持ちます。
  3. 2つの面が合同で、1つの角が合同の三角形は、合同であり、同じ面積を持つ。

その証拠に

  1. 青色の三角形は、底辺と高さが同じなので、緑色の三角形と同じ面積を持っています（レモンマ1）。
  2. 緑と赤の三角形は、どちらも同じ正方形の辺に等しい2辺と、直線の角度（90度の角度）に三角形の角度を加えた角度を持っているので、一致しており、同じ面積を持っていることになります（レマ3）。
  3. 赤と黄色の三角形の面積は、高さと基底が同じなので等しい（レマ1）。
  4. 青色の三角形の面積は黄色の三角形の面積と同じなので

A b l l u e e = A g r e e n = A r e d = A y e l l o w {displaystyle {color {blue}A_{blue}}}={color {green}A_{green}}={color {red}A_{red}}={color {yellow}A_{yellow}}}}}}}}}}}}。 {\displaystyle {\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}}

  1. 茶色い三角形の部分は、同じ理由で同じ面積になっています。
  2. 青と茶色はそれぞれ小さい正方形の面積の半分を持っている。それぞれの面積の合計は、大きな正方形の面積の半分に等しい。このため、小さな正方形の面積の半分は、大きな正方形の面積の半分と同じなので、面積は大きな正方形の面積と同じになります。

似たような三角形を使った証明

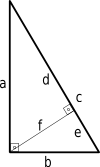
似たような三角形を使って、ピタゴラスの定理の別の証明を得ることができます。

d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}}quad ¶Rightarrow ¶quad d={\frac {a^{2}}{c}}quad (1)}. {\displaystyle {\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)}

e/b = b/c => e = b^2/c (2)

イメージから、c = d + e {displaystyle c=d+e,\!}{\displaystyle c=d+e\,\!}.そして、(1)式と(2)式を入れ替えることで

c = a 2 c + b 2 c { {\displaystyle c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}}

cの掛け算。

c 2 = a 2 + b 2 . {displaystyle c^{2}=a^{2}+b^{2},\!} {\displaystyle c^{2}=a^{2}+b^{2}\,\!.}

ピタゴラス三重

ピタゴラスの三つ子または三つ子は、3つの整数で、方程式a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}に適合します。{\displaystyle a^{2}+b^{2}=c^{2}}.

辺が３、４、５の三角形はよく知られた例である。a=3、b=4とすると、3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}}{\displaystyle 3^{2}+4^{2}=5^{2}} 9 + 16 = 25 {\displaystyle 9+16=25{\displaystyle 9+16=25}} となる。これは、３ ２＋４ ２＝５のようにもできる。{displaystyle {sqrt {3^{2}+4^{2}}}=5.} {\displaystyle {\sqrt {3^{2}+4^{2}}}=5.}

3-4-5の三角形は、3,4,5のすべての倍数に当てはまります。言い換えれば、6, 8, 10や30, 40, 50のような数字もピタゴラスの三角形である。三つ子のもう一つの例は、12-5-13の三角形で、12 2 + 5 2 = 13 {\displaystyle {sqrt {12^{2}+5^{2}}}=13} .{\displaystyle {\sqrt {12^{2}+5^{2}}}=13}

他の三重体の倍数ではないピタゴラスの三重体を原始ピタゴラスの三重体と呼ぶ。原始ピタゴラス三重は、式 ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})}を用いて求めることができる。{\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})}ただし、以下の条件を満たす必要がある。♪♪ ♪♪ ♪m♪ ♪n♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪

  1. m {pos(100,000)}mとn {pos(100,000)nは正の整数。
  2. m {\displaystyle m} mand n {displaystyle n} nhave no common factors except 1.
  3. ♪m {displaystyle m} mand n {displaystyle nn} have opposite parity. ♪m {displaystyle m} mand n {displaystyle n} nhave opposite parity when m {displaystyle m} mis even and n {displaystyle n} nis odd, or m {displaystyle m}m is odd and n {displaystyle n} is even. ♪m {displaystyle m} is odd and n {displaystyle n} nis even. ♪m {displaystyle m} and n {displaystyle n} have opposite parity when m {displaystyle m} is even.
  4. m > n {displaystyle m>n} .

4つの条件がすべて満たされるならば、m {displaystyle m}mとn {displaystyle nn}の値は、原始的なピタゴラスの3重になる。

m = 2 {\displaystyle m=2} {\displaystyle m=2}and n = 1 {\displaystyle n=1{\displaystyle n=1}} は、原始的なピタゴラスの三重項を作る。値は４つの条件をすべて満たす。2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2times 2\times 1=4}{\displaystyle 2mn=2\times 2\times 1=4}, m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3}and m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} {displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5}}。という{\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5}ことで、トリプル(3 , 4 , 5 ) {displaystyle (3,4,5)}が{\displaystyle (3,4,5)}作成されます。

質問と回答

Q:ピタゴラスの定理とは何ですか?


A:ピタゴラスの定理は、直角三角形の辺に関する記述である。

Q:直角三角形で常に90度になるのはどのような角度か?


A:直角三角形の角の1つは常に90度に等しく、これを直角と呼ぶ。

Q:直角の隣にある2つの辺は何と呼ばれているか?


A:直角の隣の2つの辺は脚と呼ばれる。

Q:直角の反対側の辺は何と呼ばれていますか?


A:直角の反対側の辺は斜辺と呼ばれ、常に最も長い辺である。

Q:この定理の計算式はあるのですか?


A:はい、「斜辺の長さの2乗は、他の2辺の長さの2乗の和に等しい」という定理を計算する方程式があります。

Q:90度の角度を持つ三角形はすべて「直角」三角形とみなされるのですか?


A: いいえ、90度の角度を持つ三角形はすべて「直角」三角形とみなされるわけではなく、一辺（斜辺）が他の二辺より長く、その端で90度の角度を形成するものだけが「直角」三角形として分類される。


百科事典を検索する
AlegsaOnline.com - 2020 / 2025 - License CC3