バンドギャップ（エネルギーギャップ）とは？定義・性質・半導体と絶縁体の違いを解説

バンドギャップ（エネルギーギャップ）の定義・性質を図解でわかりやすく解説。半導体と絶縁体の違いや電気伝導の仕組みを基礎から学べる入門ガイド

バンドギャップとは、固体内において電子状態が存在しないエネルギー範囲のことで、しばしばエネルギーギャップとも呼ばれます。これは固体物理学や化学の重要な概念で、物質の電気的性質を決める基本的な指標の一つです。バンドギャップは、典型的には絶縁体や半導体に見られ、価電子帯の上端と伝導帯の下端のエネルギー差（単位は電子ボルト（eV））として定義されます。すなわち、価電子帯に束縛されている電子が伝導帯に遷移して自由に動ける電荷キャリアになるために必要なエネルギー量です。実際には、外側の電子（外殻の電子が原子核の周りの軌道から解放される）ことで伝導が可能になります。

バンドギャップの物理的意味と単位

バンドギャップが示すのは、電子が物質中で利用できるエネルギー領域の「空白」です。値が大きいほど電子を伝導帯へ上げるエネルギーが必要になり、物質は電気を通しにくくなります。逆にバンドギャップが小さい、あるいは価電子帯と伝導帯が重なっている場合は、導体に近い振る舞いを示します。バンドギャップは通常eVで表現され、常温（約300 K）での電気伝導性や光吸収の波長域を決める重要なパラメータです。

直接ギャップと間接ギャップ

バンドギャップには主に二つのタイプがあります。直接バンドギャップでは、価電子帯の最大と伝導帯の最小が波数空間（k空間）で同じ位置にあり、光（光子）による電子の遷移が運動量をほとんど変えずに起こります。したがって光吸収や発光（LEDやレーザーに有利）が効率的です。一方、間接バンドギャップでは価電子帯と伝導帯の極大・極小が異なるk位置にあり、遷移にはフォノン（格子振動）を介した運動量のやり取りが必要で、光学的遷移が比較的低効率になります。

温度依存性とキャリア密度

バンドギャップは温度によってわずかに変化します（一般に温度上昇でギャップが小さくなる）。半導体では、固有のキャリア（電子と正孔）の生成率は概ね exp(−Eg/2kT) のように温度に敏感に依存し、Eg（バンドギャップ）が大きいほど常温での熱励起による自由キャリアは少なくなります。これにより、バンドギャップは材料の常温での導電性に直接影響します。

半導体と絶縁体の違い

• 絶縁体：バンドギャップが大きく（例えば数eV以上）、常温では電子の熱励起がほとんど起きないため電気伝導は非常に小さい。
• 半導体：バンドギャップが比較的小さく（例えば0.1〜3 eV程度）、温度やドーピング、光照射でキャリアを生成できるため、導電性を制御しやすい。これによりトランジスタやダイオードなどの電子デバイスに広く使われる。
• 導体：価電子帯と伝導帯が重なっているか、ギャップがほとんどないため自由電子が多く、電気をよく通す。

計測方法と実務上の扱い

バンドギャップの測定にはいくつかの方法があります。代表的なものは光吸収スペクトルや光励起（フォトルミネッセンス）測定、光電子分光（UPS/XPS）、電気伝導測定（温度依存測定）などです。光学的方法は光学ギャップ（光学的遷移の閾値）を、光電子分光は電子のエネルギー準位を直接調べるのに有効です。

材料設計と応用

半導体材料のバンドギャップは、ドーピング、合金化、ひずみ（ストレイン）、量子井戸・ナノ構造設計などで制御できます。バンドギャップの設計は多くの応用につながります：

• 発光ダイオード（LED）やレーザー：直接バンドギャップ材料が好まれる。
• 太陽電池：吸収できる光の波長域（バンドギャップ）により効率が左右される。
• 高耐圧・高周波デバイス：大きなバンドギャップ材料は高温・高電圧下で有利。
• センサー・フォトディテクタ：特定波長への感度をバンドギャップで調整。

代表的な材料例（参考値）

• シリコン（Si）：約1.12 eV（間接） — 一般的な電子デバイス用半導体
• ゲルマニウム（Ge）：約0.66 eV（間接）
• ガリウム砒素（GaAs）：約1.42 eV（直接） — 光デバイスに有利
• ダイヤモンド：約5.5 eV（直接に近く大きい） — 優れた絶縁体・高温材料

まとめ

バンドギャップは、電子の存在しないエネルギー領域であり、物質の電気伝導や光学特性を決定する重要な指標です。バンドギャップの大きさや性質（直接か間接か）は、材料の応用分野や性能に直結します。材料設計やデバイス開発では、バンドギャップを理解し適切に制御することが不可欠です。

半導体物理では

科学者は、バンドギャップを使って固体が電気を通すかどうかを予測する。ほとんどの電子（価電子と呼ばれる）は、1つの原子の原子核に引き付けられる。しかし、電子に十分なエネルギーがあり、最も近い原子核から飛び立つことができれば、固体を構成する多くの原子を横切る電流の流れに加わることができる。1つの原子核にぴったりとくっついていない電子は、伝導帯と呼ばれる。

半導体や絶縁体では、量子力学的に、電子はいくつかのエネルギーバンドにしか存在しないことがわかっている。電子は他のエネルギー準位に入ることを禁じられている。バンドギャップとは、価電子帯の上端と伝導帯の下端の間のエネルギー差のことである。電子は、あるバンドから別のバンドに飛び移ることができる。しかし、電子が価電子帯から伝導帯に移るためには、ある程度のエネルギーが必要である。必要なエネルギーの量は、物質によって異なる。電子は、フォノン（熱）やフォトン（光）を吸収することで、伝導帯に移るためのエネルギーを得ることができる。

半導体とは、バンドギャップが小さくゼロではない物質で、絶対零度（0K）では絶縁体として振る舞い、融点以下の温度では熱で電子が励起されて伝導帯に飛び込むことができる。反対に、バンドギャップが大きい物質は絶縁体となる。導体の場合、価電子帯と伝導帯が重なっていることがあるため、バンドギャップがない場合もある。

固有の半導体の伝導性は、バンドギャップに強く依存する。伝導に利用できるキャリアは、バンドギャップを越えて励起されるのに十分な熱エネルギーを持つ電子のみである。

バンドギャップエンジニアリングとは、GaAlAs、InGaAs、InAlAsなどの特定の半導体合金の組成を制御することで、材料のバンドギャップを制御・変化させるプロセスである。また、分子線エピタキシー法などにより、組成が交互に変化する層状の材料を作ることも可能である。これらの手法は、ヘテロ接合バイポーラトランジスタ（HBT）、レーザーダイオード、太陽電池などの設計に用いられている。

半導体と絶縁体の境界線を引くのは難しい。半導体はバンドギャップの狭い絶縁体の一種であると考えるのが一つの方法である。バンドギャップが大きい^絶縁体（通常3eV以上）^[?]は、半導体には含まれず、一般に実用的な条件下では半導体的な挙動を示さない。また、電子移動度は、半導体としての正式な分類を決定する上で重要な役割を果たす。

半導体のバンドギャップエネルギーは、温度の上昇とともに減少する傾向がある。温度が高くなると、原子の振動の振幅が大きくなり、原子間の間隔が大きくなります。また、格子フォノンと自由電子や正孔との相互作用もバンドギャップに少し影響を与える。バンドギャップエネルギーと温度の関係は、Varshniの経験式で説明できます。

E g ( T ) = E g 0( ) - α T T 2+ β {\displaystyle E_{g}(T)=E_{g}(0)-{\frac {\alpha T^{2}}{T+\beta }}}。ここで、E_g(0)、α、βは材料定数である。

通常の半導体結晶では、エネルギー状態が連続しているため、バンドギャップは固定されている。しかし、量子ドット結晶では、バンドギャップはサイズに依存し、価電子帯と伝導帯の間のエネルギー範囲を変化させることができる。これは量子閉じ込め効果とも呼ばれている。

また、バンドギャップは圧力にも依存する。バンドギャップには、電子バンド構造に応じて、直接的なものと間接的なものがあります。

数学的解釈

古典的には、エネルギー差ΔEのある2つの状態が電子に占有される確率の比をボルツマン係数といいます。

e ( - Δ E k T ) {displaystyle e^{\\left({frac {-᎑᎑᎑````E}{kT}}}}right)}}。

のところです。

• eはオイラー数（自然対数の底）。
• ΔEはエネルギー差
• kはボルツマン定数
• Tは温度。

フェルミ準位（または化学ポテンシャル）では、ある状態が占有される確率は1/2である。フェルミ準位が1eVのバンドギャップの中央にある場合、この確率は室温の熱エネルギー25.9meVでe⁻²⁰、約2.0⋅10⁻⁹となる。

太陽電池

電子は、光でも熱でも励起される。太陽電池が吸収する太陽光スペクトルの範囲は、バンドギャップによって決まる。発光型太陽電池は、発光媒体を用いて、バンドギャップ以上のエネルギーの光子を、太陽電池を構成する半導体のバンドギャップに近いエネルギーの光子にダウンコンバートする。

バンドギャップの一覧

素材	記号	バンドギャップ(eV) @ 302K	参考
シリコン	Si	1.11
セレン	セ	1.74
ゲルマニウム	Ge	0.67
炭化ケイ素	SiC	2.86
リン化アルミニウム	アルプ	2.45
アルミニウムアルセニド	AlAs	2.16
アルミニウムアンチモン	AlSb	1.6
窒化アルミニウム	AlN	6.3
ダイヤモンド	C	5.5
ガリウム(III)リン化物	GaP	2.26
ガリウム(III)ヒ素	GaAs	1.43
ガリウム(III)ナイトライド	GaN	3.4
硫化ガリウム(II)	GaS	2.5
ガリウムアンチモン	GaSb	0.7
アンチモン化インジウム	InSb	0.17
インジウム(III)ナイトライド	InN	0.7
リン化インジウム(III)	InP	1.35
インジウム(III)アルセニド	InAs	0.36
二珪化鉄	β-FeSi 2	0.87
酸化亜鉛	ZnO	3.37
硫化亜鉛	ZnS	3.6
セレン化亜鉛	ZnSe	2.7
テルル化亜鉛	ZnTe	2.25
硫化カドミウム	CdS	2.42
セレン化カドミウム	CdSe	1.73
テルル化カドミウム	CdTe	1.49
硫化鉛(II)	PbS	0.37
セレン化鉛(II)	PbSe	0.27
テルル化鉛(II)	PbTe	0.29
銅(II)酸化物	CuO	1.2
銅（I）の酸化物	2CuO	2.1

半導体のバンド構造。


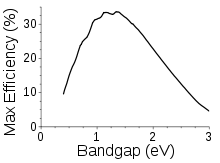
Shockley-Queisser限界は、半導体のバンドギャップの関数として、集中していない太陽光の下での単接合太陽電池の最大可能効率を示している。バンドギャップが高すぎると、ほとんどの太陽光線が吸収できず、低すぎると、ほとんどの太陽光線がバンドギャップを越えて電子を励起するのに必要なエネルギーよりもはるかに多くのエネルギーを持ち、残りは無駄になってしまう。商用の太陽電池に使われている半導体のバンドギャップは、シリコン（1.1eV）やCdTe（1.5eV）など、この曲線のピーク付近にある。ショックレー・キューサー限界は、タンデム型太陽電池や、太陽電池に太陽光を集中させるなどの方法で超えることができる。

質問と回答

Q:バンドギャップとは何ですか?

Q:固体物理学や化学では何を指す言葉なのですか?

Q:電気伝導性にどのような影響を与えるのですか?

Q:固体内で電子はどのように動いているのか?

Q:電子が高いエネルギーになるとどうなるのですか?

Q:固体はすべて絶縁体か半導体なのですか?

文字で検索