量子力学
量子力学（QM）は、原子よりも小さなレベルでの宇宙の仕組みを説明する学問です。量子物理学」や「量子論」とも呼ばれます。量子とはラテン語で「どれだけ」という意味であり、力学とは運動に関する科学の分野である。量子エネルギーとは、特定の量のエネルギーのことで、量子力学はそのエネルギーが原子レベルでどのように動き、相互作用するかを説明します。
かつて原子は、物質を構成する最小の単位と考えられていましたが、現代の科学では、陽子、中性子、電子など、さらに小さな粒子が存在することがわかっています。QMは、原子を構成する粒子の働きを説明する物理学の一部です。
量子力学は、光のような電磁波の仕組みについても説明しています。現代の物理学や化学の多くは、量子力学の数学的ルールを使って説明し、理解することができます。
素粒子や電磁波の研究に使われる数学は、非常に奇妙な動きをするため、非常に複雑です。
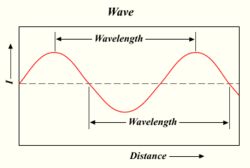
光の波の波長
波動と光子
光子は、原子や陽子、電子よりもはるかに小さい粒子で、実は質量を持っていません。光子は、エネルギーの「パケット」のようなものです。ロウソクやレーザーなどの光源は、光子と呼ばれる光のかけらを発射（放出）します。
光子の数が多ければ多いほど、ランプの光は明るくなる。光は、水の波やラジオの電波のようなエネルギーです。ある波の頂点から次の波の頂点までの距離を「波長」と呼びます。それぞれの光子は、その波長に応じて一定の量、すなわち「量子」のエネルギーを持っています。
光の色は、その波長によって決まる。バイオレット（虹の一番下の色）の波長は約400nm（ナノメートル）で、これは0.00004cmまたは0.000016インチに相当する。波長が10-400nmの光子は、紫外線（UV）と呼ばれる。このような光は人間の目では見ることができません。その反対に、波長が約700nmのものを赤色光と呼びます。赤外線は約700nm〜30万nm。人間の目は赤外光にも敏感ではない。
波長は必ずしも小さいわけではありません。電波にはもっと長い波長がある。FMラジオの波長は数メートルに及ぶこともある（例えば、99.5FMで送信している局は、約3メートル（約10フィート）の波長のラジオエネルギーを発している）。光子は、その波長に応じて一定のエネルギーを持っている。光子は、その波長に応じて一定のエネルギーを持っており、波長が短いほどエネルギーは大きくなる。例えば、紫外光は赤外光よりもエネルギーが大きい。
波長と周波数（1秒間に波が頂点に達する回数）は反比例しており、波長が長ければ周波数は低くなり、その逆もまた然りである。光の色が赤外線（赤い光よりも周波数が低い）の場合、それぞれの光子は当たったものを温めることができます。そのため、強い赤外線ランプ（ヒートランプ）を人に向けると、たくさんの光子にエネルギーが蓄えられているので、人は温かく感じ、あるいは熱くなります。赤外線ランプの表面が熱くなり、触った人が火傷することもある。人間は赤外線を見ることはできませんが、熱として感じることができます。例えば、太陽で暖められたレンガ造りの建物の前を通る人は、触らなくても建物の熱を感じることができます。
量子力学の数学的定式化は抽象的である。波動関数と呼ばれる数学的な関数は、粒子の位置や運動量などの物理的な性質の確率的な振幅（確率的な振幅の二乗が確率）に関する情報を提供する。量子力学の結果の多くは、古典力学の観点からは容易に可視化できない。
紫外光は紫外光よりも周波数が高く、可視光には含まれません。紫外線は、皮膚の細胞を傷つけ、日焼けを引き起こすほどの大きなエネルギーを持っています。実際、日焼けの多くは熱ではなく、太陽の紫外線の高いエネルギーが皮膚細胞を傷つけることで起こります。さらに高い周波数の光（電磁波）は、体の奥深くまで入り込み、より大きなダメージを与えます。X線はエネルギーが強いので、人体の奥深くまで入り込み、細胞を死滅させます。人間は、紫外線やX線を見たり感じたりすることはできません。人間は、紫外線やX線を見たり感じたりすることができないので、高周波の光を浴びたことに気づくのは、放射線による火傷をしたときくらいでしょう。細菌を死滅させることが重要な分野では、細菌や真菌などを死滅させるために紫外線ランプがよく使われます。X線は、がん細胞を殺すために使われることもあります。
量子力学は、「ある周波数はあるエネルギーを意味する」ということが発見されたことから始まった。エネルギーは周波数に比例します（E∝f）。周波数が高ければ高いほど、光子のエネルギーは大きくなり、ダメージも大きくなります。その後、量子力学は原子の内部構造を説明するようになった。また、光子が自分自身と干渉することなど、古典物理学では考えられなかったことも量子力学では説明できます。
左の黒は紫外線（高周波）、右の黒は赤外線（低周波）。
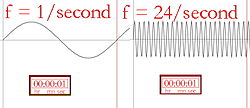
周波数の絵入り説明
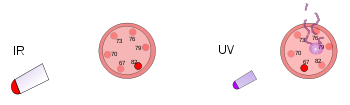
左の写真は、プラスチック製の温度計を明るいヒートランプの下に置いたもの。赤外線で温められていますが、温度計にダメージはありません。右の写真は、プラスチック製の温度計に低照度の紫外線を照射したもの。この放射線は、温度計を暖めることはないが、損傷を与える。
量子化
マックス・プランクは、周波数とエネルギーの関係を発見した。周波数とエネルギーが正比例する（つまり、どちらかが2倍になると、もう一方も2倍になる）ことは、それまで誰も考えていなかった。自然単位と呼ばれる単位の下では、光子の周波数を表す数値がエネルギーを表すことになります。そうすると、式は次のようになります。
E = f
つまり、エネルギーは周波数に等しい。
しかし、物理学の発展に伴い、エネルギーを測るための単位と、時間（つまり周波数）を測るための一般的な単位との間には、自然なつながりがなかった。そこで、プランクは、すべての数字を正しく表示するために、次のような式を考えた。
E = h × f
つまり、エネルギーはh×周波数になります。このhは、発見者の名前をとってプランク定数と呼ばれる数値です。
量子力学は、「ある周波数の光子は、あるエネルギーの光子を意味する」という知識に基づいています。その関係に加えて、特定の種類の原子は特定の周波数の放射線しか出すことができないので、一定のエネルギーを持つ光子しか出すことができません。
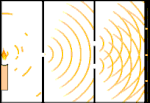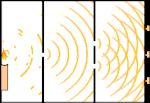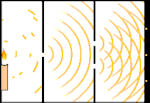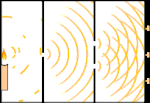
二重スリットの実験：光は左の光源から右のフリンジ（黒い縁でマークされている）へと向かう。
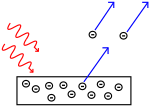
光電効果：光子が金属に当たり、電子が押し流される。
沿革
アイザック・ニュートンは、光は現在では粒子と呼ばれる非常に小さなものでできていると考えていました（彼はこれを「コーパスル」と呼んでいました）。ホイヘンスは、光は波でできていると考えていた。科学者たちは、粒子であると同時に波でもあることはできないと考えた。
科学者たちは、光が粒子でできているのか、それとも波でできているのかを調べるために実験を行いました。その結果、光は波でもあり粒子でもあるという、両方の考え方が正しいことがわかりました。トーマス・ヤングが行った二重スリット実験は、光が波のように振る舞う必要があることを示した。一方、アインシュタインが発見した光電効果は、光が特定のエネルギーを持った粒子のように振る舞い、そのエネルギーが周波数と関連していることを証明した。この実験結果は、量子力学における「波動と粒子の二重性」と呼ばれている。その後、物理学者たちは、光に限らず、あらゆるものが波のようにも粒子のようにも振る舞うことを発見しました。しかし、この効果は大きな物体ではずっと小さい。
量子力学の基本部分を発見した人たちを紹介します。マックス・プランク、アルバート・アインシュタイン、サテンドラ・ナート・ボース、ニールス・ボーア、ルイ・ド・ブロイ、マックス・ボルン、ポール・ディラック、ヴェルナー・ハイゼンベルク、ヴォルフガング・パウリ、エルヴィン・シュレーディンガー、ジョン・フォン・ノイマン、リチャード・ファインマン。彼らが活躍したのは20世紀前半のことである。
左から右へマックス・プランク、アルバート・アインシュタイン、ニールス・ボーア、ルイ・ド・ブロイ、マックス・ボルン、ポール・ディラック、ヴェルナー・ハイゼンベルク、ウォルフガング・パウリ、アーウィン・シュレーディンガー、リチャード・ファインマン。
プランクを超えて
光る水素から出る光を説明するために、量子力学の公式やアイデアが作られた。原子の量子論では、他の理論では説明できなかった、電子が軌道上に留まる理由も説明しなければならなかった。それまでの考え方では、電子は最初は自分のエネルギーで軌道を保っているが、軌道を回っているうちにすぐにエネルギーを失ってしまうので、原子の中心に落ちていかなければならないと考えられていた。(電子などの荷電粒子は、速度を変えたり回転したりすると光を発してエネルギーを失うことが知られていたからだ）。
水素ランプはネオンライトのように機能しますが、ネオンライトには独自の光の色（周波数）群があります。科学者たちは、光の色によってすべての元素を識別できることを知った。ただ、その周波数がどのようにして決まるのかが分からなかったのである。
そこで、スイスの数学者であるヨハン・バルマーが、λ（ラムダ、波の長さ）を表す方程式を導き出しました。
λ = B ( n n 224- ) n 456= , , {\\3lambda =B\left({frac {n^{2}}{n^{2}-4}}\right)\qquad ୨୧ n=3,4,5,6}。 
ここで、Bはバルマーが364.56nmに等しいと判断した数値です。
この式は、水素ランプの可視光に対してのみ有効であった。しかし、その後、この式はより一般的なものになりました。
1λ = R ( m 12-1 n ) , {\\lambda }}=R\left({1}{m^{2}}-{1}{n^{2}}}right2), }。 
ここで、Rはリュードベリ定数で、0.0110nmに等しく−1、nはmよりも大きくなければならない。
mとnに異なる数値を入れれば、多くの種類の光（紫外線、可視光線、赤外線）の周波数を簡単に予測することができます。この仕組みを知るには、ハイパーフィジックスにアクセスして、ページの中ほどを下っていきます。(水素はH=1としてください。)
1908年、ウォルター・リッツは、周波数間の特定のギャップが繰り返されることを示す「リッツ結合原理」を発表した。この原理は、数年後にヴェルナー・ハイゼンベルクにとって重要なものとなった。
1905年、アルバート・アインシュタインは、プランクのアイデアを用いて、光線が光子と呼ばれる粒子の流れで構成されていることを示した。各光子のエネルギーは、その周波数に依存する。アインシュタインの考えは、電子、陽子、中性子などのすべての素粒子が、波動であると同時に粒子でもあるという、量子力学の考え方の始まりです。(電子が波になっている原子の写真参照）これにより、波動粒子二重性という素粒子と電磁波に関する理論が生まれました。これは、粒子も波もどちらか一方ではなく、両方の性質を持っているというものです。
1913年、ニールス・ボーアは、「電子は原子核の周りに特定の軌道しか取れない」という考えを打ち出した。ボーアの理論では、上の式のmとnという数字は軌道を表すことができる。ボーアの理論では、電子はある軌道mに始まり、ある軌道nに終わるか、ある軌道nに始まり、ある軌道mに終わることができるので、光子が電子に当たるとそのエネルギーが吸収され、その余分なエネルギーのために電子はより高い軌道に移動することになります。ボーアの理論では、電子が高い軌道から低い軌道に落ちると、光子という形でエネルギーを放棄しなければならないことになる。光子のエネルギーは2つの軌道のエネルギー差に等しく、光子のエネルギーは特定の周波数と色を持っています。ボーアの理論は、素粒子現象の多くの側面をうまく説明していたが、光っている水素（および光っているネオンや他の元素）が発する光の色にはそれぞれ明るさがあり、その明るさの違いが元素ごとに常に同じである理由は答えられなかった。
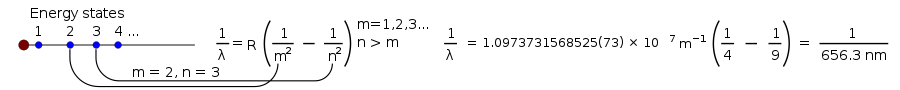
ニールス・ボーアが理論を発表した頃には、水素ランプの光に関するほとんどのことがわかっていたが、水素が光ることによって生じる各線の明るさについては、まだ説明がつかなかった。
ヴェルナー・ハイゼンベルクは、それぞれの線の明るさ、つまり「強度」を説明する仕事を引き受けた。バルマーが考えたような単純な法則は使えない。彼は、電子の質量（重さ）や電子の電荷（静電容量）などのわずかな量ですべてを計算する古典物理学の非常に難しい数学を使わなければならなかった。古典物理学では、水素ランプが出す色の帯の明るさについて、すでに答えが出ていましたが、古典理論では、4つの色の帯ではなく、連続した虹が出るはずだとしていました。ハイゼンベルグの説明は
光る水素が出す光の周波数には、何らかの法則があります。原子の核（中心）に近い軌道の間を電子が移動しているときには、周波数がばらばらになることを予測しなければなりませんが、軌道の間を電子が移動しているときの様子を見ていると、周波数がどんどん近くなることも予測しなければなりません。また、周波数間の強度差は、遠くに行くほど近くなることも予測しなければなりません。従来の物理学では、1つの方程式で正しい答えを出していましたが、新しい物理学では、同じ答えを異なる方程式で出さなければなりません。
古典物理学では、フランスの数学者フーリエの手法を用いて物理世界を数学的に表現しています。滑らかな曲線の集まりを使い、それらが一緒になって1つの滑らかな曲線を作り、この場合、ある光からすべての周波数の光の強さを与えます。しかし、この滑らかな曲線は高い周波数でしか現れないので、正しくありません。低い周波数では、常に孤立した点があり、点と点をつなぐものがありません。そこで、現実の世界の地図を作るために、ハイゼンベルクは大きな変化を起こさなければならなかった。自然界で見られるものと一致する数字だけを選び出すようなことをしなければならなかったのだ。この方程式を「推測した」と言われることがあるが、彼はやみくもに推測したわけではない。必要なものを見つけたのだ。彼が計算した数字は、グラフ上に点を置くことはできても、点と点の間に線は引かれません。計算のたびに点だけのグラフを作っていたのでは、紙の無駄遣いになってしまい、何もできなかった。ハイゼンベルクは、異なる周波数の強度を効率的に予測し、その情報を整理する方法を見つけたのです。
バルマーが始め、リドバーグが改良した経験則を使うだけで、ハイゼンベルグが望んでいた絵を描くのに役立つ1つの数値セットを得る方法がわかります。
このルールでは、電子がある軌道から別の軌道に移るとき、中心から遠くなるか近くなるかによって、エネルギーを得るか失うかが決まる。そこで、これらの軌道やエネルギー準位を、グリッドの上と横に沿って見出しとして入れることができます。歴史的な理由から、最も低い軌道をnと呼び、その次の軌道をn-a、次にn-bというように呼びます。実際には電子がエネルギーを得ているのに、負の数を使っているのは紛らわしいが、これは仕方のないことだ。
リュードベリの法則では周波数が得られるので、その法則を使って、電子がどこに行くかによって数字を入れることができます。電子がnから始まってnで終わるならば、電子はどこにも行っていないので、エネルギーを得ることも失うこともありません。もし、電子がn-aから始まってnで終わるなら、電子は高い軌道から低い軌道に落ちたことになり、そうすると周波数は0になります。そうすると、電子はエネルギーを失い、失ったエネルギーは光子として現れます。光子には一定のエネルギーeがあり、それはe=h fという式で一定の周波数fと関係しています。つまり、軌道が一定に変化すると、光の周波数fが一定になることがわかっています。電子がnから始まってn-aで終わると、低い軌道から高い軌道に移ったことになります。それは、ある周波数とエネルギーを持った光子が外から入ってきて、電子に吸収されてそのエネルギーを与えたときに初めて起こることで、それによって電子はより高い軌道に出て行くことになるのです。そこで、すべての意味を保つために、その周波数を負の数として書きます。ある周波数の光子があったのに、それが奪われてしまったのです。
ここで、f(a←b)は、電子がエネルギー状態（軌道）bからエネルギー状態aになるときの周波数を意味しています（配列が逆になっていますが、元々はそのように書かれています）。
fのグリッド
| 電子の状態 | n | n-a | N-B | n-c | .... | |
| f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | ||
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| N-B | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| transition.... | ..... | ..... | ..... | ..... |
ハイゼンベルクは、このようなグリッドを作ったわけではない。求めていた強度を得るための計算をしただけだ。しかし、そのためには2つの振幅（波の高さ）を掛け合わせて強度を算出しなければならない。(古典物理学では、強度は振幅の2乗に相当する）彼は、この問題を処理するために奇妙な式を作り、論文の続きを書いて上司に渡し、休暇に入ったのである。ボーン博士は、このおかしな方程式を見て、ちょっとおかしいなと思ったそうです。彼は、「なぜハイゼンベルグはこんな変なものをくれたのだろうか」と思ったに違いない。と思ったに違いない。そして、自分が見ているのは、自分がよく知っているものの設計図であることに気づいた。彼は、例えば周波数のためのすべての計算をして書ける格子や表を、行列と呼ぶことに慣れていた。そして、ハイゼンベルグの奇妙な方程式は、その2つを掛け合わせるためのルールだった。マックス・ボルンは非常に優秀な数学者でした。彼は、掛け合わされる2つの行列（格子）が異なるもの（例えば、位置（x,y,z）と運動量（mv）など）を表しているので、1つ目の行列に2つ目の行列を掛けると1つの答えが出て、2つ目の行列に1つ目の行列を掛けると別の答えが出ることを知っていたのです。行列計算を知らなかったハイゼンベルクは、この「答えが違う」という問題をすでに見ていて、悩んでいたのです。しかし、ボルン博士は優れた数学者で、1つ目の行列の掛け算と2つ目の行列の掛け算の違いには、プランク定数hに負の1の平方根iを掛けたものが必ず含まれることを見抜いていました。ハイゼンベルクが発見してから数日後には、ハイゼンベルクが好んで「不確定性原理」と呼んでいた基本的な数学がすでにできあがっていたのです。ハイゼンベルグの言う「不確定性」とは、電子のようなものは、固定されるまで固定されないという意味である。クラゲのように、常に押しつぶされていて、殺さない限り「一箇所」に留まることができないようなものだ。その後、「ハイゼンベルグの不確定性原理」と呼ばれるようになり、電子などは本当は「どこか」にあるのだが、自分の頭の中では不確定であると勘違いしている人が多くなった。その考えは間違っています。ハイゼンベルグの言っていることとは違うのです。測定ができないことは問題だが、それはハイゼンベルクが言っていた問題ではない。
ハイゼンベルクの考えは非常にわかりにくいものですが、例を挙げてわかりやすく説明します。まず、これらの格子を「行列」と呼ぶことにします。なぜなら、すぐに行列の乗算について話す必要があるからです。
位置(q)と運動量(p)の2種類の測定値がある状態からスタートしたとします。1925年、ハイゼンベルクはこのような式を書きました。
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\\ Y(n,n-b)=sum _{a}^{}\,p(n,n-a)q(n-a,n-b)}。(
共役変数である運動量と位置の式である。）
彼は知らなかったのですが、この方程式は、2つの行列（グリッド）を書き出し、それらを乗算するための青写真を与えてくれます。ある行列と別の行列を掛け合わせるためのルールは少し面倒ですが、ここでは設計図に従った2つの行列と、その積を紹介します。
pのマトリックス
| 電子の状態 | n-a | N-B | n-c | .... | |
| p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | ||
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| N-B | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| transition.... | ..... | ..... | ..... | ..... |
qのマトリックス
| 電子の状態 | N-B | n-c | N-D | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| N-B | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| transition.... | ..... | ..... | ..... | ..... |
ハイゼンベルグが1925年に発表した論文の関連式で指定されている、上記2つの行列の積の行列は
| 電子の状態 | N-B | n-c | N-D | ..... |
| A | ..... | ..... | ..... | |
| n-a | ..... | B | ..... | ..... |
| N-B | ..... | ..... | C | ..... |
どこで？
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....。
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....。
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....。
などと言っています。
このマトリックスを逆にすると、次のような値になります。
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
などと言っています。
掛け算の順序を変えると、実際に掛けられる数字が段階的に変わることに注目してください。
光る水素が放つ可視光。(波長はナノメートル。）
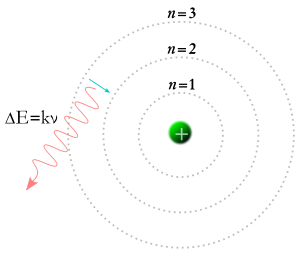
電子が下の軌道に落ち、光子が発生する。
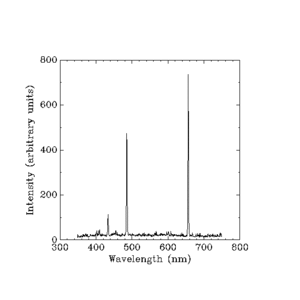
スペースアウトされた強度を任意の単位で
ハイゼンベルグを超えて
ヴェルナー・ハイゼンベルグの研究は、そのような状況を打破するかのように見えた。その後、ルイ・ド・ブロイ、マックス・ボルン、ポール・ディラック、ウォルフガング・パウリ、アーウィン・シュレーディンガーなど、さまざまな物理学者が、さまざまな方法で物事を説明するようになった。これらの物理学者の仕事は、それぞれが独自のストーリーを持っています。ハイゼンベルグをはじめとする初期の物理学者たちが使っていた数学は、それほど難しいものではありませんでしたが、原子の世界をより深く追求していくうちに、方程式は急速に複雑化していきました。
さらなるミステリー
量子力学が登場したばかりの頃、アルバート・アインシュタインは、もし量子力学が正しければ、「遠方での不気味な行動」が起こることになると示唆していました。しかし、結果的には量子力学は正しく、アインシュタインが量子力学を否定する理由としていたことが実際に起こったのです。このような量子現象の間の「不気味なつながり」は、現在では「量子もつれ」と呼ばれている。
実験によって2つのもの（光子、電子など）が集まったとき、それらは量子力学的に共通の記述をしなければなりません。後に分離しても、同じ量子力学的記述または「状態」を維持することができます。図では、一方の特性（例えば「アップ」スピン）が赤で、もう一方の特性（例えば「ダウン」スピン）が青で描かれています。紫の帯は、例えば2つの電子が一緒になったとき、そのペアが両方の特性を共有することを意味する。つまり、両方の電子がアップスピンかダウンスピンのどちらかを示すことになる。その後、2つの電子が分離され、1つは地球に残り、1つはケンタウルス座アルファ星のある惑星に行くと、それぞれの電子は両方のスピンを持っています。つまり、それぞれの電子は、スピンアップの電子とスピンダウンの電子のどちらを示すかを「決める」ことができるのだ。しかし、後で誰かがもう1つの電子を測定すると、その電子は逆のスピンを持っていることを「決定」しなければならない。
アインシュタインは、このような長距離で、一方の電子にスピンを強制的に与えて、もう一方の電子が反対の特性を示すようになると考えるのはおかしいと主張しました。彼は、2つの電子は最初からスピンアップまたはスピンダウンしていたはずだが、量子力学ではそれぞれの電子がどのような特性を持っているかを予測することができないと言った。予測できないということは、正しい実験でどちらか一方しか見ることができないということであり、量子力学は何か重要なことを説明できないということになる。そのため、アインシュタインは「量子力学には大きな穴が開いている」と言いました。量子力学は不完全なのです。
その後、実験の結果、間違っていたのはアインシュタインだったことが判明しました。
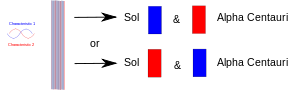
もつれた2つの粒子が分離されます。1つは地球上にあり、もう1つはどこか遠くの惑星に運ばれます。一方の粒子を測定すると、どちらの役割を担うかを強制的に「決定」させられ、もう一方の粒子は、その後、測定されるたびに、もう一方の役割を担わなければならなくなります。
ハイゼンベルグ不確定性原理
1925年、ヴェルナー・ハイゼンベルクは「不確定性原理」を発表しました。これは、ある粒子がどこにあるかを知れば知るほど、その粒子がどのくらいの速さでどの方向に進んでいるかを知ることができなくなるというものです。言い換えれば、小さなものの速度と方向がわかればわかるほど、その位置はわからなくなるということです。物理学者は通常、このような議論では速度の代わりに運動量のことを話します。運動量とは、ある方向への速度に質量をかけたものです。
ハイゼンベルグの不確定性原理とは、ある粒子の位置と運動量の両方を知ることはできないというものです。光は豊富な粒子であるため、他の粒子を測定するために使われます。測定するには、光の波を粒子に跳ね返して、その結果を記録するしかありません。高エネルギー、つまり高い周波数の光を使えば、どこにあるかは正確にわかりますが、どれくらいの速さで進んでいたかはわかりません。これは、高エネルギーの光子が粒子にエネルギーを与え、粒子の速度を変えるためです。一方、エネルギーの低い光を使うと、粒子の速さはわかりますが、どこにいるかはわかりません。これは、波長の長い光を使っているからです。波長が長いということは、粒子が波の延長線上のどこにでもある可能性があるということです。
また、この原理では、どんなに努力しても、ある粒子（非常に小さなもの）について両方の測定値を知ることができない測定値のペアが多く存在するとしています。そのようなペアの一方について知れば知るほど、もう一方については知ることができなくなるのです。
アインシュタインも、このような奇妙な概念を受け入れることができず、「神はサイコロを振らない」と言ったことは有名な議論である。これに対し、デンマークの物理学者ニールス・ボーアが「アインシュタインよ、神に何をすべきか言うな」と答えたのは有名な話だ。
QMの用途
原子の核の周りには電子があります。化学結合は原子をつなぎ、分子を形成する。化学結合は、2つの原子の間で電子が共有されることで、2つの原子を結びつけます。このように、QMは化学結合の物理学であり、化学の物理学でもあるのです。QMは、分子がどのように作られ、どのような性質を持つのかを理解するのに役立ちます。
QMは、星や宇宙全体などの大きなものを理解するのにも役立ちます。QMは、ビッグバンと呼ばれる宇宙の始まりの理論の非常に重要な部分です。
物質でできているものは、重力という基本的な力によって、他の物質に引き寄せられます。重力を説明するアインシュタインの理論は、一般相対性理論と呼ばれています。現代物理学の問題点は、QMの結論が一般相対性理論と一致していないように見えることです。
QMは、すべての電子技術がそのように機能する理由を説明できる物理学の一部です。コンピュータが電子機械である以上、QMはコンピュータの動作を説明することができます。しかし、1950年や1960年頃の初期のコンピュータハードウェアの設計者は、QMについて考える必要はありませんでした。また、当時のラジオやテレビの設計者もQMを考えていませんでした。しかし、近年のより高性能な集積回路やコンピュータのメモリ技術の設計にはQMが必要です。
QMは、以下のような技術も可能にしました。
QMを学ぶのが難しい理由
QMは、いくつかの理由で挑戦的なテーマです。
- QMは、私たちが子供の頃に世界について学んだこととは全く異なる方法で物事を説明します。
- QMを理解するには、代数や単純な微積分よりも多くの数学が必要です。また、行列代数、複素数、確率論、偏微分方程式なども必要です。
- 物理学者たちは、QMの方程式のいくつかが現実の世界について何を語っているのかよくわかっていません。
- QMは、原子や素粒子が日常生活とは全く異なる不思議な振る舞いをすることを示している。
- QMは非常に小さいものを記述するので、特別な装置がないと見えないものもあれば、全く見えないものもあります。
QMは、通常の科学の考え方とは異なる方法で自然を記述します。QMは、ある物事が確実に起こると言うのではなく、どれくらい起こり得るかを教えてくれます。
その一例がヤングの二重スリット実験である。一枚の写真フィルムにレーザーから単一の光子（一単位の光）を照射すると、現像されたフィルムには一点の光が見える。その間に金属板を置いて、非常に狭いスリットを2つ作り、金属板にたくさんの光子を発射して、その光子がスリットを通過するようにすると、驚くべきことが起こります。現像されたフィルムのシート全体に、明暗の帯が連続しているのが見えます。明るい帯がどこにあるか、その帯を作った光の明るさはどれくらいだったか、つまり、それぞれの帯にどれだけの光子が降り注ぐかを、数学を使って事前に知ることができるのです。しかし、プロセスを遅くして、それぞれの光子がスクリーンのどこに落ちるかを見ても、次の光子がどこに現れるかを前もって知ることはできません。光子が中央の明るいバンドに当たる可能性が最も高く、中央から遠く離れたバンドに光子が現れる可能性はだんだん低くなっていくことは確実にわかります。つまり、バンドが中心で最も明るく、遠くなるほど暗くなることは確実に分かっています。しかし、どの光子がどのバンドに入るのかは、はっきりとはわかりません。
QM理論の奇妙な結論の一つに「シュレーディンガーの猫」効果があります。粒子の位置、運動速度、運動方向、「スピン」などの特性は、何かがそれを測定しないと語ることができない（例えば、光子が電子に跳ね返ってきたら、その位置を測定したことになる）。測定前の粒子は、その特性が同時に多くの値を持つ「状態の重ね合わせ」にある。シュレーディンガーは、「量子力学は、何か（猫の生死など）が量子的な事象によって決定される場合、その状態は量子的な事象の結果としての状態によって決定されるが、それは誰かが量子的な事象の状態を見た時に限られる」と言っているようだと述べた。量子事象の状態を見る前の時間には、おそらく「生きている猫と死んでいる猫（失礼）が同じくらいの割合で混ざっているか、まみれている」のではないでしょうか。
縮小プランク定数
よく使われるのが、記号「ℏ」です。
これは "h-bar "と呼ばれています。ℏ = h π2 {\\hbar ={frac {h}{2\pi }}} 。
H-barは角運動量を表す単位である。この新しい単位を使って原子の電子の軌道を記述すると、軌道上の電子の角運動量は常に整数になる。
例
1次元の井戸の中の粒子は、粒子のエネルギーが特定の値しか持たないことを示す最も単純な例です。このエネルギーは "量子化されている "と言われます。井戸は、ある範囲内ではゼロの位置エネルギーを持ち、その範囲外では無限の位置エネルギーを持つ。x方向に1次元の場合
、時間に依存しないシュレーディンガー方程式は次のように書ける。
- 2ℏ2 m d 2ψ d x =2 E ψ .{E\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\amatsuamatsuamatsuamatsuamatsuamatsuamatsuamatsuamatsuamatsuamatsuamatsuamatsuamatsu.} 
微分方程式を用いると、ψ{\\}
は、次のようになります。
ψ = A e i k x + B e - i k x E = ℏ2 k m22 {\\\\\ = Ae^{ikx}+Be^{-ikx}\;\;E={\\\\}}。 
または
ψ = C sin k x + D cos k x {\\sin kx+D\cos kx\; }。
(by オイラーの公式)
箱の壁があるということは、波動関数が特別な形をしていなければならないということです。壁が無限に高くても、粒子の波動関数はゼロでなければなりません。それぞれの壁で
ψ = a0 t x = ,0 x = L ψ = a t x = , x = L ψ = a t x = , x = L ψ = a t x = 0, ψ = a t x = 0, ψ = a t x = L 
x = 0を考える
- sin 0 = 0, cos 0 = 1となる。ψ = {\\\\\\\\\\\\0⁾⁾
を満たすためには、cos項を削除しなければならない。したがって、D = 0
ここで考えてみましょう。ψ = C sin k x {\\\\ = Csin kx˶｝ 
- at x = L, ψ = C sin k L = {\\0 sin kL=0\; }.
- C = 0 ならば、ψ = {0displaystyle ˶‾᷄ -̫ ‾᷅˵} for all x. この解は役に立たない。
- したがって、sin kL = 0が成り立つことになり、次のようになります。
k L = n π n 24= , , , , ... .135{n=1,2,3,4,5,......であることを表しています。｝ 
nは整数でなけれ
ばならないことがわかります。これは、粒子が特別なエネルギー値しか持たず、その間のエネルギー値を持つことができないことを意味する。これがエネルギーの "量子化 "の例である。
関連ページ
- 電磁波
- 電子
- フォトン
- 量子もつれ
- Schrödinger方程式
質問と回答
Q: 量子力学とは何ですか?
A: 量子力学は、原子よりも小さなスケールで宇宙がどのように機能しているかを説明する物理学の一分野です。量子物理学、量子論とも呼ばれます。
Q:「量子」という言葉はどういう意味ですか?
A:「量子」という言葉はラテン語から来ており、「どれだけの」という意味です。量子力学では、エネルギーがどのように動き、どのように相互作用するかを記述します。
Q:素粒子とは何ですか?
A:素粒子とは、陽子、中性子、電子など、原子を構成する粒子のことです。原子よりもさらに小さい粒子です。
Q: 量子力学は素粒子の働きをどのように説明しているのですか?
A:量子力学は、素粒子や電磁波の振る舞いや相互作用を理解するための数学的ルールを提供します。
Q:波動粒子二重性とは何ですか?
A:波と粒子の二重性とは、粒子と波が互いに似たような振る舞いをすることで、2つの異なる存在ではなく、両者が結合して1つの現象になったようなものです。
Q:量子力学を使うと、現代物理学はどのように記述できるのですか?
A:現代の物理学や化学は、量子力学の数学的ルールを適用することによって説明することができます。
