宇宙の形
宇宙の形状は、すべての用語がアインシュタイン相対性理論のものでなければならないので、日常的な用語で議論することはできません。したがって、宇宙の幾何学は、私たちの日常生活の中にある普通のユークリッド幾何学ではありません。
特殊相対性理論によれば、二つの異なる事象が同時に発生するかどうかは、その事象が空間的に分離されている場合には判断できない。宇宙の形（ある時点での）」を語ることは、特殊相対性理論の観点からはナイーブである。同時性の相対性のために、空間の異なる点を「同じ点にある」とは言えないし、「ある点にある宇宙の形」とも言えない。
天体物理学者が行うことは、宇宙の特定のモデルが、宇宙の観測や測定によって知られていることと一致しているかどうかを問うことです。もし観測可能な宇宙が全宇宙よりも小さい場合（モデルによっては何桁も小さい、あるいは無限小である場合もある）、観測は全体の一部に限定されます。
宇宙の形を考えることは、2つに分けることができます。
- 局所幾何学
- 大域幾何学は、宇宙全体のトポロジーに関連するもので、測定が不可能な場合があります。
観測可能な宇宙は、宇宙のあらゆるモデルを検証するための基礎となるものである。それは、宇宙全体の形に関係なく、観測者を中心とした球状の体積（ボール）です。宇宙のあらゆる場所には、地球を中心とした観測可能な宇宙があり、それと重なっている場合もあれば、重なっていない場合もあります。
最近の測定では、NASAが「宇宙は0.4％の誤差しかないフラットな状態であることがわかった」と発表しています。モデルの一つであるFLRWモデルの中で、現在最も人気のある宇宙の形状は、観測データに適合することがわかっている無限フラットモデルです。他にもデータにフィットするモデルがあります。
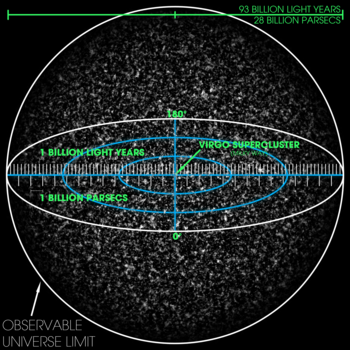
930億光年（280億パーセク）の3次元観測可能な宇宙の可視化。微細な粒が多数のスーパークラスターの集合体を表している。天の川の本拠地である乙女座スーパークラスターは中央にあるが、小さすぎて画像には写っていない。
質問と回答
Q:現在の観測では、宇宙の形はどうなっているのでしょうか?
A: 最近の測定によると、NASAは、0.4%の誤差で宇宙は平らであると述べています。
Q: 特殊相対性理論は、宇宙の形についての理解にどのような影響を与えるのでしょうか?
A: 同時性の相対性理論により、2つの異なる事象が空間的に離れている場合、その事象が同時に起こるかどうかを判断することはできません。つまり、空間上の異なる点が「同じ時刻にある」と言うことはできず、「ある時刻の宇宙の形」を語ることはできない。
Q: 宇宙物理学者が宇宙の形状を議論するとき、どのような幾何学を使うのでしょうか?
A: 宇宙物理学者は、宇宙を記述し予測するためのモデルを議論し検証する際に、アインシュタイン相対性理論を使用します。また、特に曲率に関係する局所幾何学とトポロジーに関係する大域幾何学も考慮します。
Q: 宇宙のすべての場所は、観測可能な宇宙の一部なのですか?
A: はい、宇宙のすべての場所は、地球を中心とした宇宙と重なることもあれば重ならないこともある、独自の観測可能な宇宙を持っています。
Q: 宇宙を記述・予測するためのモデルで、「平坦」とはどういう意味ですか?
A: FLRW（Friedmann-Lemaître-Robertson-Walker） と呼ばれるモデルの中で、「平坦」とは、観測データに最も適合するとされる無限平面モデルのことを指します。このモデルでは、空間はどこを見ても一様に見え、曲線や屈曲は存在しないのです。
Q: FLRWの無限平面モデル以外に、観測データに合うモデルはあるのでしょうか?
A: はい、FLRWの無限平面モデル以外にも、観測データに適合するモデルがあります。
