フーリエ級数
ジョセフ・フーリエは、正弦波を使って別の関数を近似することが可能であると述べた。これは数学的な意味での級数です。この理論はフーリエ変換に一般化できます。これらの関数を数学的に解析することをフーリエ解析といいます。
18世紀には、オイラー、ラグランジュ、ベルヌーイなどの数学者が、すでに正弦波を使って他の関数の近似やモデル化を行っていました。1822年にフーリエが熱に関する研究を発表したとき、フーリエはこのような関数（区間で連続しているもの）には、このような近似が存在すると言いました。最初は人々に信じてもらえず、（問題の一部を）証明するものが登場するまでに10年近くかかった。
現在、フーリエ級数はデジタル信号処理に多く用いられています。
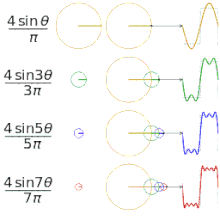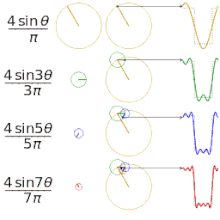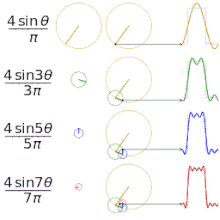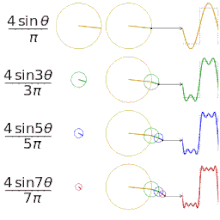
フーリエ級数を用いて異なる正方形関数を近似する
質問と回答
Q: ジョセフ・フーリエとは誰ですか?
A: ジョセフ・フーリエはフランスの数学者で、正弦波を使って別の関数を近似できることを提唱しました。
Q: フーリエ級数とは何ですか?
A: フーリエ級数とは、正弦波を使って別の関数を近似する級数のことです。
Q: フーリエ変換とは何ですか?
A: フーリエ変換とは、正弦波を使って別の関数を近似する理論の一般化です。
Q: フーリエ解析とは何ですか?
A: フーリエ解析とは、正弦波を使って別の関数を近似する関数の数学的解析です。
Q: 18世紀に正弦波を使って他の関数を近似し、モデル化したのは誰ですか?
A: オイラー、ラグランジュ、ベルヌーイなどの数学者が18世紀に正弦波を使って他の関数を近似し、モデル化しました。
Q: フーリエは1822年の熱に関する研究で何を提案しましたか?
A: フーリエは1822年の熱の研究で、正弦波を使った近似が、与えられた区間内のどんな連続関数に対しても存在することを提案しました。
Q: ディジタル信号処理におけるフーリエ級数の使い方とは?
A: フーリエ級数は、デジタル信号処理において、信号の近似や解析に多用されます。
