フーリエ変換

フーリエ変換は、信号や波を構成する基本周波数を見つけるために使用できる数学関数です。例えば、和音が演奏されている場合、和音の音波をフーリエ変換に入力して、その和音がどの音からできているかを見つけることができます。フーリエ変換の出力は、入力された周波数のスペクトルを表示するため、周波数スペクトルや分布と呼ばれることもあります。この関数は、暗号学、海洋学、機械学習、放射線学、量子物理学のほか、サウンドデザインや可視化にも多くの用途があります。

関数f ( x )のフーリエ変換は次のように与えられる f(x) 。

F ( α ) = ∫ - ∞ + ∞ f (x ) e - 2 π i α x d x {displaystyle F(\alpha ) = ∫ - ∞ + ∞ f (x ) e - 2 π i α x d x {displaystyle F(\alpha ) = ™ ™ ™ ™ ™ F(x)e^{-2π i\alpha x}d x} $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx$

αは周波数だ $\alpha$ よ

F ( α ) {displaystyle F(\alpha )}は $F(\alpha )$ 、フーリエ変換関数であり、元の信号の中にどれだけ有病率の高い周波数α {\displaystyle \alpha $\alpha$ }があるかを表す値を返す。

e - 2 π i α x {displaystyle e^{-2π i\alpha x}}}}}。 $e^{-2\pi i\alpha x}$ 入力関数 f ( x ) {\displaystyle f(x)}を複素平面内の原点の周りに、 f(x) いくつかの周波数で包み込むことを表す。 $\alpha$

逆フーリエ変換は次式で与えられます。

f (x ) = ∫ - ∞ + ∞ F (α ) e + 2 π i x α d α {displaystyle f(x)=\infty }^{+\infty }F(α )e^{+2\i i xα }d\alpha } $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha$

フーリエ変換は、信号にどのような周波数が含まれているかを示します。例えば、3つの異なる音符を含む音波を考えてみましょう。この音波のフーリエ変換のグラフを作成すると（周波数をx軸に、強度をy軸に）、音符の1つに対応する各周波数にピークが表示されます。

振幅と周波数の異なる余弦と正弦を足し合わせることで、多くの信号を作成することができます。フーリエ変換は、これらの余弦と正弦の振幅と位相をそれぞれの周波数に対してプロットします。

フーリエ変換は、周波数が分離されていると多くの信号がより意味を成すので重要です。上のオーディオの例では、時間を基準に信号を見ても、音符A、B、Cが信号の中にあることは明らかではありません。多くのシステムは、異なる周波数に対して異なることを行うので、この種のシステムは、それぞれの周波数に対して何を行うかによって説明することができます。その例として、高音域をブロックするフィルターがあります。

フーリエ変換を計算するには，積分と虚数の理解が必要です．コンピュータは通常、最も単純な信号以外のあらゆるもののフーリエ変換を計算するために使用されます。高速フーリエ変換は、コンピュータがフーリエ変換を素早く計算するために使用する方法です。

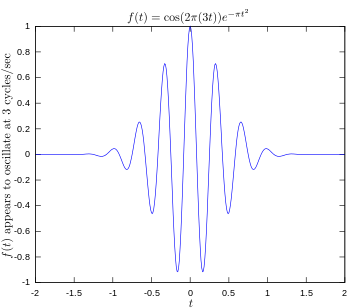
3ヘルツで発振している信号を示すオリジナル関数。

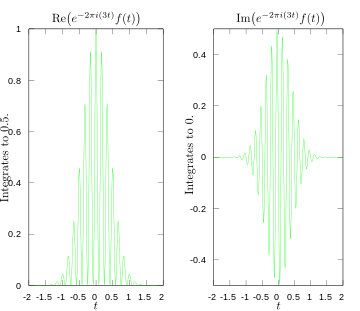
3ヘルツでのフーリエ変換の積分器の実部と虚部

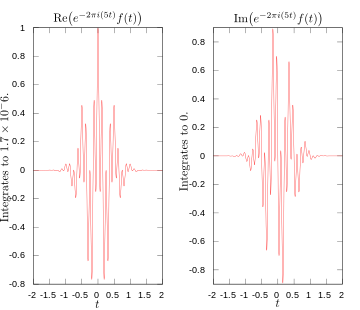
5ヘルツでのフーリエ変換の積分器の実部と虚部

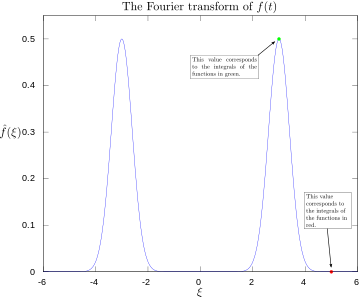
3ヘルツと5ヘルツをラベル化したフーリエ変換。

質問と回答

Q:フーリエ変換とは何ですか?

A:フーリエ変換とは、波が構成する基本周波数を求めるために使用できる数学関数です。複雑な波からそれを構成する周波数を求め、和音を構成する音を特定することができます。

Q:フーリエ変換にはどのような使い道があるのでしょうか?

A:フーリエ変換は、暗号学、海洋学、機械学習、放射線学、量子物理学のほか、音響設計や可視化など、多くの用途に使われています。

Q:フーリエ変換はどのように計算するのですか?

A:関数f(x)のフーリエ変換は、F(ב) = ∫-∞+∞f(x)e-2נiבxdx （בは周波数）で与えられます。これは、周波数בが元の信号の中でどれだけ優勢であるかを表す値を返す。逆フーリエ変換は、f(x) = ∫-∞+∞F(ב)e+2נixבdב で与えられます。

Q:フーリエ変換の出力はどのようなものですか?

A:フーリエ変換の出力は、入力の可能な周波数の分布を表示するので、周波数スペクトルまたは分布と呼ばれることがあります。

Q:コンピュータはどのようにして高速フーリエ変換を計算するのですか?

A:コンピュータは高速フーリエ変換（FFT）と呼ばれるアルゴリズムを用いて、最も単純な信号の変換を除いて高速に計算します。

Q: 信号を時間軸で見ると、何がわからないのか?

A:信号を時間軸で見ても、その中にどのような音が含まれているかは分かりません。多くの信号は、周波数を分離して個別に分析することで意味を持ちます。