指数関数とは何か｜e^xの定義・性質と応用をわかりやすく解説

指数関数とは何かを初心者向けにわかりやすく解説。e^xの定義・性質から応用例まで図解で学べる入門ガイド。

著者: Leandro Alegsa

数学において、指数関数は、急速に成長する関数の一つである。より正確には、関数 exp ( x ) = e x {\exp(x)=e^{x}}である。{\displaystyle \exp(x)=e^{x}}ここで、eはオイラー定数であり、約2.71828の無理数である。 指数関数は実数全体で定義され、実数 x に対して常に正の値をとる（e^x > 0）。

定義（いくつかの見方）

  • 指数関数の標準的な定義は exp(x)=e^x。ここで e は極限 e = lim_{n→∞} (1+1/n)^n によって定義される正の定数。
  • 冪としての定義：実数 a>0 に対して a^x は、自然対数 ln を用いて a^x = e^{x\ln a} と定義できる。特に a=e のときが自然な指数関数である。
  • 級数による定義：任意の実数 x に対して次の冪級数で定義できる。exp(x)=∑_{n=0}^\infty x^n/n!。この級数は収束半径が無限大のため、すべての実数（さらに複素数）で定義される。
  • 微分方程式としての定義：y'=y、かつ y(0)=1 を満たす唯一の関数が exp(x) である。

基本的な性質

  • 指数法則：exp(a+b)=exp(a)exp(b)。これから exp(0)=1、exp(-x)=1/exp(x) などが従う。
  • 導関数と積分：d/dx exp(x)=exp(x)、∫exp(x)dx=exp(x)+C。つまり指数関数は自分自身を微分・積分する特別な関数である。
  • 単調性と凸性：exp(x) は単調増加であり、二階導関数が正なので凸関数である。
  • 極限：lim_{x→-∞} exp(x)=0、lim_{x→+∞} exp(x)=+∞。また lim_{x→0} (exp(x)-1)/x = 1。
  • 複素解析的性質：exp(x) の級数定義から、実数だけでなく複素数全体に一意に解析接続できる（全関数 = entire）。

級数展開と計算例

級数展開：exp(x)=∑_{n=0}^\infty x^n/n! = 1 + x + x^2/2! + x^3/3! + …。この級数は任意の実数 x で高速に収束するため、数値計算によく用いられる。

簡単な値の例：exp(0)=1、exp(1)=e ≈ 2.71828、exp(-1)=1/e ≈ 0.367879。

逆関数（自然対数 ln）

指数関数の逆関数は自然対数 ln(x) であり、定義域は x>0。関係式は ln(e^x)=x（すべての実 x）および e^{\ln y}=y（y>0）。微分は d/dx ln(x)=1/x となる。

底の変換と一般の指数関数

任意の正の底 a (a>0) に対する指数関数 a^x は、先に述べたように a^x = e^{x\ln a} と表せる。これにより微分や積分、極限の計算は自然対数を用いて扱える。

応用例

  • 連続複利：元金を年利 r で連続複利で運用したとき、t 年後の金額は A(t)=A_0 e^{rt} となる。
  • 人口増加モデル（単純な指数成長）：非制限な環境下での個体数は N(t)=N_0 e^{kt}（k>0）で表される。
  • 放射性崩壊や冷却などの指数減衰：量は時間とともに e^{-λt} の形で減少する（λ>0）。
  • 常微分方程式：y'=ky の一般解は y(t)=Ce^{kt}。多くの物理・工学・生物学モデルで現れる基本解である。
  • 信号処理や確率論：ガウス分布の定義や確率過程にも e^{x} が現れる。

複素数への拡張とオイラーの公式

複素数 z に対しても exp(z)=∑_{n=0}^\infty z^n/n! により定義され、オイラーの公式 exp(iθ)=cos θ + i sin θ が成り立つ。特に exp(iπ) + 1 = 0 は数学の美しい恒等式の一つである。

まとめ（注意点と指針）

  • 指数関数は級数・極限・微分方程式など複数の等価な定義を持ち、解析学や応用数学で中心的役割を果たす。
  • 計算上は exp(x) の級数や数値ライブラリの関数を用いるのが一般的で、底の変換 a^x = e^{x\ln a} に注意すると扱いやすい。
  • 指数成長は非常に速いため、現実問題に適用する際は資源制約や非線形効果（例：ロジスティック方程式）を考慮する必要がある。
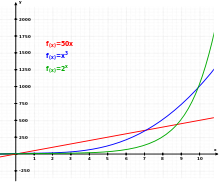
3種類の関数。リニア（赤）、キュービック（青）、エクスポネンシャル（緑）。Zoom
3種類の関数。リニア（赤）、キュービック（青）、エクスポネンシャル（緑）。

プロパティ

指数関数は指数を使用するため、同じルールに従います。したがって

exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {\exp(x+y)=\exp(x)y=e^{x+y}}.{\displaystyle \exp(x+y)=\exp(x)\exp(y)=e^{x+y}}.これは、x a・x b = x a + b {\displaystyle x^{a}\cdot x^{b}=x^{a+b}}という規則に従う。{\displaystyle x^{a}\cdot x^{b}=x^{a+b}}.

自然対数は、指数関数の逆演算です。

ln ( x ) = log e ( x ) = log ( x ) log ( e ) {\\ln(x)=\log _{e}(x)={frac {\log(x)}{\log(e)}}}。 {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}}

指数関数は、微分積分学において興味深い重要な性質を持っています。

d d x e x = e x {\frac {\mathrm {d}}e^{x}}=e^{x}}}。}{mathrm {d} x}e^{x}=e^{x}}である。｝{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}},

これは、指数関数の傾きが指数関数そのものであることを意味しており、したがって、x = {0displaystyle x=0}{\displaystyle x=0}において傾きが1であることを意味している。これらの性質は、指数関数が数学において重要な関数である理由である。

アプリケーション

指数関数は、数学関数の中でも最も有用なものの一つです。指数関数は、指数関数的な成長を表すのに使われます。指数関数的な成長は、ほぼすべての科学分野で使われており、金融分野でも顕著です。また、放射性崩壊や光の吸収のように指数関数的な減衰も起こります。

指数関数の実生活での例として、銀行の利息があります。ある人が100ポンドを月に3％の利息がつく口座に預けた場合、毎月の残高は次のようになります（お金が手つかずであると仮定した場合）。

月

バランス

月

バランス

1月

£100.00

7月

£119.41

2月

£103.00

8月

£122.99

3月

£106.09

9月

£126.68

4月

£109.27

10月

£130.48

5月

£112.55

11月

£134.39

6月

£115.93

12月

£138.42

毎月、利息による余分なお金が増えることに注目してください。元々の残高が多いほど、その人にはより多くの利息がつきます。

指数関数の2つの数学的な例を以下に示します。

a=2

x {displaystyle x}を x

結果

-2

0.25

-1

0.5

0

1

1

2

2

4

3

8

4

16

a=3

x {displaystyle x}を x

結果

-2

19

-1

13

0

1

1

3

2

9

3

27

4

81

数学定数eとの関係

基数（aa）は、10や1/2など、0より大きな数字であれば何でもいいのですが、多くの場合、eという特殊な数字になります。eは正確に書くことはできませんが、ほぼ2.71828に等しい数字です。

eという数字は、すべての指数関数にとって重要です。例えば、ある銀行が毎日0.01％の利息を支払っているとします。ある人がその利息分のお金を箱に入れておきます。1万日（約30年）後、彼は最初の2倍のお金を持っています。もう一人の人は、利子のついたお金を再び銀行に預けます。銀行は今度は彼に利子を支払うので、お金の量は指数関数になります。10,000日後、彼は最初に持っていたお金の2倍ではなく、2.718145倍のお金を持っています。この数字はeという数字に非常に近いものです。もし銀行が利息を支払う回数が増えて、毎回支払う金額が少なくなれば、この数字はeという数字に近づくことになります。

また、この絵を見ると、指数関数ではeという数字が重要であることがわかります。この絵には、3つの異なる曲線が描かれています。黒い点がある曲線は、基数がeより少し小さい指数関数です。短い黒い線がある曲線は、基数がeより少し大きい指数関数です。青い曲線は、基数がeにちょうど等しい指数関数です。赤線は青の曲線の接線で、青の曲線と交差せずに一点で接している。赤い曲線は、左から右に向かう線であるx軸を-1の位置で横切っていることがわかります。これが、eを底辺とする指数関数が特別なものである理由です。

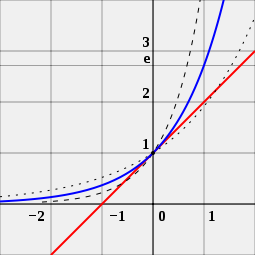
e は、指数関数f(x)=ax(青の曲線)のx=0での導関数の値がちょうど1になるような、唯一の数aです。なお、比較のために、関数2x（点線）と関数4x（破線）を示したが、これらは傾き1の直線（赤）には接していない。Zoom
e は、指数関数f(x)=ax(青の曲線)のx=0での導関数の値がちょうど1になるような、唯一の数aです。なお、比較のために、関数2x（点線）と関数4x（破線）を示したが、これらは傾き1の直線（赤）には接していない。

質問と回答

Q:指数関数とは何ですか?


A:指数関数とは、どんどん大きくなっていく数学の関数です。

Q:指数関数はどのように数学的に表現されるのですか?


A:指数関数は、exp(x) = e^xで表されます（eはオイラーの定数）。

Q:オイラー定数とは何を表しているのですか?


A:オイラー定数は、約2.71828の無理数を表します。

Q:指数関数は常に増加するのですか?


A:はい、指数関数はxが増加するにつれて常に値を増加させます。

Q:指数関数が成長する速さには限界がありますか?


A:いいえ，指数関数はxが大きくなると増加し続けるので，増加の速さに限界はありません．

Q:オイラー定数はどのように計算するのですか?


A:テイラー級数や連分数などの数値計算を用いることで、オイラー定数を算出することができます。

Q:指数関数には、数学以外にどんな応用があるのでしょうか?


A:指数関数は、物理学、化学、生物学、経済学、工学など、数学以外の分野でも多くの応用があります。


百科事典を検索する
AlegsaOnline.com - 2020 / 2025 - License CC3