微積分とは：変化と積分を扱う基礎概念と歴史

微積分とは何かをわかりやすく解説。変化の解析から積分の基礎、ニュートン・ライプニッツの歴史的発展と応用例まで初心者にも最適。

著者: Leandro Alegsa

09-01-2026 21:24

微分積分（微分積分学）は、微積分の基本概念を扱う数学の分野であり、ある変数が他の変数と比較してどのように変化するかを、関数を用いて記述・解析する学問です。極めて小さな変化を扱うことで、図形を無限に分割することなく、ある点から次の点へどのように変化するかを調べます。微分は瞬間的な変化の割合を表し、積分は量の総和や曲線下面積を求める操作であり、両者は互いに逆の関係にあります。17世紀後半、アイザック・ニュートン卿とゴットフリート・ライプニッツによってそれぞれ独立に発展し、以降は数学・自然科学の基礎理論として広く用いられてきました。

微分（導関数）とは

微分は、ある関数の入力がごく小さく変化したときに出力がどのように変化するかを示す概念です。直感的には「接線の傾き」や「瞬間の変化率」として理解できます。厳密には、点 x における関数 f の導関数 f'(x) は次の極限で定義されます。

f'(x) = lim_{h→0} (f(x+h) − f(x)) / h

微分の基本的な計算法則には、合成関数の微分（連鎖律）、積・商の微分法則、冪関数や指数関数・対数関数の微分などがあります。微分は物理学の速度や加速度、経済学の限界変化、工学の最適化問題などで重要な役割を果たします。

積分とは

積分は、関数の値を基にして「総量」を求める手法です。最も基本的な意味では、曲線 y = f(x) と x 軸で囲まれた部分の面積（定積分）を表します。定積分は区間 [a, b] における極限和（リーマン和）として定義され、次のように表されます。

∫_a^b f(x) dx = lim (分割幅→0) Σ f(x_i*) Δx_i

不定積分（原始関数）は、ある関数の導関数が元の関数になるような関数の全体を指します。積分計算には置換積分、部分積分、部分分数分解などの手法があり、微分方程式の解法や面積・体積の計算、累積量の評価に用いられます。

微分と積分を結ぶ基本定理

微積分学の基本定理は、微分と積分が互いに逆の操作であることを示します。具体的には、適切な条件の下で、(1) 関数の原始関数の導関数は元の関数に等しいこと、(2) 定積分は原始関数の値の差で与えられること、が成り立ちます。この定理があるために、積分計算は多くの場合、原始関数を求めることで実行できます。

厳密化と歴史的発展

ニュートンとライプニッツは独自の視点で微分積分の直感的手法を構築しましたが、19世紀には極限の概念を用いた厳密な定義が整えられました。コーシーやワイエルシュトラスらにより、ε–δ論法を使った厳密化が行われ、解析学の基礎が固められました。20世紀には非標準解析（超準解析）など、無限小量を再び形式的に扱う試みも登場しています。

主な応用例

物理学：運動の記述（速度・加速度）、力学、電磁気学、波動・熱伝導方程式の解析
工学：制御理論、信号処理、構造解析、最適化
経済学・金融：最適化問題、消費・生産の限界分析、連続時間モデル
生命科学・統計学：集団モデル（微分方程式）、確率過程の解析

学習のポイント

極限と連続性の理解を優先すること（微分積分の基礎となる）
導関数と原始関数（不定積分）の計算法を段階的に身につけること
基本定理を使った定積分計算と数値積分の考え方を学ぶこと
微分方程式の初歩（一次の線形常微分方程式など）に触れて応用力を養うこと

微分積分は概念的には単純に「変化」と「蓄積」を扱う道具ですが、その応用範囲は極めて広く、科学技術や社会科学の多くの分野で必須の基礎知識となっています。

背景

5や200といった数字とは異なり、変数はその値を変えることができる。例えば、距離と時間は変数である。オリンピックの徒競走では、走れば走るほど、スタートラインからの距離が伸びていきます。一方、ストップウォッチや時計は、上がるにつれて時間を計測します。走った距離を時間で割れば、そのランナーの平均的なスピードが測れる。しかし、これでは、その人がちょうど1.5秒後にどのような速度で走っていたのかがわかりません。もし、1秒後の距離と2秒後の距離があったとしても、レース全体の平均よりは正しいかもしれませんが、やはり平均しか出てきません。

微積分が発明されるまで、これを計算する唯一の方法は、時間をどんどん小さく切って、小さい時間の平均速度がちょうど1.5秒の実際の速度に近づいていくようにすることであった。これは非常に長く大変な作業で、人々が何かを解決しようとするたびに行わなければならなかった。スピードメーターを持たず、オドメーター（距離計）と時計だけで車の速度を割り出そうとするドライバーを想像してみてください。

よく似た問題に、曲線上の任意の点での傾き（どの程度急か）を求めるものがある。直線の傾きは、単純に、どれだけ上るか（yまたは垂直方向）をどれだけ横切るか（xまたは水平方向）で割ったものである。線がx軸に平行であれば、その傾きはゼロである。直線が (x,y) = (2,10) と (4,18) を通る場合、線は 8 上がって 2 横切るので、傾きは 8 割る 2 で 4 となる。

しかし、「曲線」では、線が曲がっているため、傾きは可変である（点によって異なる値を持つ）。しかし、曲線を非常に細かく切り分けた場合、その点での曲線はほとんど短い直線のように見えるだろう。そこで、その傾きを求めるには、その点を通る、その点での曲線と同じ傾きの直線を描けばよい。この直線の傾きが曲線と同じであれば、接線と呼ばれる。しかし、その接線が正確にできているかどうかは（微積分をしなければ）わからない。また、私たちの目は、それが正確なのか、それとも単に非常に近いのかを確かめるほど正確ではない。

ニュートンとライプニッツが発見したのは、単純で論理的なルールで傾き（距離の例では速度）を正確に計算する方法であった。彼らは、曲線を非常に小さな断片に無限に分割した。そして、興味のある点の両側にある点を選び、それぞれで接線を計算した。その接線が曲線の実際の傾きに近づくにつれて、傾きはある特定の値に近づいた。彼らは、この近づいてきた特定の値こそが、実際の傾きであると言った。

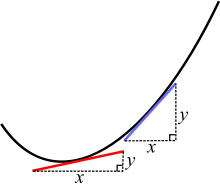
曲線上では、異なる2点は異なる傾きを持つ。赤と青の線は、曲線の接線である。

仕組み

fはfunctionの略ですから、この式は「yはxの関数である」という意味になります。これは、yが縦軸のどの高さにあるかは、その時のx（横軸）が何であるかに依存することを表しています。例えば、y = x²という方程式では、xが1ならyは1、xが3ならyは9、xが20ならyは400になることが分かります。

次に、曲線上の点Aを選び、その水平位置をxと呼ぶ。そして、Aより少し横に離れた別の点Bを選び、その水平位置をx＋hと呼ぶ。

そこで、A点からB点に行くとき、縦の位置はf(x)からf(x + h)に、横の位置はxからx + hになったことになります。ですから、傾きは次のようになります。

f ( x + h ) - f ( x ) h {displaystyle {frac {f(x+h)-f(x)}{h}} }. ${\frac {f(x+h)-f(x)}{h}}$

BをAに近づければ、つまりhが0に近づけば、A点での傾きを知ることに近づく。

lim h → 0 f ( x + h ) - f ( x ) h { {displaystyle \lim _{highedarrow 0}{frac {f(x+h)-f(x)}{h}}}} { {frac {f(x+h)-f(x)}{h}}} { {displaystyle &#89847 $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

さて、y = x²に戻ろう。これの傾きは、次のように求めることができる。

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {displaystyle {begin{aligned}& ...=lim _{h}rightarrow 0}{hfrac {f(x+h)-f(x)}{h}}}&=lim _{h}rightarrow 0}{frac {(x+h)^{2}-(x)^{2}}{h}} end{aligned}}} {=lim _{h}rightarrow 0}{h}rightalow {h}{h}{h}{h}}{h}&=im {h}{h}{h}{h}{h}{h}{h}{h}} {h}<h ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

( x + y ) 2 = x 2 + 2 x y + y 2 {displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ となる二項定理を適用すると、以下のように還元できる。

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {displaystyle { {begin{aligned}&=lim _{h}rightarrow 0}{hfrac {x^{2}+2xh+h^{2}-x^{2}}{h}}&=lim _{h}rightarrow 0}{hfrac {2xh+h^{2}}{h}}&=lim _{h}rightarrow 0}2x+h}&={hfrac {}{}2x}end{aligned}}}=lim _{h}ライトアロー ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

つまり、曲線 f(x) = x² 上のどの点でも、微分 f'(x) (アポストロフィのマーク) は 2x になることが、接線を引くまでもなくわかるのです。このように極限を使って傾きを求めることを微分と呼ぶ．

ライプニッツは同じ結果を得たが、hを「dx」と呼び、「xの微量な変化」を意味した。ライプニッツは、その結果生じるf(x)の変化を「dy」と呼び、これは「微量のy」を意味する。ライプニッツの表記法がより多くの書籍で使われているのは、方程式が複雑になったときに理解しやすいからである。ライプニッツ記法では

d y d x = f ′ ( x ) {displaystyle {frac {dy}{dx}}=f'(x)} }. ${\frac {dy}{dx}}=f'(x)$

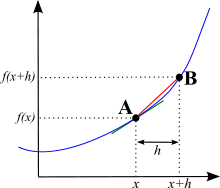
曲線上のxとx＋hが何を意味するかを示す絵。

ルール

このようなシステムを用いて、数学者はどのような関数を見ても、常に有効な規則を作り出したのである。(注: ここでは、u {displaystyle u} $u$ と v {displaystyle v} $v$ は両方とも x {displaystyle x} の関数である)

コンディション	機能	デリバティブ	例	デリバティブ
単体での数値	y = a {displaystyle y=a} $y=a$	d y d x = 0 {displaystyle {frac {dy}{dx}=0}}. ${\frac {dy}{dx}}=0$	y = 3 {displaystyle y=3}. $y=3$	0 {displaystyle 0｝ $0$
直線	y = m x + c {displaystyle y=mx+c} $y=mx+c$	d y d x = m {displaystyle {frac {dy}{dx}}=m｝ ${\frac {dy}{dx}}=m$	y = 3 x + 5 {displaystyle y=3x+5}. $y=3x+5$	3} {displaystyle 3 $3$
xの累乗	x a {displaystyle x^{a}} $x^{a}$	d y d x = a x a - 1 {displaystyle { {frac {dy}{dx}}=ax^{a-1}}}. ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {displaystyle x^{12}}} $x^{12}$	12 x 11 {displaystyle 12x^{11}}}. $12x^{11}$
関数で掛け合わせた数値	y = c ⋅ u {displaystyle y=carette u} $y=c\cdot u$	d y d x = c d u d x {displaystyle {}{dy}{dx}}=c{frac {du}{dx}}}. ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {displaystyle y=3(x^{2}+x)}. $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {displaystyle 3(2x+1) } {displaystyle 3(2x+1) }. $3(2x+1)$
機能＋αの機能	y = u + v {displaystyle y=u+v} $y=u+v$	d y d x = d u d x + d v d x {displaystyle {{frac {dy}{dx}}={{frac {du}{dx}}+{frac {dv}{dx}}}}. ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {displaystyle y=3x^{2}+{hatsqrt {x}}}. $y=3x^{2}+{\sqrt {x}}$	6 x + 1 x {displaystyle 6x+{Cfrac {1}{sqrt {x}}}}. $6x+{\frac {1}{\sqrt {x}}}$
関数から別の関数を引いたもの	y = u - v {displaystyle y=u-v} $y=u-v$	d y d x = d u d x - d v d x {displaystyle { {frac {dy}{dx}}={frac {du}{dx}}-{frac {dv}{dx}}}}. ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {displaystyle y=3x^{2}-{hatsqrt {x}}}. $y=3x^{2}-{\sqrt {x}}$	6 x - 1 x {displaystyle 6x-{Afrac {1}{sqrt {x}}}}. $6x-{\frac {1}{\sqrt {x}}}$
積の法則関数と他の関数を掛け合わせたもの	y = u ⋅ v {displaystyle y=ucdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {displaystyle {}={Chefrac {du}{dx}}v+u{Chefrac {dv}{dx}}}}. ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {displaystyle y=(x^{2}+x+2)(3x-1)} {displaystyle y=(x^{2}+x+2)(3x-1) $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)} } {displaystyle (3x-1)(2x+1)+3(x^{2}+x+2) $(3x-1)(2x+1)+3(x^{2}+x+2)$
商法則関数を別の関数で割ったもの	y = u v {displaystyle y={{frac {u}{v}}}}. $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {displaystyle { {frac {dy}{dx}}={frac {{frac {du}{dx}}v-u{frac {dv}{dx}}}{v^{2}}}} {displaystyle { {frac {du}{dx}}v-u {frac {dv}{dx}}}{v^{2}}} {displaystyle {frac {dx}={frac ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {displaystyle y={{frac {x^{2}+2}{x-1}}}}. $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {displaystyle {} {frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}}}. ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
鎖の法則複合関数に使用	y = u ∘ v {displaystyle y=ucirc v}. $y=u\circ v$	d y d x = d y d u ⋅ d u d x {displaystyle {} {{frac {dy}{dx}}={}frac {dy}{du}} {cdot {}frac {du}{dx}}}}. ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {displaystyle y={CASQRT {2x-1}}}. $y={\sqrt {2x-1}}$	2 2 x - 1 = 1 2 x - 1 {displaystyle {{Cfrac {2}{2{Cathqrt {2x-1}}}={Cfrac {1}{Cathqrt {2x-1}}}}}}}. ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
指数関数	y = e x {displaystyle {}y=e^{x}}. ${\frac {}{}}y=e^{x}$	d y d x = e x {displaystyle {frac {dy}{dx}}=e^{x}}. ${\frac {dy}{dx}}=e^{x}$	y = e x {displaystyle {}y=e^{x}}. ${\frac {}{}}y=e^{x}$	e x {displaystyle}{frac}{}e^{x}}。 ${\frac {}{}}e^{x}$