黄金比
1つの数aともう1つの小さい数bの場合，2つの数を割ることで2つの数の比を求めることができる．その比は a/b である．もう一つの比率は，2つの数a+bを足して，これを大きい方の数aで割ることによって求められる．この２つの比率が同じ数に等しい場合、その数は黄金比と呼ばれる。ギリシア文字のφは
(ファイ)は通常、黄金比の名称として用いられる。
例えば、b=1でa/b=φ{\displaystyle \varphi }の場合。♪ then a = φ {displaystyle ¶varphi } ♪ then a = φ {displaystyle ¶varphi.第２の比率(a+b)/aは、( φ + 1 )/φ {\displaystyle (\varphi +1)/\varphi }となる。
.この2つの比率は等しいので、これは真実です。
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}}}}}}}}}。
この数字の書き方の一つは
φ = 1 + 5 2 {\displaystyle ﾞVarphi ={\frac {1+{\sqrt {5}}}{2}}}}}}}}}}}}}}}}}}}}}
5 {\displaystyle {Sqrt {5}}} 
is like any number which is like, when multip multip multip multiped by itself, makes 5 (or which number is multiped): 5 × 5 = 5 {\displaystyle {\sqrt {5}times {\sqrt {5}}=5
} .
黄金比は不合理な数字です。人が書こうとすると、決して止まることなく、パターン化することなく、このように始まります：1.6180339887...この数の重要な点は、人はそこから1を引くことができるか、1をそれで割ることができるということです。どちらにしても、この数字はずっと進み続け、止まることはありません。
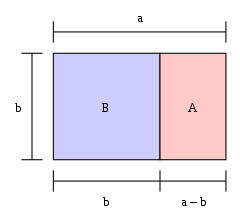
金色の長方形
長方形の長さをその幅で割ったものが黄金比に等しい場合、その長方形は「黄金の長方形」となります。黄金の長方形の一端から四角形を切り取った場合、もう一方の端は新たな黄金の長方形となります。図では、大きな長方形（青とピンクを合わせたもの）は、a / b = φ {\displaystyle a/b=\varphi }なので、黄金の長方形になります。
.青色の部分（B）は正方形である。ピンクの部分(A)は金色の四角形だから b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi }
.大きな四角形とピンクの四角形は同じ形をしていますが、ピンクの四角形の方が小さくて回転しています。
大きな四角形BAは金色の四角形であり、比率b:aは1:φ{\displaystyle varphi }である。.そのような長方形について、そして、その特定の比率の長方形についてのみ、四角いBを取り除くと、残されたのは、もう一つの金色の長方形、Aである。
フィボナッチすう
フィボナッチ数の数字の羅列です。人は、最後の2つの数字を一緒に追加することによって、リスト内の次の数を見つけることができます。人がリストの中の数字をその前に来た数字で割ると、この比率は黄金比に近づいてきます。
| フィボナッチすう | 割り算 | 割合 |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| ♪ φ {pos(100,000)} } | = 1.6180... |
自然界の黄金比
自然界では、葉や花の配置に黄金比がよく使われています。これらは、約137.5度の黄金角度を使用しています。この角度に配置された葉や花は、最高の日光を使用しています。
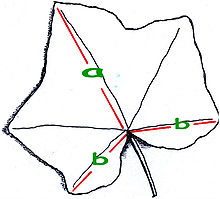
黄金比を示す一般的なツタの葉
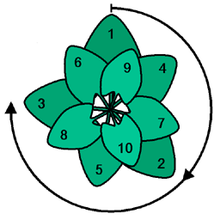
黄金の角度を使うことで、太陽の光を最適に利用することができます。上から見た様子です。
質問と回答
Q:2つの数の比は何ですか?
A:2つの数の比は、それらを割ることによって求められるので、比はa/bとなる。
Q:別の比率はどのように見つけることができますか?
A:別の比率は、2つの数を足し、その合計を大きい方の数aで割ることによって求めることができます。
Q:これらの2つの比が互いに等しいときの名称は何ですか?
A:これらの2つの比率が互いに等しいとき、それは黄金比と呼ばれます。通常、ギリシャ文字צまたはΦで表される。
Q:もしb＝1でa／b＝צなら、aはどうなるのか?
A:もしb = 1でa/b = צなら、同様にa = צということになる。
Q:この数はどのように書けばよいのでしょうか?
A:この数字を書く一つの方法は、צ = 1 + 5 / 2 = 1.618...です。
Q:そこから1を引いたり、1で割ったりすると、どういう意味になりますか?
A:そこから1を引いたり、1で割ったりすると、同じ数、つまり、どちらも黄金比に等しい数が返ってくるのです。
Q:黄金比は不合理数ですか?
A:はい、黄金比は無理数です。つまり、誰かがそれを書き出そうとすると、決して終わりやパターンがないのです。
